Index of Refraction - Definition, Examples, Quiz, FAQ, Trivia
Discover how light bends when moving between different materials!
What is Refractive Index?
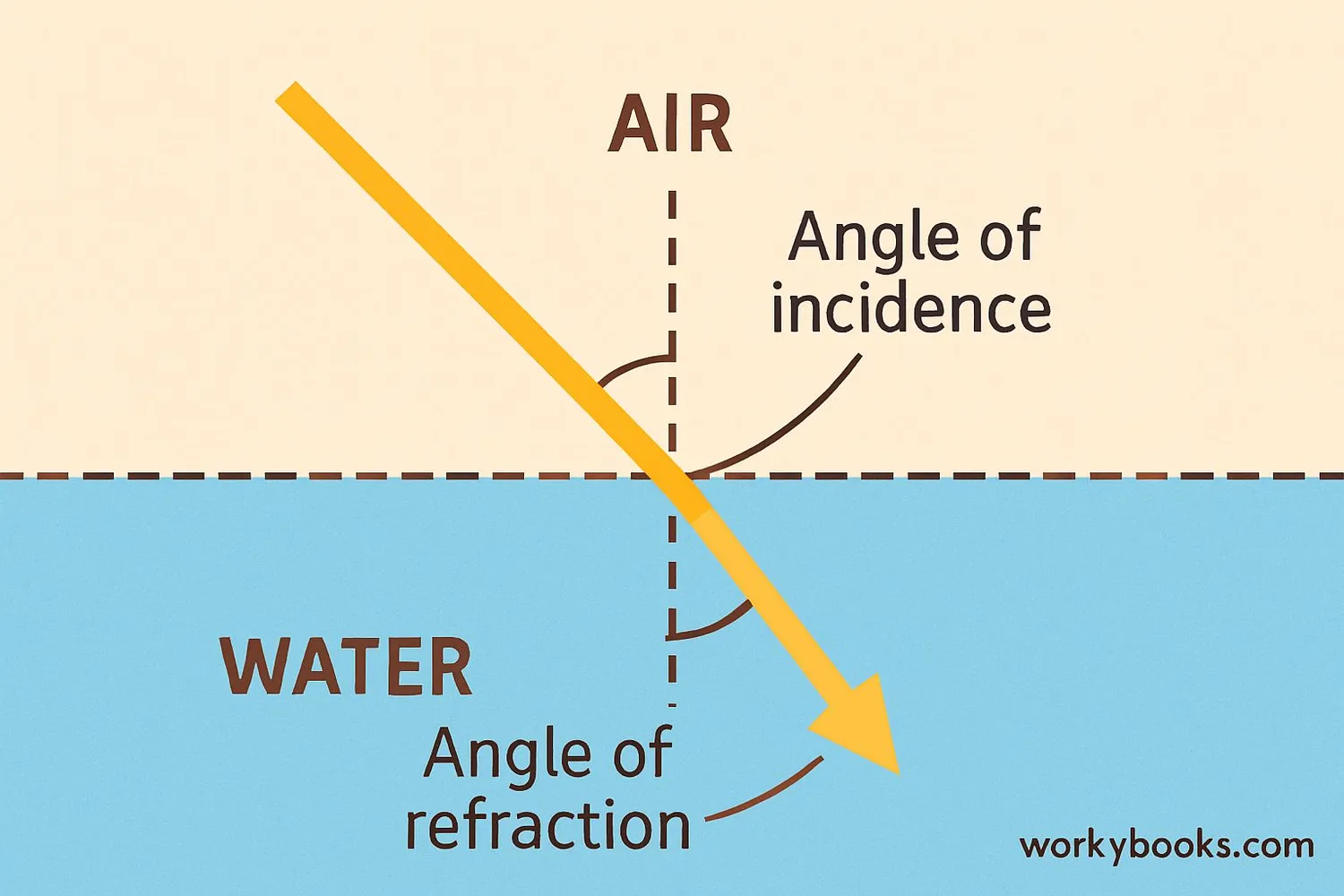
The index of refraction (also called refractive index) measures how much light bends, or refracts, when it enters a material. It tells us how much slower light travels in a material compared to its speed in a vacuum.
Think of it like this: when you run on pavement, you can move quickly. But when you enter water at the beach, you slow down. Light behaves similarly! When it moves from air (fast) into water (slower), it changes direction. This bending is called refraction.
Key Definition
Refractive Index (n) = Speed of Light in Vacuum / Speed of Light in Material
The refractive index of a vacuum is exactly 1. Air has a refractive index very close to 1 (approximately 1.0003). Water has a refractive index of about 1.33, which means light travels about 1.33 times slower in water than in a vacuum.
How to Calculate Refractive Index
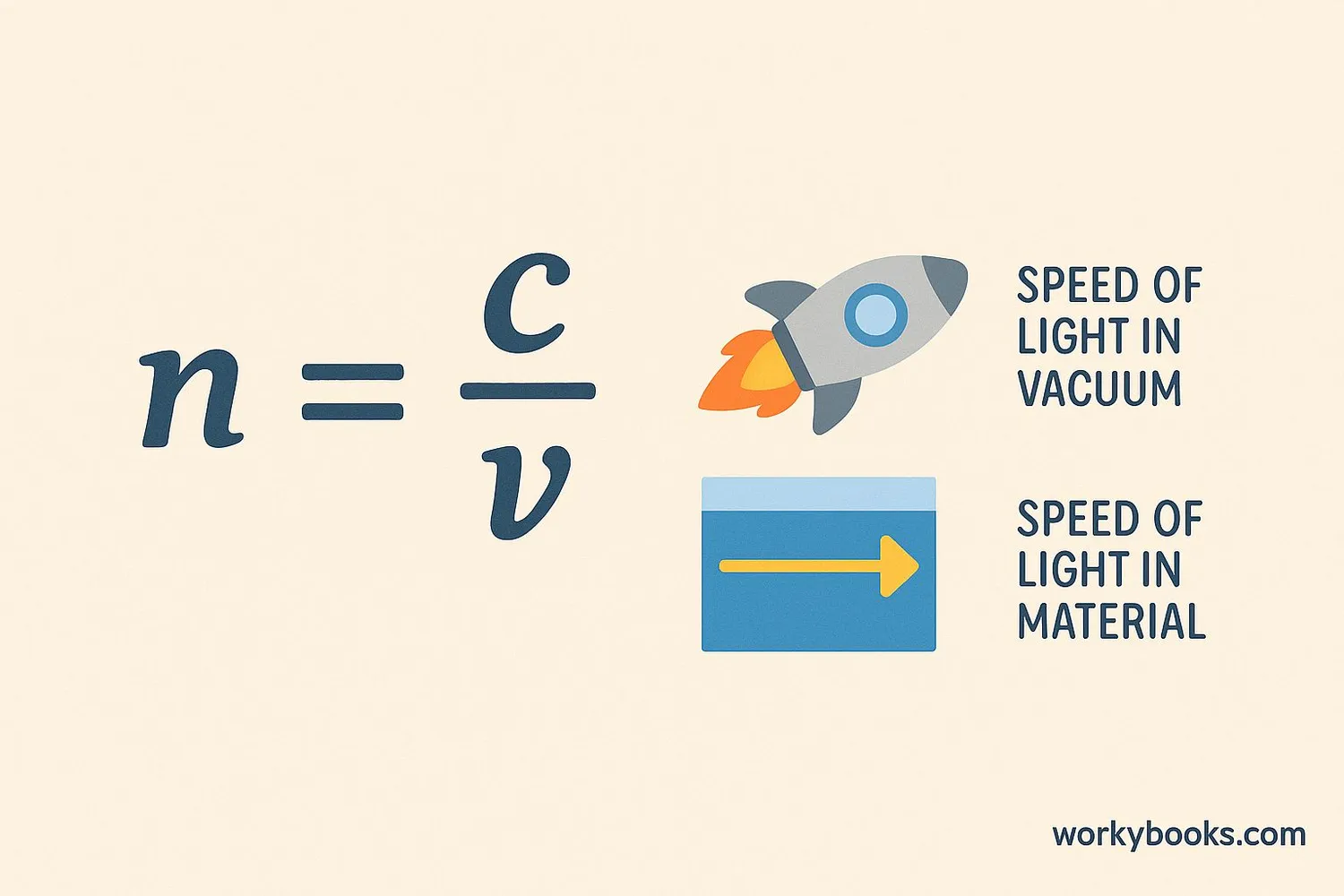
Calculating refractive index is straightforward using this formula:
n = c / v
Where:
• n is the refractive index
• c is the speed of light in a vacuum (300,000 km/s)
• v is the speed of light in the material
Measure Speed
Determine the speed of light in the material
Apply Formula
Divide speed in vacuum by speed in material
Get Result
The quotient is the refractive index
Example Calculation
For water, light travels at 225,000 km/s. So n = 300,000 / 225,000 = 1.33
Refractive Index of Common Materials
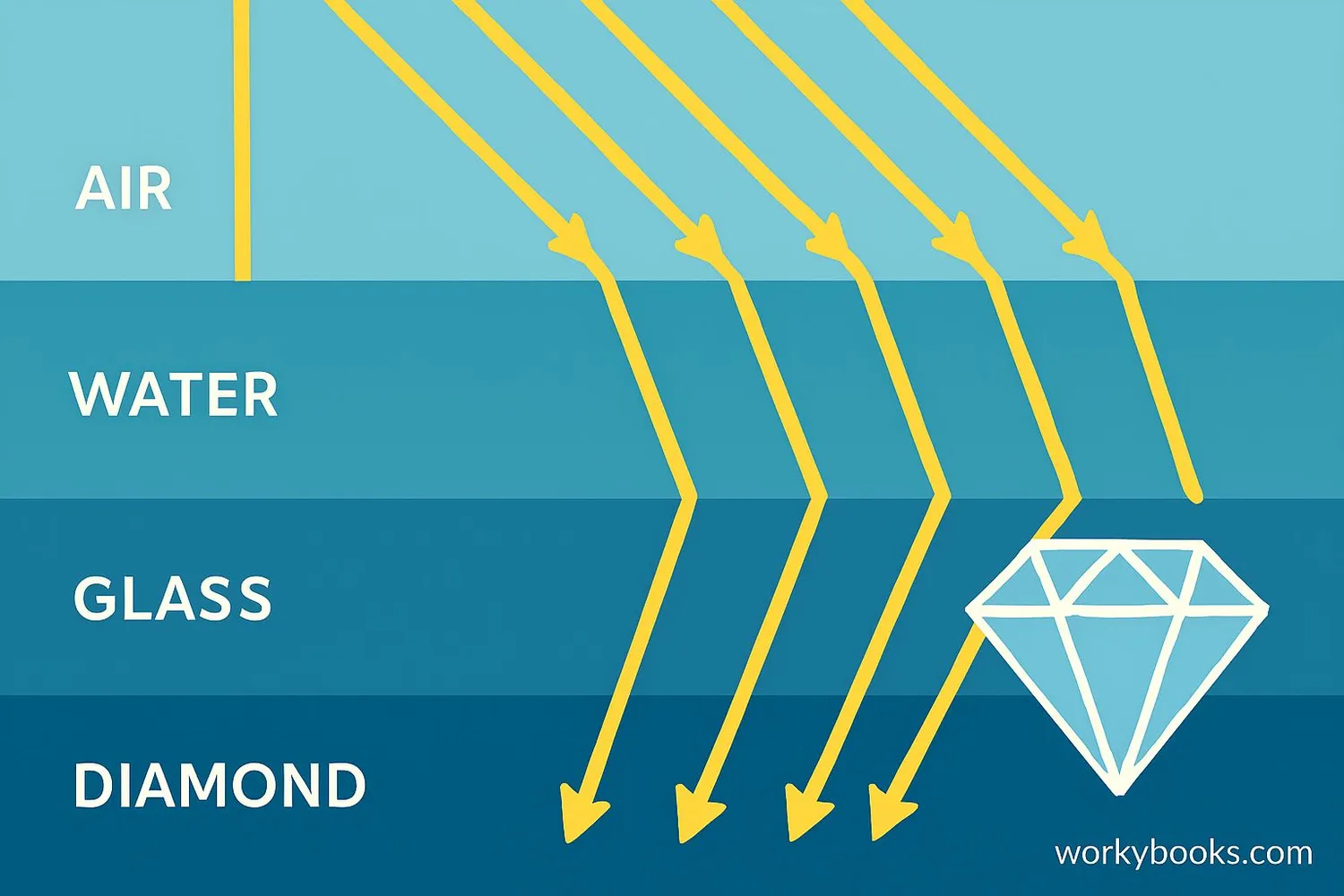
Different materials have different refractive indices. Here are some common examples:
| Material | Refractive Index | Example of Use |
|---|---|---|
| Air | 1.0003 | Our atmosphere |
| Water | 1.33 | Swimming pools, lenses |
| Glass | 1.52 | Windows, eyeglasses |
| Diamond | 2.42 | Jewelry |
| Plastic (acrylic) | 1.49 | Optical fibers, displays |
Did You Know?
Diamonds sparkle because they have a high refractive index, which causes light to bend significantly and reflect internally many times before exiting.
Snell's Law and Light Refraction
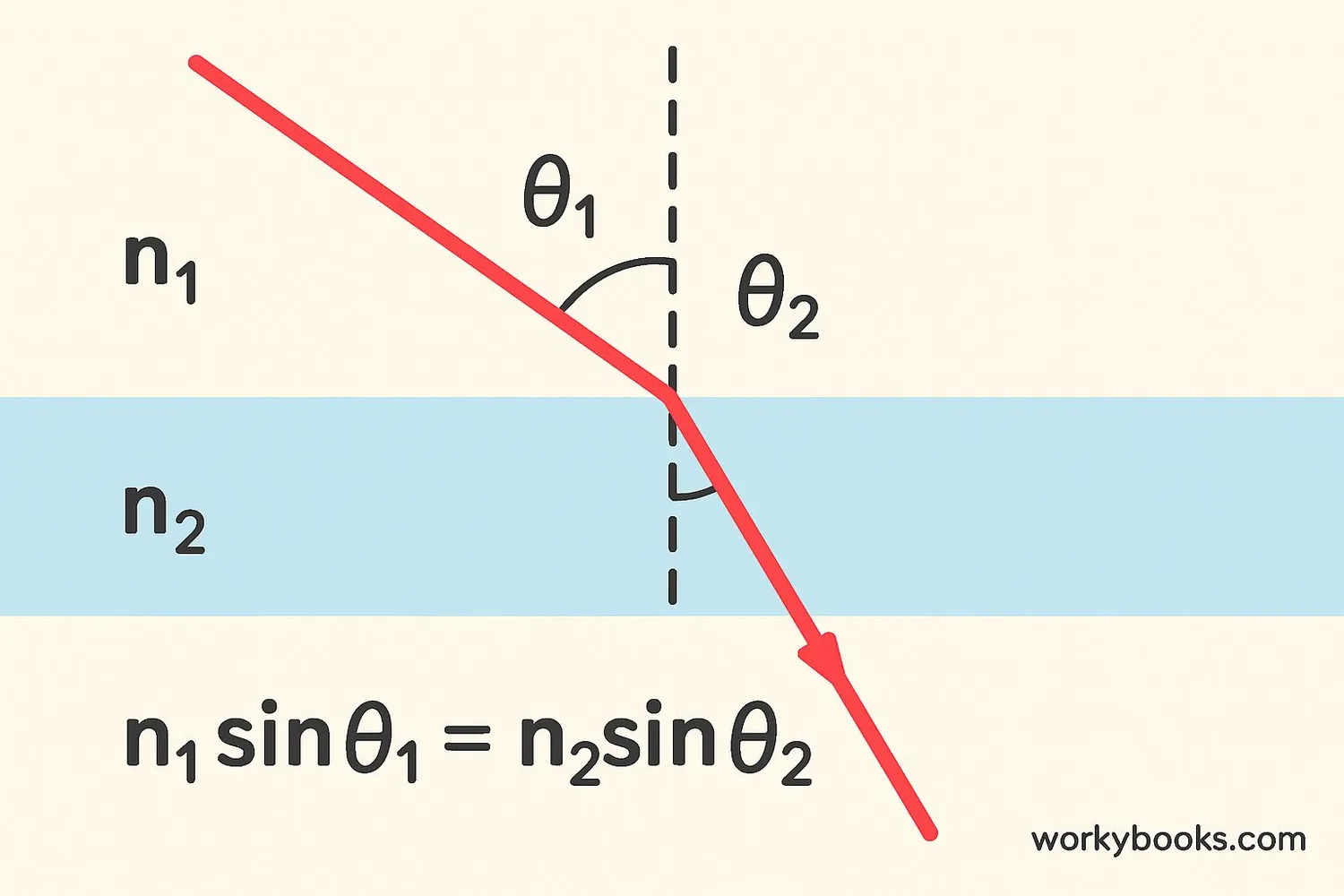
Snell's Law mathematically describes how light bends when moving between materials with different refractive indices. The law is named after Dutch mathematician Willebrord Snellius.
The formula for Snell's Law is:
n₁sinθ₁ = n₂sinθ₂
Where:
• n₁ and n₂ are the refractive indices of the two materials
• θ₁ is the angle of incidence (angle between incoming light and perpendicular line)
• θ₂ is the angle of refraction (angle between refracted light and perpendicular line)
Light Bending Direction
When light enters a material with higher refractive index, it bends toward the normal line
Reverse Direction
When light exits to a material with lower refractive index, it bends away from the normal line
No Bending
If light enters perpendicular to the surface (along the normal), it doesn't bend at all
Applications of Refractive Index

Understanding refractive index has many practical applications in our daily lives and technology:
Lenses
Eyeglasses, cameras, and microscopes use curved lenses that bend light to focus images
Prisms
Prisms use refraction to separate white light into its colorful components (rainbow)
Fiber Optics
Optical fibers use total internal reflection to transmit data as light signals
Other important applications include:
• Mirages - caused by light bending through air layers of different temperatures
• Gemstone identification - jewelers use refractive index to identify gems
• Anti-reflective coatings - reduce glare on glasses and camera lenses
• Rainbows - formed by refraction and reflection in water droplets
Refractive Index Quiz
Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned about refractive index.
Frequently Asked Questions
Here are answers to some common questions about refractive index:
Interesting Facts About Refractive Index
Discover some amazing facts about refractive index and light bending!
Animal Vision
Some animals, like the mantis shrimp, can see polarized light because their eyes contain materials with unique refractive properties that filter light in special ways.
Gravitational Lensing
Massive objects in space, like galaxies, can bend light due to gravity—an effect similar to refraction called gravitational lensing, which helps astronomers study distant objects.
Invisibility Research
Scientists are developing metamaterials with negative refractive indices that could potentially bend light around objects, making them invisible to the human eye.
Ancient Understanding
The Romans may have understood refraction principles—they created the first glass spheres filled with water to magnify objects, using the refractive properties of water and glass.





