30-60-90 Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn the special properties of 30-60-90 triangles with easy explanations and practice activities
What is a 30-60-90 Triangle?
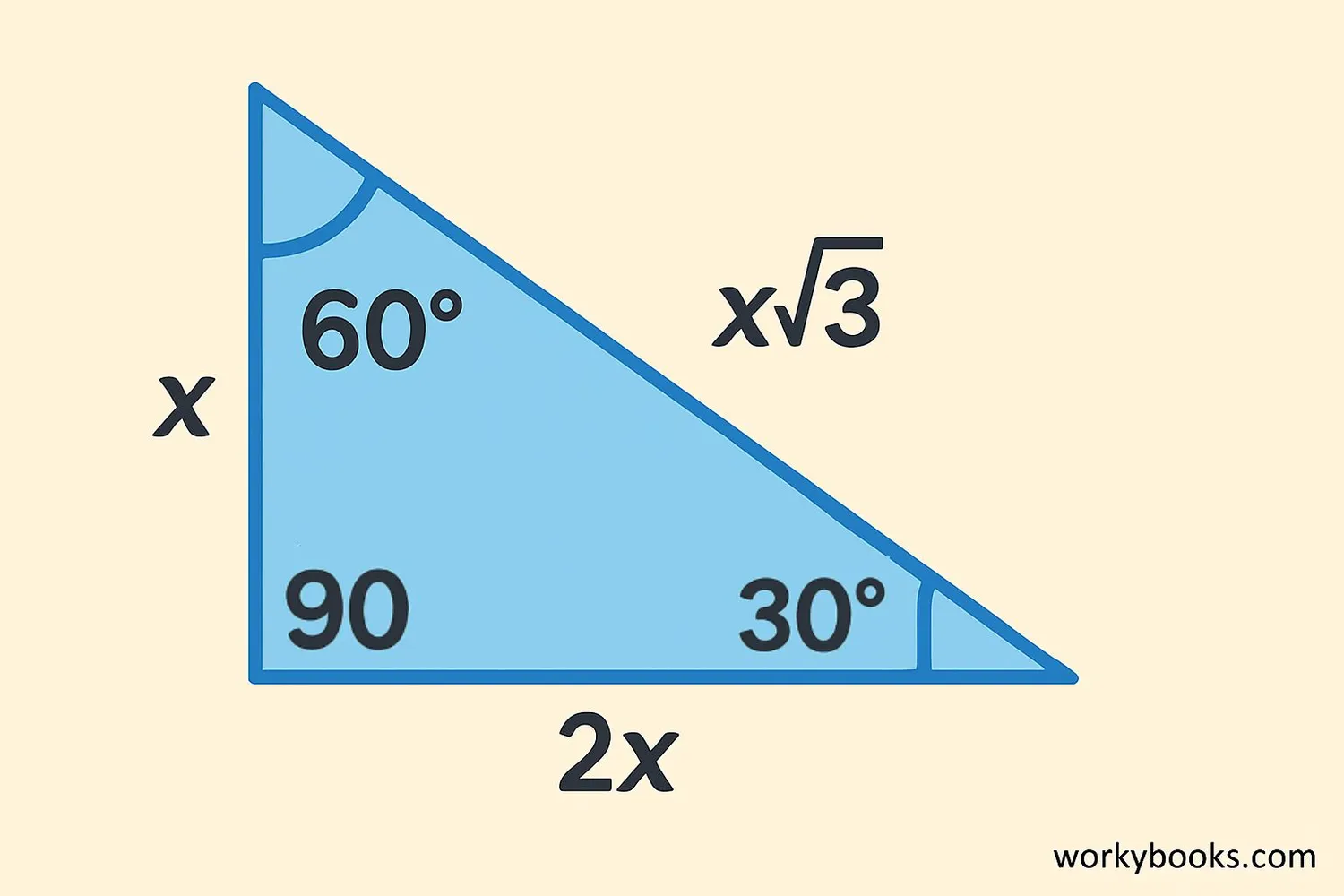
A 30-60-90 triangle is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees.
What makes it special? The sides always have a consistent relationship! If you know the length of one side, you can find the lengths of the other two sides using a simple ratio. This makes solving problems with 30-60-90 triangles much easier than with other triangles.
These triangles are called "special right triangles" because of their predictable side ratios. They appear frequently in geometry, trigonometry, architecture, and engineering.
Key Concept
In every 30-60-90 triangle, the sides are in the ratio 1 : √3 : 2
Properties & Formula
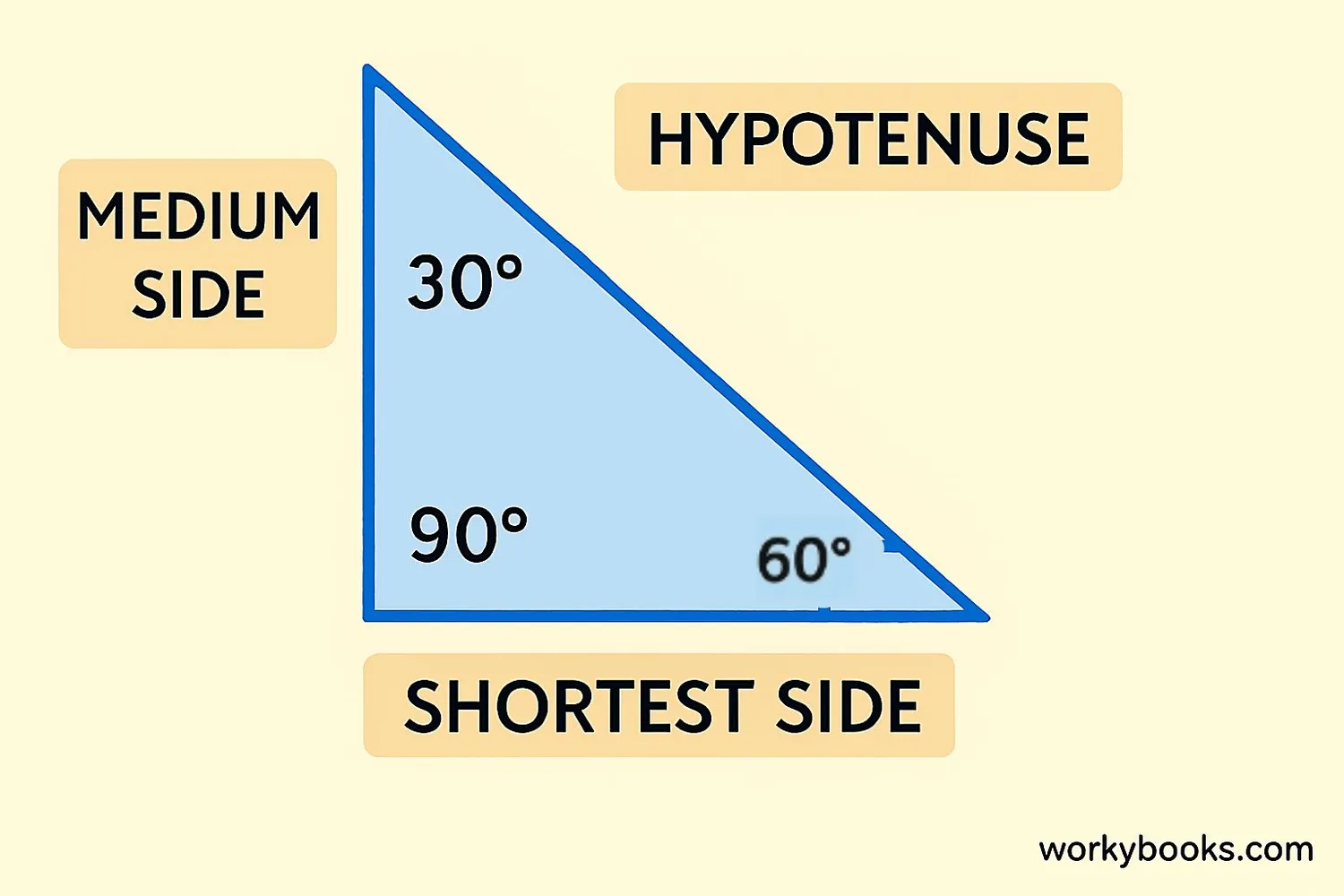
The 30-60-90 triangle has a consistent side ratio that makes calculations easy. Here's how it works:
30-60-90 Triangle Ratio
This ratio represents the sides opposite to the angles:
- Side opposite 30° angle: x
- Side opposite 60° angle: x√3
- Hypotenuse (opposite 90°): 2x
- The shortest side is always opposite the 30° angle
- The side opposite the 60° angle is √3 times the shortest side
- The hypotenuse is twice the shortest side
Remember
The hypotenuse is always the longest side in any right triangle. In a 30-60-90 triangle, it's exactly twice as long as the shortest side.
Examples & Problems
Let's solve some problems using the 30-60-90 triangle properties:
Example 1: If the shortest side (opposite 30°) is 4 cm, find the other sides.
Solution:
- Side opposite 60° = 4 × √3 ≈ 4 × 1.732 = 6.928 cm
- Hypotenuse = 2 × 4 = 8 cm
Example 2: If the hypotenuse is 12 cm, find the other sides.
Solution:
- Shortest side (opposite 30°) = hypotenuse ÷ 2 = 12 ÷ 2 = 6 cm
- Side opposite 60° = 6 × √3 ≈ 6 × 1.732 = 10.392 cm
Example 3: If the side opposite 60° is 9 cm, find the other sides.
Solution:
- Shortest side = (side opposite 60°) ÷ √3 = 9 ÷ √3 ≈ 9 ÷ 1.732 ≈ 5.196 cm
- Hypotenuse = 2 × shortest side ≈ 2 × 5.196 = 10.392 cm
Practice solving these types of problems to master 30-60-90 triangles!
Problem Solving Tip
Always start by identifying which side you know and which angle it's opposite to. Then use the ratio to find the other sides.
Practice Quiz
Test your understanding of 30-60-90 triangles with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about 30-60-90 triangles:
Math Trivia
Discover interesting facts about triangles and geometry:
Ancient Geometry
The properties of special triangles were known to ancient Egyptian and Babylonian mathematicians over 4000 years ago. They used these relationships to build pyramids and survey land.
Triangle Strength
Triangles are the strongest geometric shape because their fixed angles distribute force evenly. This is why you see triangles in bridges, roof trusses, and bicycle frames.
Space Navigation
NASA engineers use trigonometry with special triangles to calculate spacecraft trajectories. The Apollo missions to the Moon relied on these mathematical principles.
Triangle in Nature
Honeybees build honeycombs with hexagonal cells, which are made up of many triangular shapes. This efficient structure uses the least amount of wax to store the most honey.


