Associative Property - Definition, Examples, Quiz, FAQ, Trivia
Learn how grouping numbers doesn't change the result in addition and multiplication
What is the Associative Property?
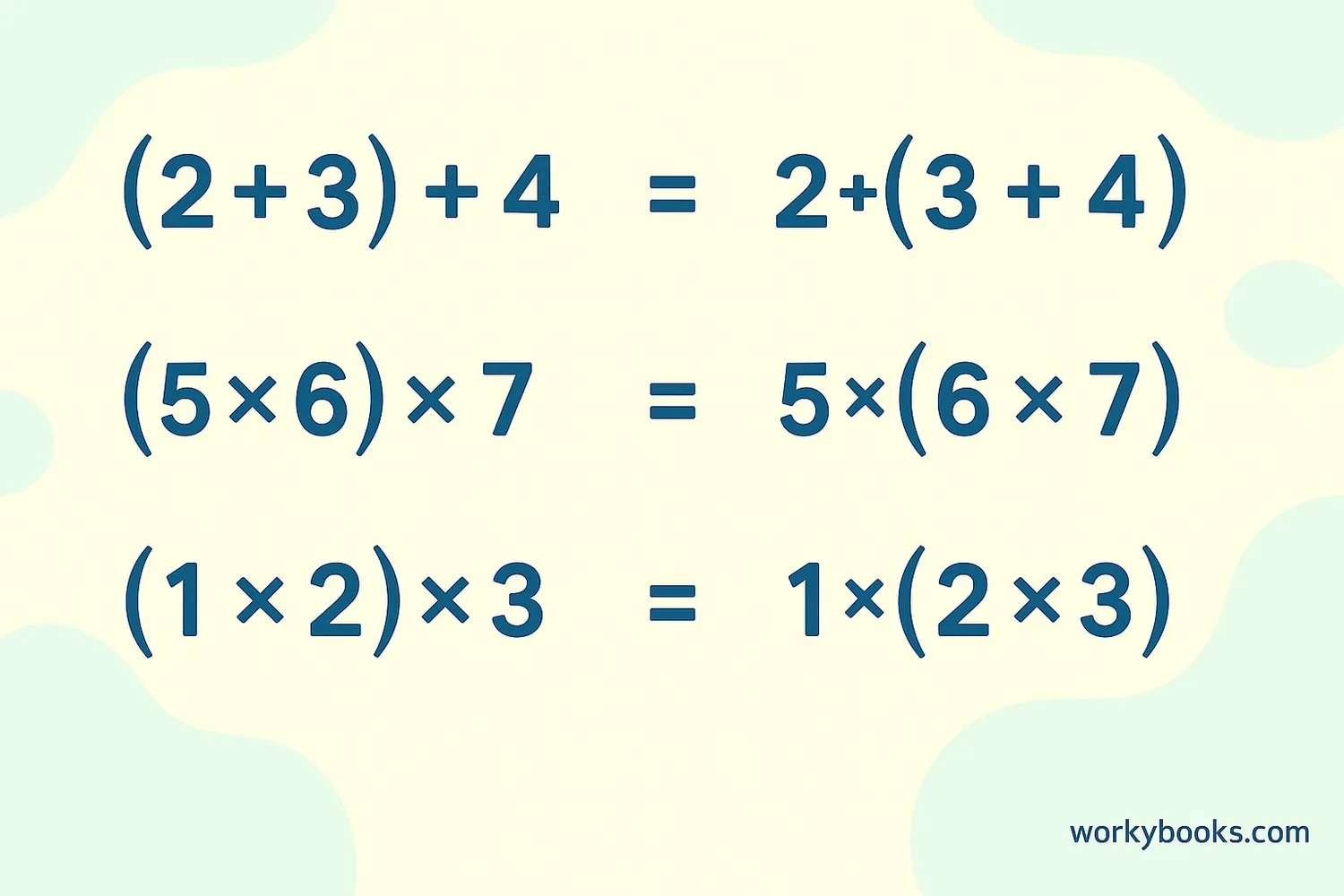
The associative property is a math rule that tells us we can group numbers in different ways when adding or multiplying without changing the result. It's all about where we put the parentheses!
The associative property says that when we are only adding or only multiplying, we can change the grouping of the numbers and still get the same answer.
This property is important because it gives us flexibility in how we solve problems. It helps us simplify calculations and solve equations more easily.
Key Concept
Associative Property applies only to addition and multiplication. It does NOT work for subtraction or division.
General Formula
(a × b) × c = a × (b × c) (Multiplication)
Associative Property of Addition
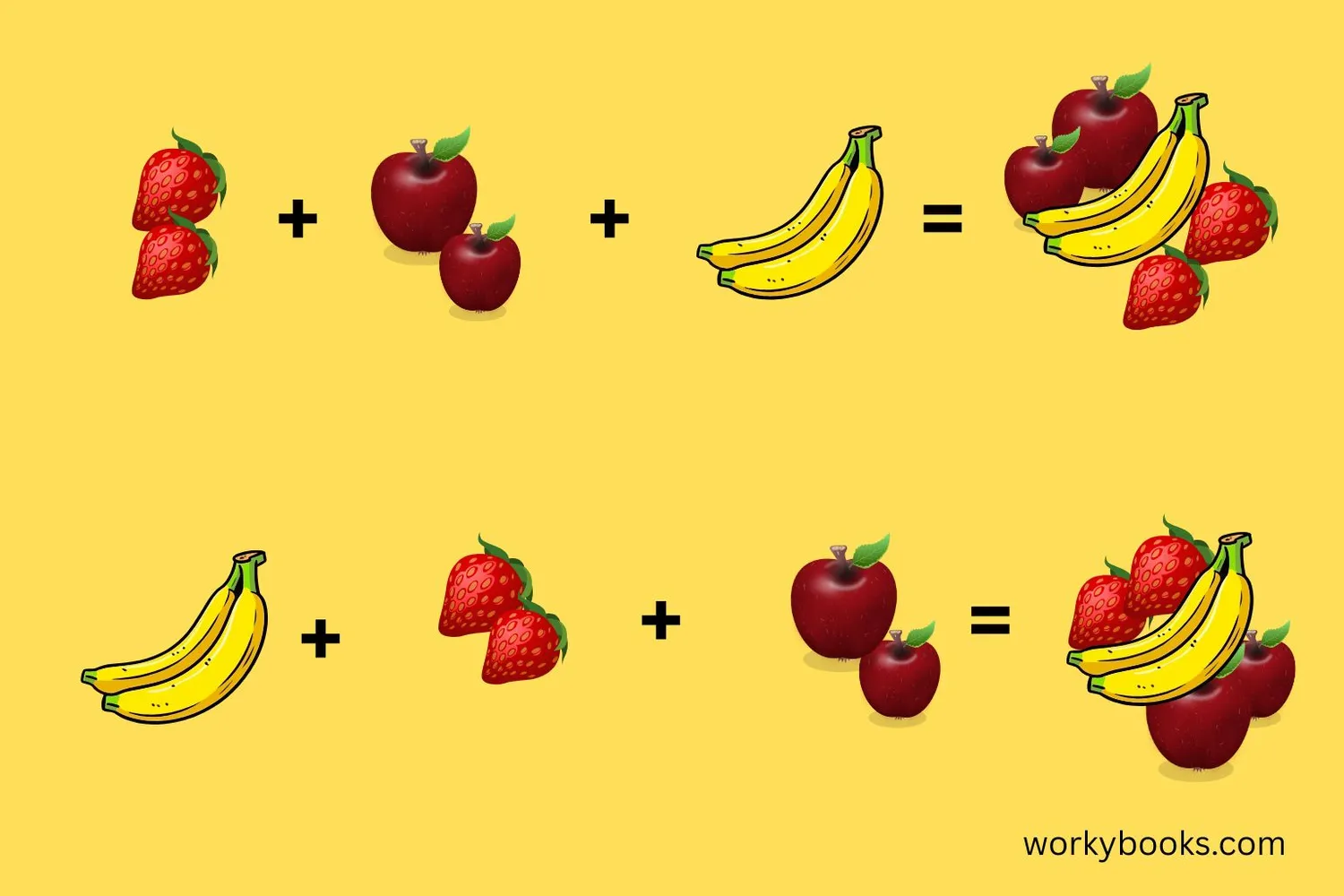
For addition, the associative property means that when we add three or more numbers, it doesn't matter how we group them. The sum will be the same regardless of where we put the parentheses.
Here's an example:
5 + 4 = 2 + 7
9 = 9
Practice Problem
Use the associative property to solve: (7 + 8) + 2
Solution: We can regroup as 7 + (8 + 2) = 7 + 10 = 17
Associative Property of Multiplication
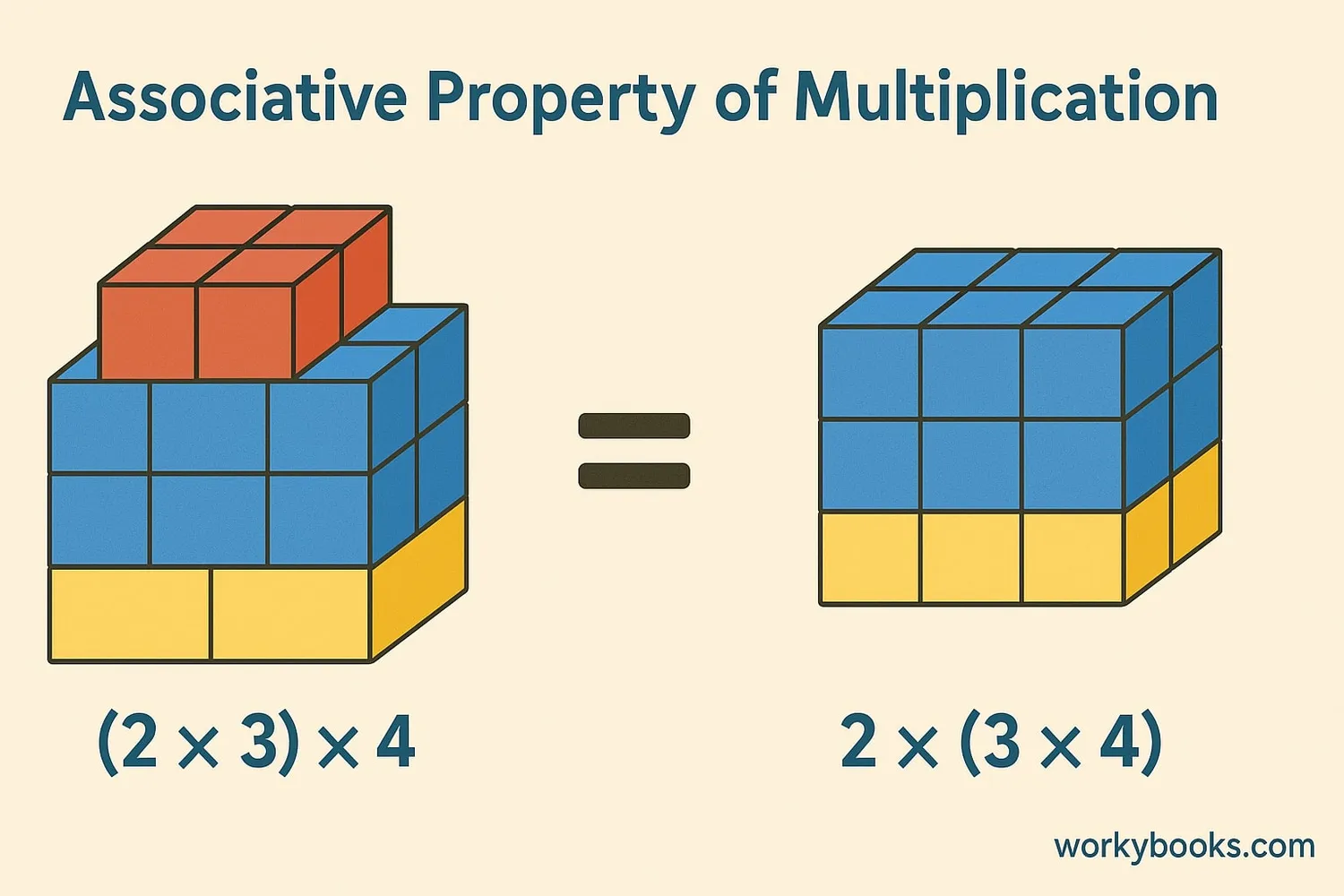
For multiplication, the associative property tells us that we can change the grouping of factors without changing the product. Just like with addition, the parentheses can move without affecting the result.
Here's an example:
6 × 4 = 2 × 12
24 = 24
Practice Problem
Use the associative property to solve: (5 × 3) × 2
Solution: We can regroup as 5 × (3 × 2) = 5 × 6 = 30
Subtraction & Division Exceptions

The associative property does NOT work for subtraction or division. Changing the grouping in subtraction or division problems will usually give you a different result.
Let's see why:
8 - (3 - 2) = 8 - 1 = 7
3 ≠ 7
12 ÷ (3 ÷ 2) = 12 ÷ 1.5 = 8
2 ≠ 8
Remember
Associative property only applies to addition and multiplication. For subtraction and division, the grouping matters!
| Operation | Associative Property Applies? | Example |
|---|---|---|
| Addition | Yes | (a + b) + c = a + (b + c) |
| Multiplication | Yes | (a × b) × c = a × (b × c) |
| Subtraction | No | (a - b) - c ≠ a - (b - c) |
| Division | No | (a ÷ b) ÷ c ≠ a ÷ (b ÷ c) |
Real-World Examples

Let's see how the associative property works in real life:
Example 1: Adding Money
You have $5 in your piggy bank. You earn $3 from chores and $2 from a gift. Does the order matter?
($5 + $3) + $2 = $8 + $2 = $10
$5 + ($3 + $2) = $5 + $5 = $10
Same result!
Example 2: Multiplying Dimensions
A box is 2 feet long, 3 feet wide, and 4 feet high. What's its volume?
(2 × 3) × 4 = 6 × 4 = 24 cubic feet
2 × (3 × 4) = 2 × 12 = 24 cubic feet
Same volume!
Example 3: Combining Ingredients
A recipe needs 2 cups of flour, 1 cup of sugar, and 3 cups of milk. The total liquid and dry ingredients can be grouped differently but the total remains the same.
Math Tip
Use the associative property to make calculations easier. Group numbers that add to 10 or multiply to make round numbers.
Associative Property Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the associative property:
Math Trivia
Discover interesting facts about mathematical properties:
Origin of Properties
The formal study of mathematical properties like associative and commutative began in the 19th century with mathematicians like William Rowan Hamilton and Hermann Grassmann.
Beyond Numbers
The associative property applies to other mathematical concepts too! Matrix multiplication and function composition are associative, but not commutative.
Computer Science
In computer programming, understanding associative properties helps optimize calculations. Compilers rearrange operations to make programs run faster while maintaining correctness.
Memory Advantage
Using the associative property can help with mental math! By grouping numbers that make tens or easy multiples, you can solve problems faster in your head.





