Closure Property in Mathematics - Definition, Examples, Quiz, FAQ, Trivia
Learn how numbers stay within sets when we add, subtract, multiply, or divide them
What is the Closure Property?

The Closure Property is a fundamental concept in mathematics. It tells us that when we perform an operation (like addition, subtraction, multiplication, or division) on numbers from a particular set, the result will also belong to the same set.
Think of it like a club with specific membership rules. If you combine two members using the club's rules, you get another member of the same club. For example:
- When we add two whole numbers (like 3 + 4 = 7), we get another whole number. So whole numbers are closed under addition.
- But when we divide two whole numbers (like 3 ÷ 4 = 0.75), we don't always get a whole number. So whole numbers are not closed under division.
Key Concept
A set of numbers is closed under an operation if performing that operation on any two numbers in the set always produces another number in the same set.
Closure Property for Different Operations

The Closure Property works differently for each mathematical operation. Let's explore how it applies to the four basic operations:
Addition: Most number sets are closed under addition. For example:
- Natural numbers: 4 + 5 = 9 (natural number)
- Integers: -3 + 7 = 4 (integer)
Subtraction: Some number sets are closed under subtraction, others are not:
- Integers: 5 - 8 = -3 (integer, closed)
- Natural numbers: 5 - 8 = -3 (not natural, not closed)
Multiplication: Similar to addition, most sets are closed under multiplication:
- Rational numbers: 1/2 × 2/3 = 1/3 (rational)
- Whole numbers: 3 × 0 = 0 (whole number)
Division: Division is special because most sets are not closed under division:
- Integers: 5 ÷ 2 = 2.5 (not integer, not closed)
- Rational numbers: 4/5 ÷ 2/3 = 6/5 (rational, closed)
Remember
Division by zero is undefined! Even if a set is closed under division, we can't divide by zero.
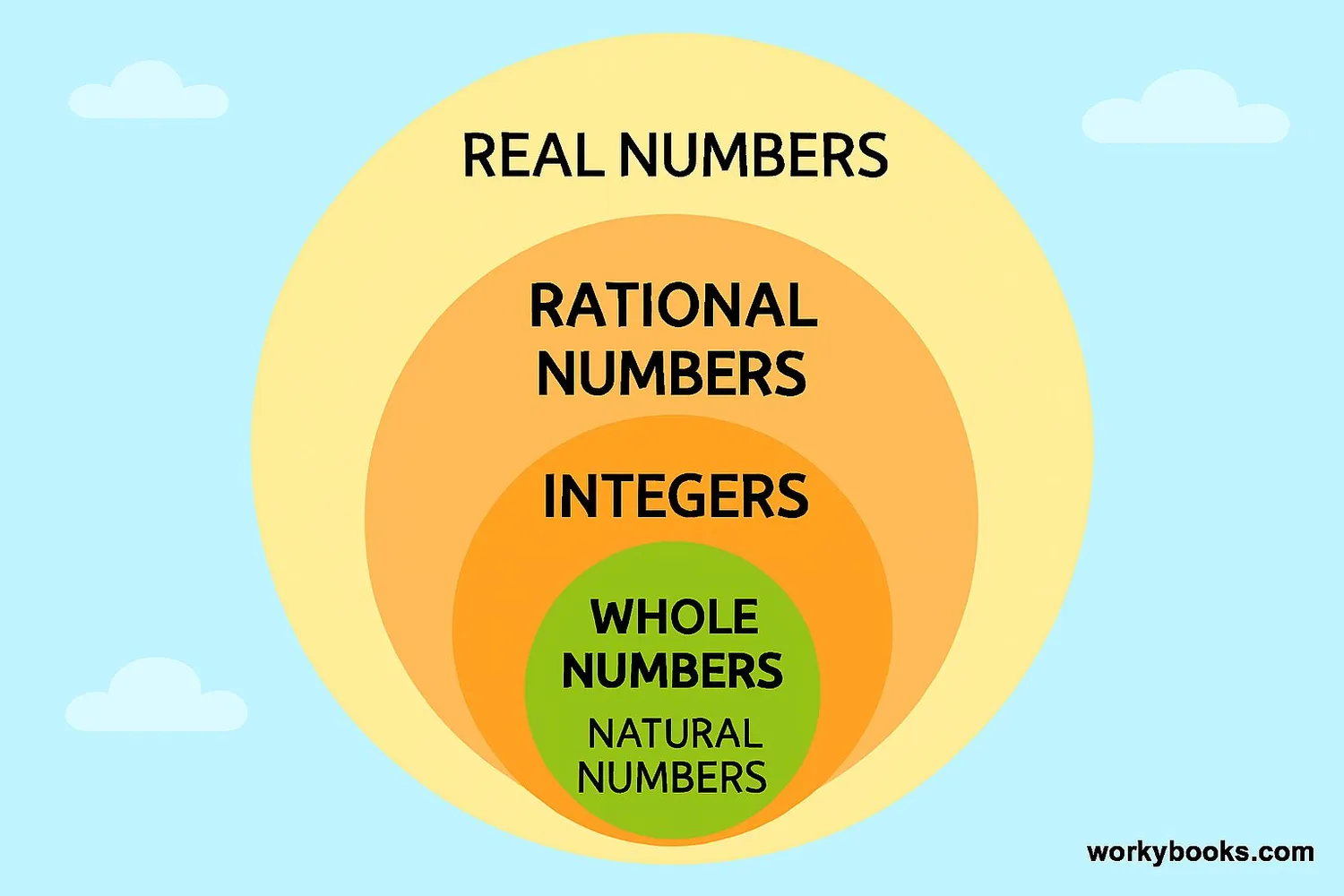
Closure Property for Different Number Sets

Different sets of numbers have different closure properties. Let's examine some common number sets:
Natural Numbers
{1, 2, 3, 4, ...}
Closed under: Addition and Multiplication
Not closed under: Subtraction and Division
Whole Numbers
{0, 1, 2, 3, 4, ...}
Closed under: Addition and Multiplication
Not closed under: Subtraction and Division
Integers
{..., -3, -2, -1, 0, 1, 2, 3, ...}
Closed under: Addition, Subtraction, Multiplication
Not closed under: Division
Rational Numbers
Fractions: a/b where b ≠ 0
Closed under: All four operations (except division by zero)
Closure Property Summary
| Number Set | Addition | Subtraction | Multiplication | Division |
|---|---|---|---|---|
| Natural Numbers | Yes | No | Yes | No |
| Whole Numbers | Yes | No | Yes | No |
| Integers | Yes | Yes | Yes | No |
| Rational Numbers | Yes | Yes | Yes | Yes* |
| Real Numbers | Yes | Yes | Yes | Yes* |
*Except division by zero
Pattern to Notice
The larger the number set, the more operations it's closed under. Rational and real numbers are closed under all four basic operations (except division by zero).
Real-World Examples
The Closure Property appears in many real-world situations. Let's look at some examples:
Example 1: Scorekeeping
In a basketball game, points are always whole numbers (2, 3, or 1). When you add points from different plays:
2 + 3 + 2 = 7 (still a whole number)
This shows that whole numbers are closed under addition for scoring.
Example 2: Temperature Changes
Temperatures can be positive or negative (integers). The difference between temperatures:
5°C - (-3°C) = 8°C (still an integer)
This shows integers are closed under subtraction.
Example 3: Recipe Measurements
When baking, you might need to halve a recipe:
1/2 cup flour × 1/2 = 1/4 cup flour (still a rational number)
This shows rational numbers are closed under multiplication.
Example 4: Science Measurements
When measuring lengths in science, you might add different measurements:
3.2 cm + 1.7 cm = 4.9 cm (still a real number)
This shows real numbers are closed under addition.
Application Tip
Whenever you work with numbers in the real world, think about what number set you're using and whether your operations will keep results in that set.
Closure Property Practice Quiz
Test your understanding of the closure property with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the closure property:
Math Trivia
Discover interesting facts about numbers and the closure property:
Historical Development
The concept of closure was first formally developed in the 19th century by mathematicians working on abstract algebra. They needed to understand which operations preserved the structure of different number systems.
Beyond Numbers
The closure property applies to more than just numbers. Sets of shapes can be closed under operations like rotation. For example, rotating a square by 90° gives another square, so squares are closed under 90° rotations.
Infinite Sets
All the number sets we've discussed (natural, whole, integers, rational, real) are infinite sets. The closure property helps mathematicians work with these infinite sets systematically.
Computer Science
In computer science, closure is an important concept in programming. When a function "closes over" its environment, it can remember variables from its creation context, even when called elsewhere.





