Cone - Definition, Examples, Quiz, FAQ, Trivia
Learn about cones: their parts, types, volume, surface area, and real-world examples
What is a Cone?

A cone is a three-dimensional geometric shape that tapers smoothly from a flat circular base to a point called the apex or vertex. Think of an ice cream cone or a party hat!
Cones are all around us in everyday life: traffic cones, ice cream cones, and even volcanoes have a cone shape. In mathematics, cones are important shapes that help us understand volume and surface area concepts.
Cones are similar to pyramids, but while pyramids have polygonal bases, cones have circular bases. This circular base makes cones special and gives them unique mathematical properties.
Key Concept
A cone has one circular base and one apex. The distance from the base to the apex is the height of the cone.
Parts of a Cone
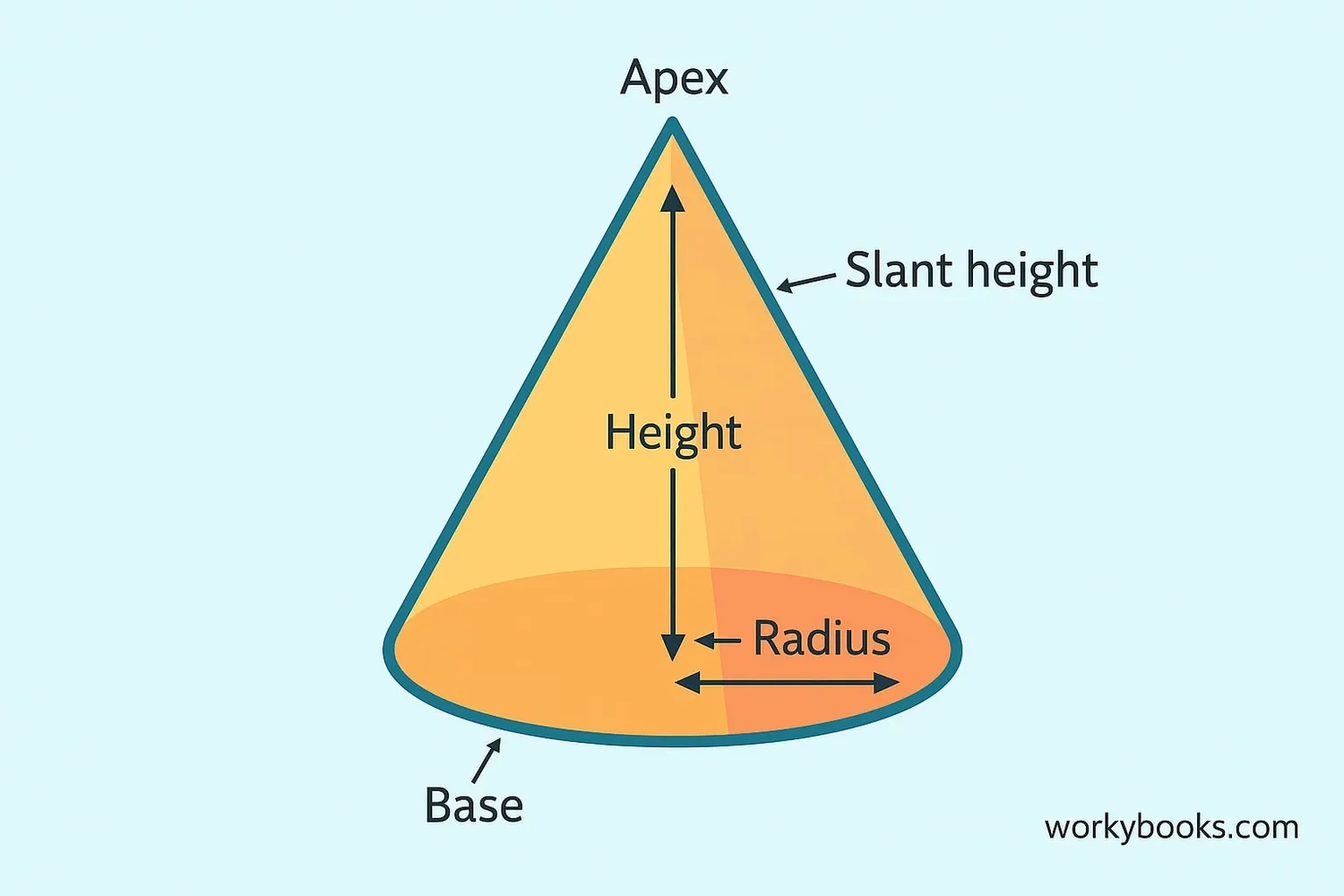
Let's learn about the different parts of a cone:
Apex (Vertex)
The pointed tip of the cone where all the sides meet.
Base
The flat circular surface at the bottom of the cone.
Height (h)
The perpendicular distance from the base to the apex.
Radius (r)
The distance from the center of the base to its edge.
Slant Height (l)
The distance from the apex to any point on the edge of the base.
The slant height is always longer than the actual height because it's measured along the side of the cone. These parts are important when we calculate the volume and surface area of a cone.
Remember
The radius and height form a right triangle with the slant height: l = √(r² + h²)
Types of Cones
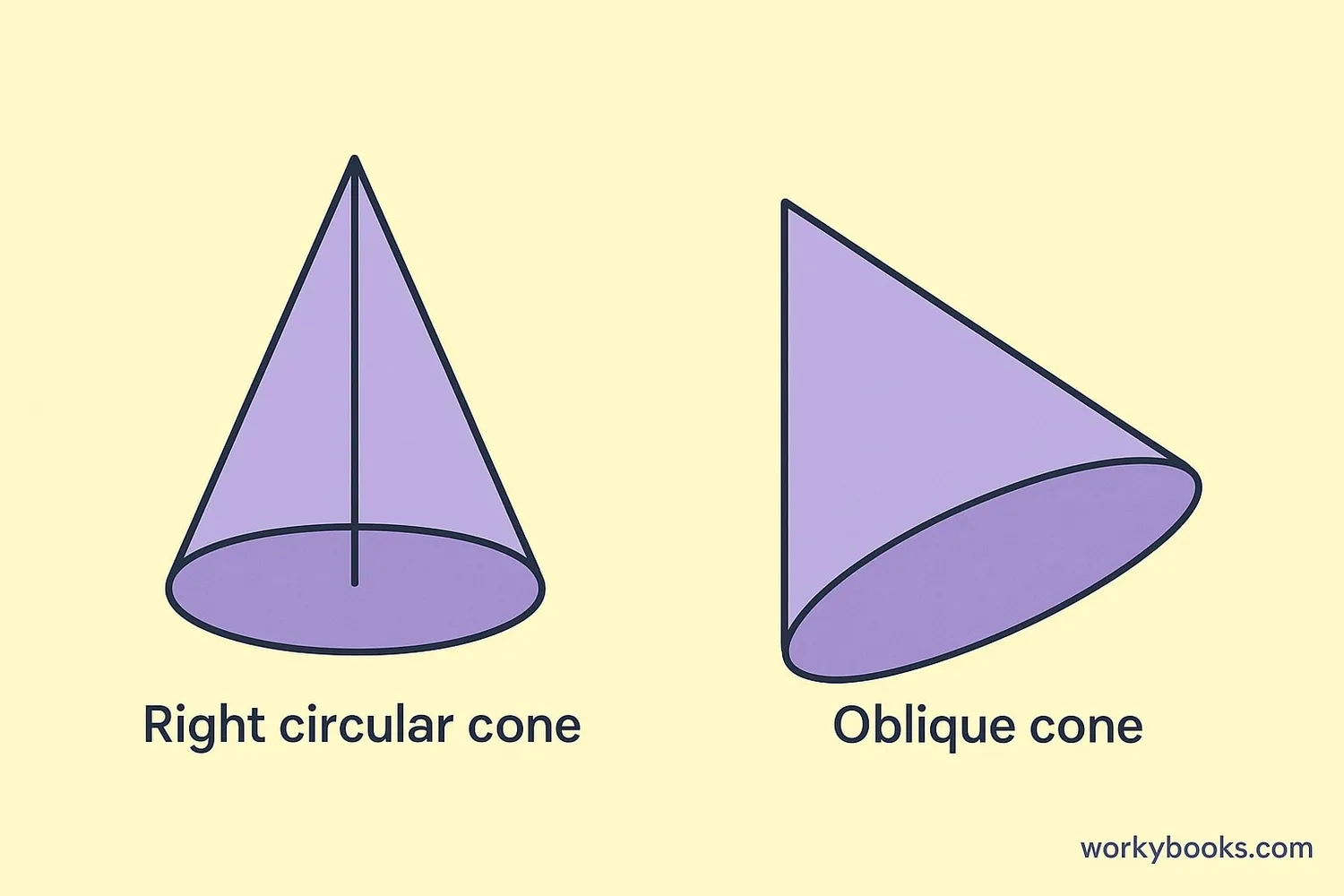
There are two main types of cones in geometry:
Right Circular Cone
This is the most common type of cone. The apex is directly above the center of the base, forming a right angle with the base. Most mathematical formulas are for right circular cones.
Oblique Cone
In this type, the apex is not directly above the center of the base. The cone appears to be leaning to one side. These are less common in mathematics but appear in some real-world objects.
Real-world Examples

Ice cream cone

Traffic cone

party hat

Volcano
Volume of a Cone
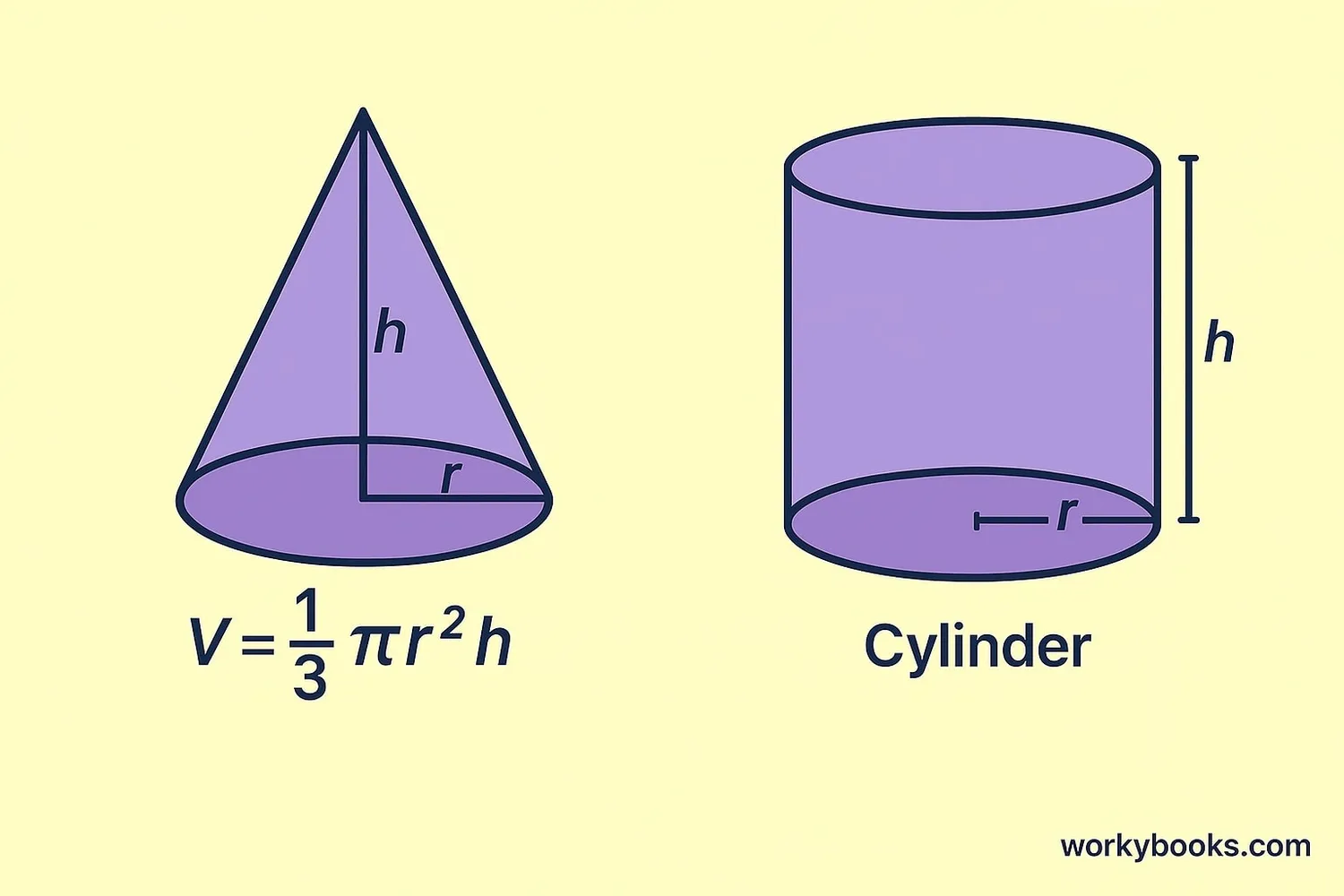
The volume of a cone tells us how much space is inside it. The formula is:
Volume Formula
Where V is volume, r is the radius of the base, and h is the height of the cone.
Why one-third? Because a cone is exactly one-third the volume of a cylinder with the same base and height! Try filling a cone with water and pouring it into a cylinder with the same base and height - it will take exactly three cones to fill the cylinder.
Example: Find the volume of a cone with radius 3 cm and height 7 cm.
Step 1: Write the formula → V = (1/3)πr²h
Step 2: Plug in values → V = (1/3)π(3)²(7)
Step 3: Calculate → V = (1/3)π(9)(7) = (1/3)π(63) = 21π ≈ 65.97 cm³
Volume Tip
Remember that volume is always measured in cubic units (cm³, m³, etc.) because it measures three-dimensional space.
Surface Area of a Cone

The surface area of a cone is the total area of its outer surfaces. A cone has two parts:
1. Base Area: The area of the circular base → A_base = πr²
2. Lateral Surface Area: The area of the side surface → A_lateral = πrl
So the total surface area is:
Surface Area Formula
Where r is the radius, and l is the slant height.
Example: Find the surface area of a cone with radius 4 cm and slant height 8 cm.
Step 1: Calculate base area → π(4)² = 16π cm²
Step 2: Calculate lateral surface area → π(4)(8) = 32π cm²
Step 3: Add them together → 16π + 32π = 48π ≈ 150.8 cm²
Surface Area Tip
If you don't have the slant height, remember that l = √(r² + h²) using the Pythagorean theorem.
Frustum of a Cone
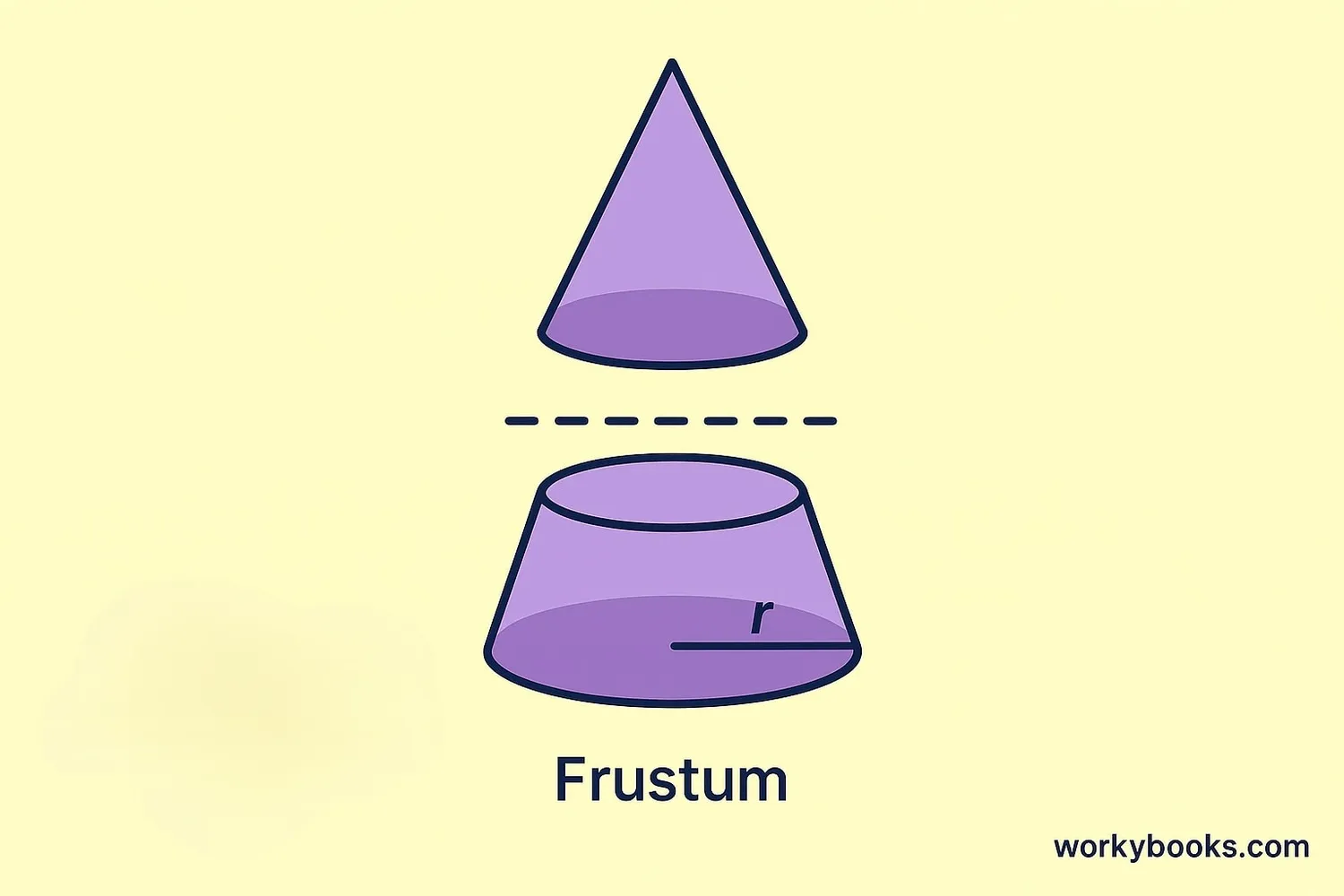
A frustum is what you get when you slice off the top of a cone with a cut parallel to the base. It looks like a cone with its pointed top removed.
Frustums are common in everyday objects like buckets, lampshades, and certain types of drinking cups. They have two circular bases - a larger one at the bottom and a smaller one at the top.
The volume of a frustum can be calculated using the formula:
V = (1/3)πh(R² + Rr + r²)
Where h is the height of the frustum, R is the radius of the larger base, and r is the radius of the smaller base.
Frustum Example
A typical bucket is a frustum. Its wider bottom provides stability, while the narrower top makes it easier to carry.
Cone Knowledge Quiz
Test what you've learned with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about cones:
Cone Trivia
Discover interesting facts about cones:
Ancient Mathematics
The Greek mathematician Archimedes discovered the relationship between the volumes of cones, spheres, and cylinders over 2,200 years ago!
Pine Cones
Pine cones have a spiral pattern that follows the Fibonacci sequence. This helps the seeds pack efficiently as the cone opens and closes with humidity changes.
Space Capsules
Early space capsules like the Apollo command module used a cone shape because it provides stability during re-entry into Earth's atmosphere.
Sound Cones
Many speakers use cone-shaped diaphragms because this shape efficiently moves air to produce sound waves with minimal distortion.





