Congruent Shapes - Definition, Examples, Quiz, FAQ, Trivia
Learn about congruence in geometry with simple explanations and practice activities
What is Congruence?
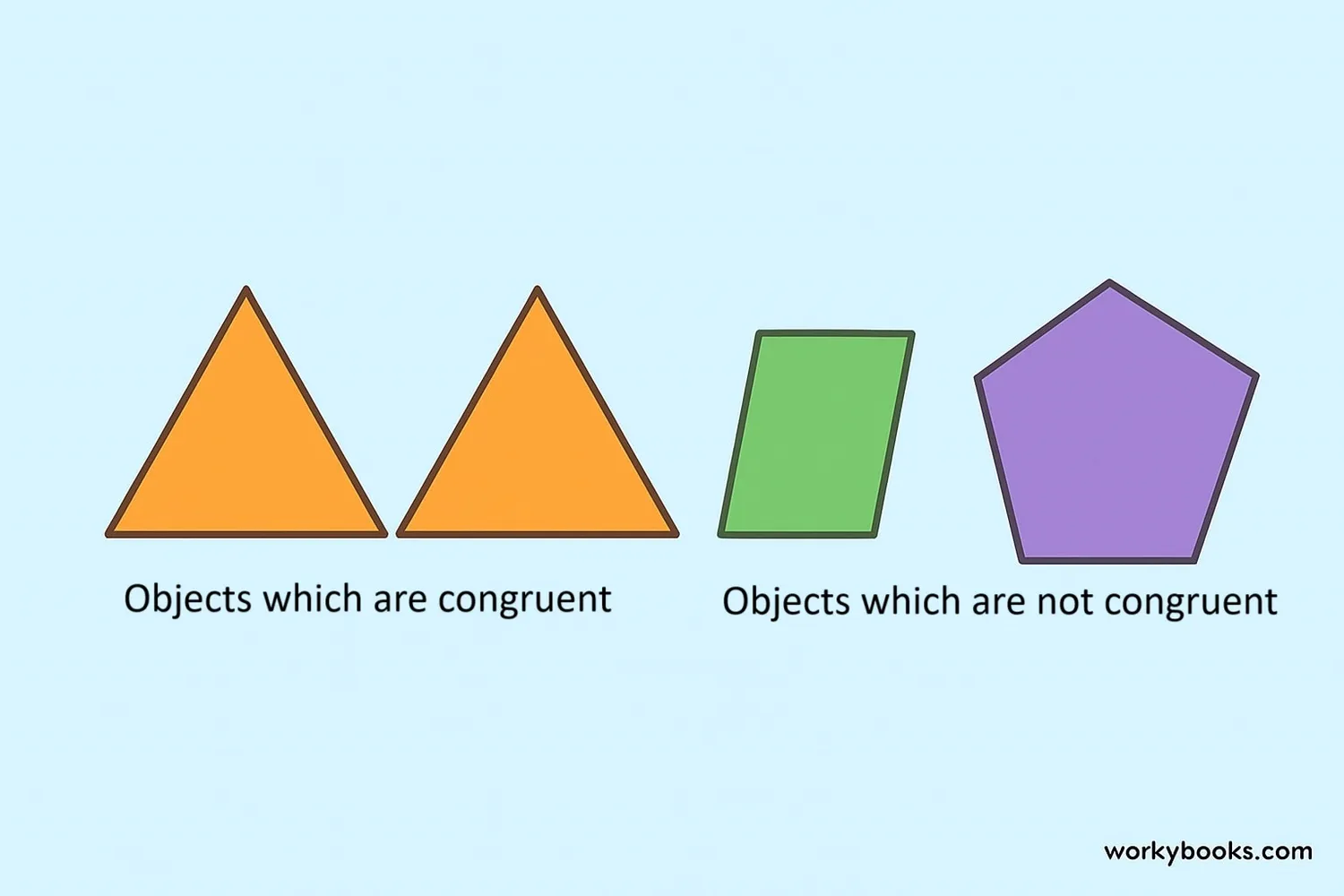
In geometry, two shapes are congruent if they have exactly the same size and shape. This means that if you could pick one shape up and place it exactly on top of the other, they would match perfectly.
The word "congruent" comes from the Latin word "congruere" which means "to come together" or "to agree."
Key properties of congruent shapes:
- All corresponding sides are equal in length
- All corresponding angles are equal in measure
- They have the same area and perimeter
Key Concept
Congruent shapes are identical in every way - they're perfect copies of each other!
Congruent vs Similar Figures
It's important to understand the difference between congruent and similar shapes:
Same size, same shape
Same shape, different size
- Have exactly the same size and shape
- All corresponding sides and angles are equal
- The symbol for congruence is ≅
- Have the same shape but different sizes
- Corresponding angles are equal, but sides are proportional
- The symbol for similarity is ∼
Congruence Theorems for Triangles
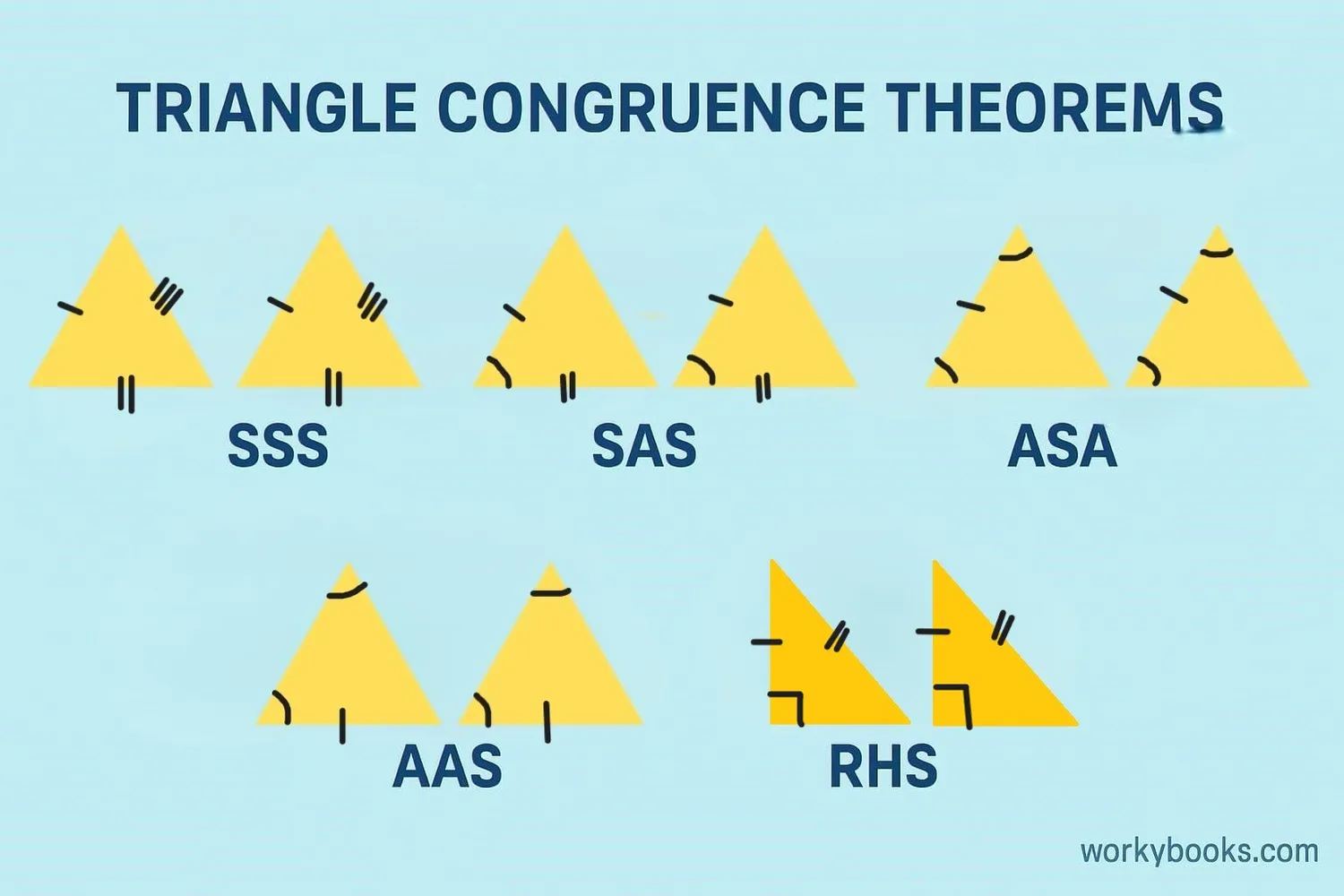
For triangles, we have special rules called congruence theorems that help us prove if two triangles are congruent. Here are the five main theorems:
SSS Side-Side-Side
If all three sides of one triangle are equal to all three sides of another triangle, the triangles are congruent.
SAS Side-Angle-Side
If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, the triangles are congruent.
ASA Angle-Side-Angle
If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, the triangles are congruent.
AAS Angle-Angle-Side
If two angles and a non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, the triangles are congruent.
RHS Right-Hypotenuse-Side
If the hypotenuse and one side of a right-angled triangle are equal to the hypotenuse and one side of another right-angled triangle, the triangles are congruent.
Remember
These theorems only work for triangles! For other shapes, we need to check all sides and angles to prove congruence.
Real-World Examples

Congruence isn't just a math concept - we see it all around us! Here are some real-world examples:
Example 1: Building Blocks
Identical Lego blocks are congruent because they have the same size and shape. You can stack them perfectly.
Example 2: Cookies
Cookies made with the same cookie cutter are congruent. They match perfectly when placed on top of each other.
Example 3: Puzzle Pieces
Identical puzzle pieces are congruent shapes. Each piece fits exactly where it belongs.
Example 4: Windows in a Building
In many buildings, windows of the same size and shape are congruent to each other.
Example 5: Wheels on a Car
All four wheels on a car are congruent circles (if they're the same size!).
Try This
Look around your classroom or home. Can you find any pairs of congruent objects?
Congruence Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about congruence:
Geometry Trivia
Discover interesting facts about congruence and geometry:
Ancient Use of Congruence
Ancient Egyptians used congruence concepts when building pyramids. They ensured that stones were cut to identical sizes and shapes so they would fit together perfectly.
Congruence in Nature
Honeybees build honeycombs with congruent hexagonal cells. This efficient shape allows them to store the most honey using the least amount of wax.
Congruence in Math History
The concept of congruence dates back to Euclid (300 BC) in his book "Elements." He established the foundations of geometry that we still use today.
Art and Congruence
Artists use congruence in patterns like tessellations. M.C. Escher's famous artworks use congruent shapes that fit together perfectly with no gaps.


