Cuboid - Definition, Examples, Quiz, FAQ, Trivia
Learn about cuboids with easy explanations, properties, formulas, examples, and quizzes
What is a Cuboid?
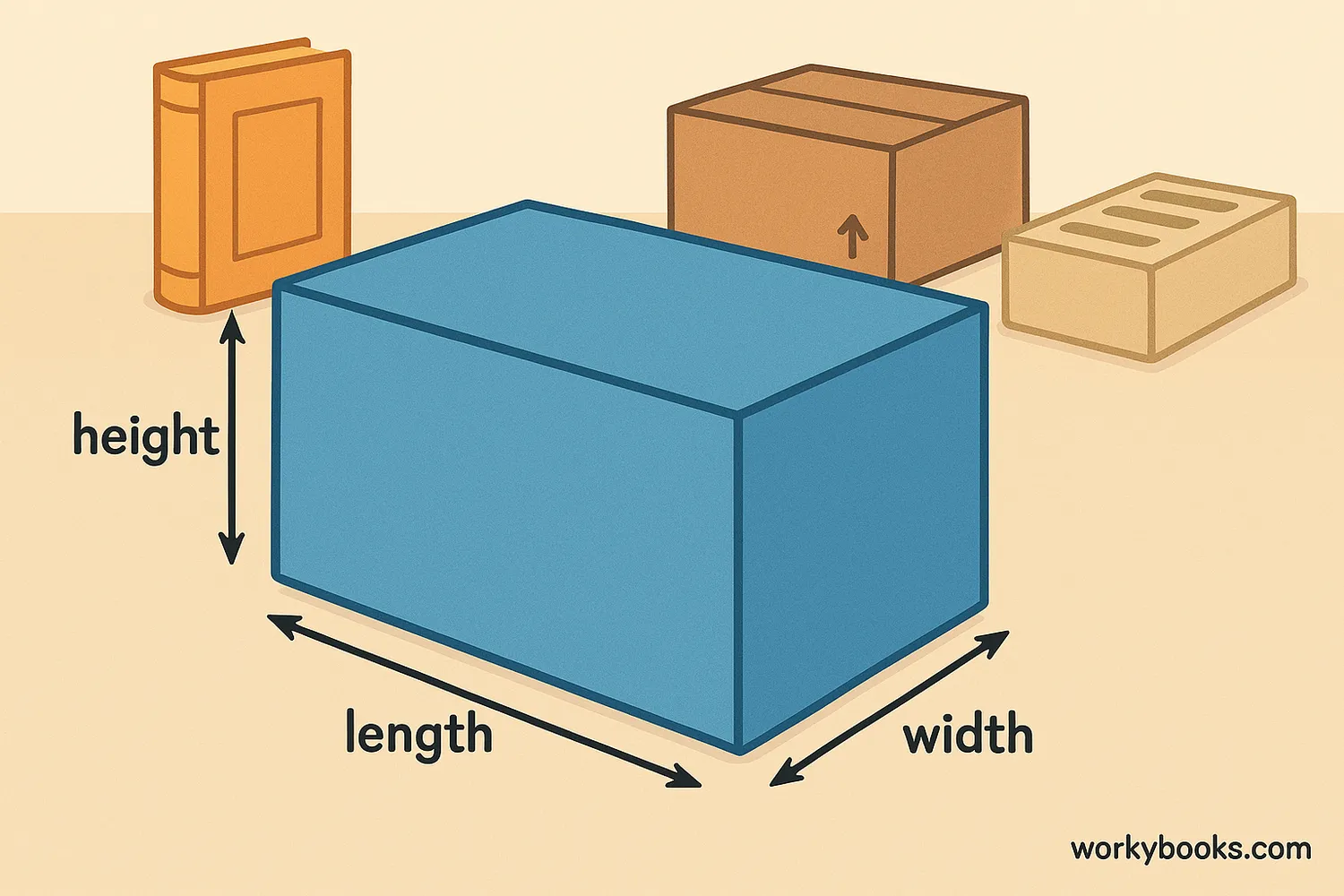
A cuboid is a 3-dimensional shape with six rectangular faces. All its angles are right angles (90 degrees), and opposite faces are equal. You might also hear it called a rectangular prism.
Think of a cuboid as a stretched cube. While a cube has all sides equal, a cuboid has three pairs of equal sides: length, width, and height. Many everyday objects are cuboids - like books, boxes, and bricks!
Key characteristics:
- 6 rectangular faces
- 12 straight edges
- 8 vertices (corners)
- All angles are right angles (90°)
- Opposite faces are identical
Key Concept
A cuboid is a 3D shape with six rectangular faces, where opposite faces are identical and all angles are right angles.
Properties of a Cuboid
Let's explore the key properties of cuboids:
Faces: A cuboid has 6 faces. Each face is a rectangle. Opposite faces are identical.
Edges: A cuboid has 12 edges. Each edge is a straight line where two faces meet.
Vertices: A cuboid has 8 vertices (corners). At each vertex, three edges meet.
Dimensions: Every cuboid has three dimensions:
- Length (l) - the longest side
- Width (w) - the shorter side on the base
- Height (h) - how tall the cuboid is
The space diagonal of a cuboid connects opposite corners through the interior. Its length can be found using: √(l² + w² + h²)
Remember
All cuboids are rectangular prisms, but not all rectangular prisms are cubes. A cube is a special type of cuboid where all sides are equal.
Volume of a Cuboid
The volume of a cuboid tells us how much space it takes up. To find the volume, we multiply its three dimensions together:
Volume Formula
Where V = volume, l = length, w = width, h = height
Example: Find the volume of a cuboid with length 5cm, width 3cm, and height 2cm.
Step 1: Identify the dimensions → l = 5cm, w = 3cm, h = 2cm
Step 2: Apply the formula → V = 5 × 3 × 2
Step 3: Calculate → 30 cm³ (cubic centimeters)
So this cuboid has a volume of 30 cubic centimeters. That means it would take 30 cubes, each 1cm × 1cm × 1cm, to fill it completely!
Volume Tip
Volume is always measured in cubic units. For example: cubic centimeters (cm³), cubic meters (m³), or cubic feet (ft³).
Surface Area of a Cuboid
The surface area of a cuboid is the total area of all its faces. Since a cuboid has three pairs of identical faces, we can calculate surface area with:
Surface Area Formula
Where SA = surface area, l = length, w = width, h = height
Example: Find the surface area of a cuboid with length 6cm, width 4cm, and height 3cm.
Step 1: Calculate each face area:
- Front/back: 6 × 3 = 18cm² each
- Top/bottom: 6 × 4 = 24cm² each
- Sides: 4 × 3 = 12cm² each
Or using the formula: 2((6×4) + (6×3) + (4×3)) = 2(24 + 18 + 12) = 2×54 = 108cm²
So this cuboid has a surface area of 108 square centimeters. That's how much wrapping paper you'd need to cover it completely!
Remember
Surface area is measured in square units (like cm² or m²) because it's covering a surface.
Real-World Cuboid Examples

Cuboids are all around us! Here are some common examples:
Books: Most books are perfect cuboids with length, width, and thickness.
Bricks: Building bricks are classic cuboids that stack easily.
Shipping Boxes: Cardboard boxes are cuboids designed to hold and protect items.
Refrigerators: These appliances are large cuboids that keep food cold.
Building Blocks: Many children's building toys use cuboid shapes.
Matchboxes: Small containers that hold matches are typically cuboids.
Can you find cuboids in your classroom? Look for objects with six rectangular faces and right-angle corners!
Did You Know?
The Great Pyramid of Giza was originally shaped like a cuboid before erosion and stone removal changed its appearance!
Cuboid Quiz
Test your knowledge about cuboids with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about cuboids:
Cuboid Trivia
Discover interesting facts about cuboids and geometry:
Ancient Architecture
The ancient Egyptians used cuboid-shaped stones to build the pyramids. Each stone was carefully shaped to fit perfectly with its neighbors.
Crystal Structures
Many minerals form natural cuboid crystals. The mineral galena (lead ore) often forms perfect cube-shaped crystals that look like small cuboids.
Space Modules
The International Space Station contains many cuboid-shaped modules. These rectangular shapes make efficient use of space inside rockets during launch.
Largest Cuboid Building
The world's largest cuboid-shaped building is the Merchandise Mart in Chicago. It covers 4.2 million square feet - that's about 78 football fields!





