Difference Quotient - Definition, Examples, Quiz, FAQ, Trivia
Learn about slopes, rates of change, and how they connect to calculus
What is the Difference Quotient?
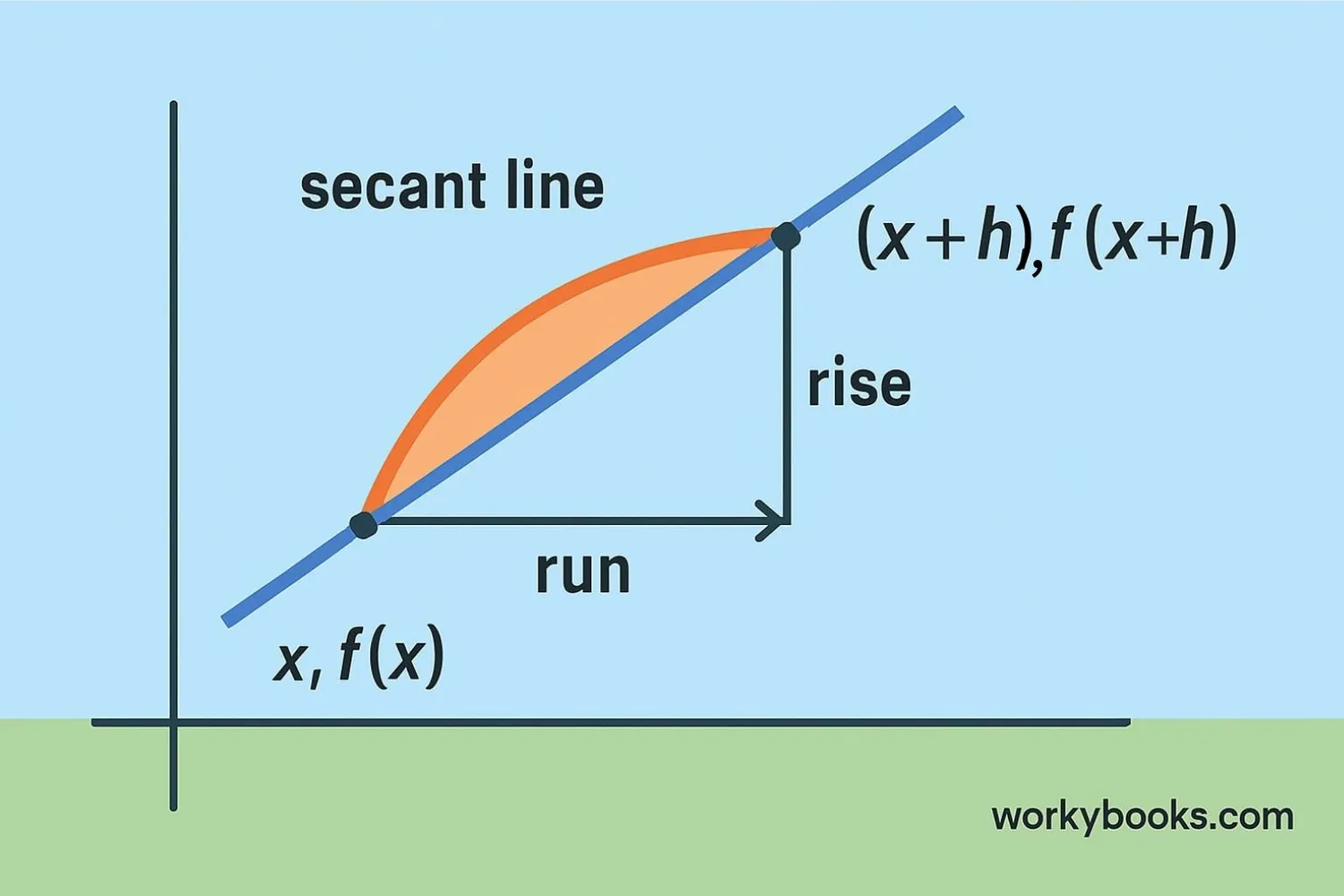
The difference quotient is a special math tool that helps us understand how things change. Imagine you're on a hike - the difference quotient tells you how steep the trail is between two points. In math terms, it measures the average rate of change of a function over an interval.
Think of it like this: If you have a graph of how much water is in a bathtub over time, the difference quotient tells you how fast the water level is changing between two moments. It's like calculating the slope of a straight line connecting two points on a curve.
The difference quotient is important because it's the first step toward understanding derivatives in calculus, which tell us about instantaneous rates of change.
Key Concept
The difference quotient is a "slope calculator" for curves. It measures how steep a curve is between two points.
Why Does the Difference Quotient Matter?
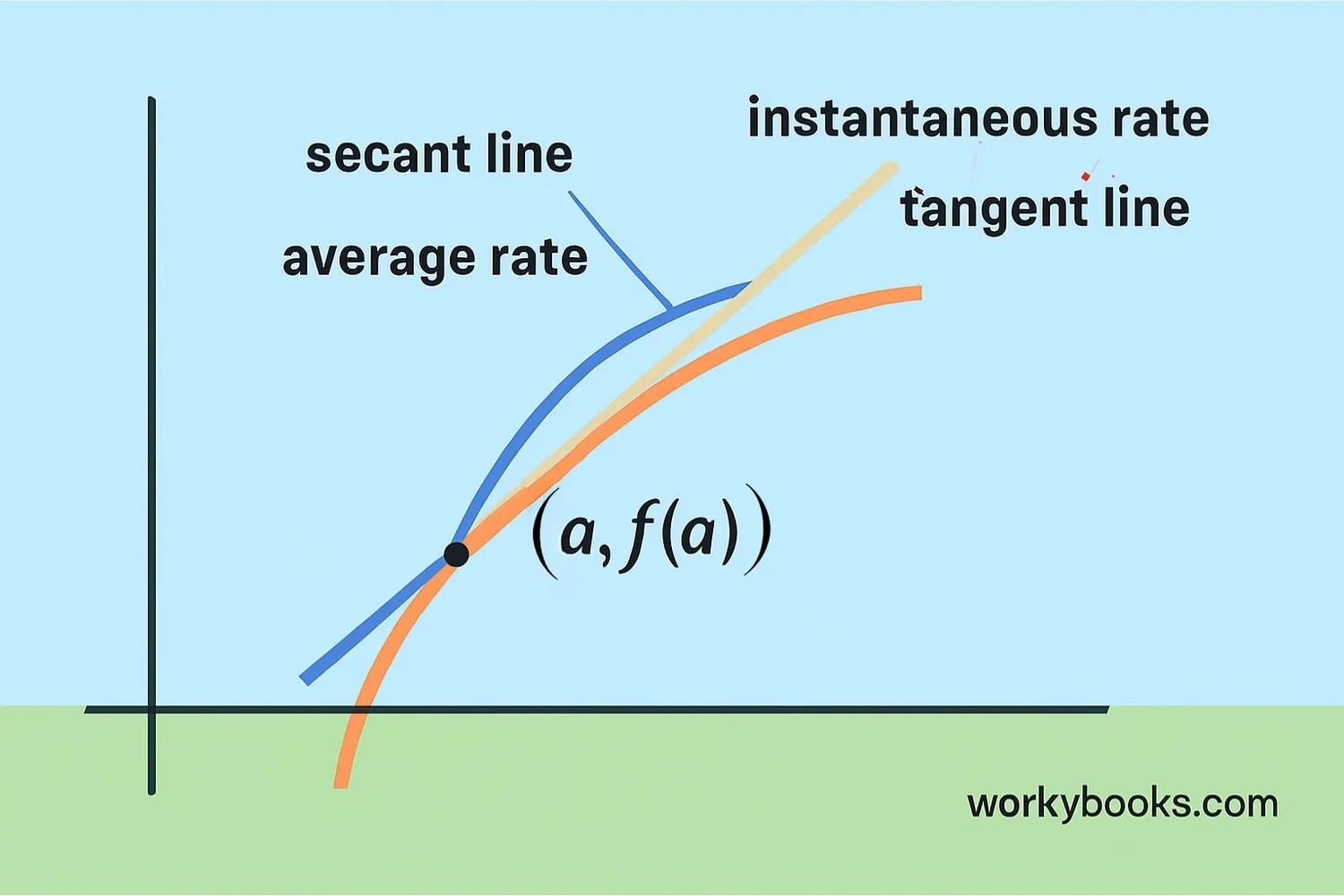
The difference quotient is super important because:
1. It's the foundation of calculus: The difference quotient is how we define derivatives. When we make the interval between points smaller and smaller (using limits), we get the derivative - which tells us the exact slope at a single point.
2. It measures real-world changes: Whether it's how fast a car is accelerating, how quickly a population is growing, or how steep a hill is, the difference quotient helps us calculate these rates of change.
3. It connects algebra to calculus: The difference quotient shows how algebra concepts (like slope) connect to calculus concepts (like derivatives). It's a bridge between these important areas of math.
Think of the difference quotient as a "zoom lens" for math. When we zoom in super close on a curve, it starts to look straight, and the difference quotient helps us measure that straight-line slope at any point we choose.
Remember
The difference quotient gives the average slope between two points. The derivative gives the exact slope at a single point.
The Difference Quotient Formula
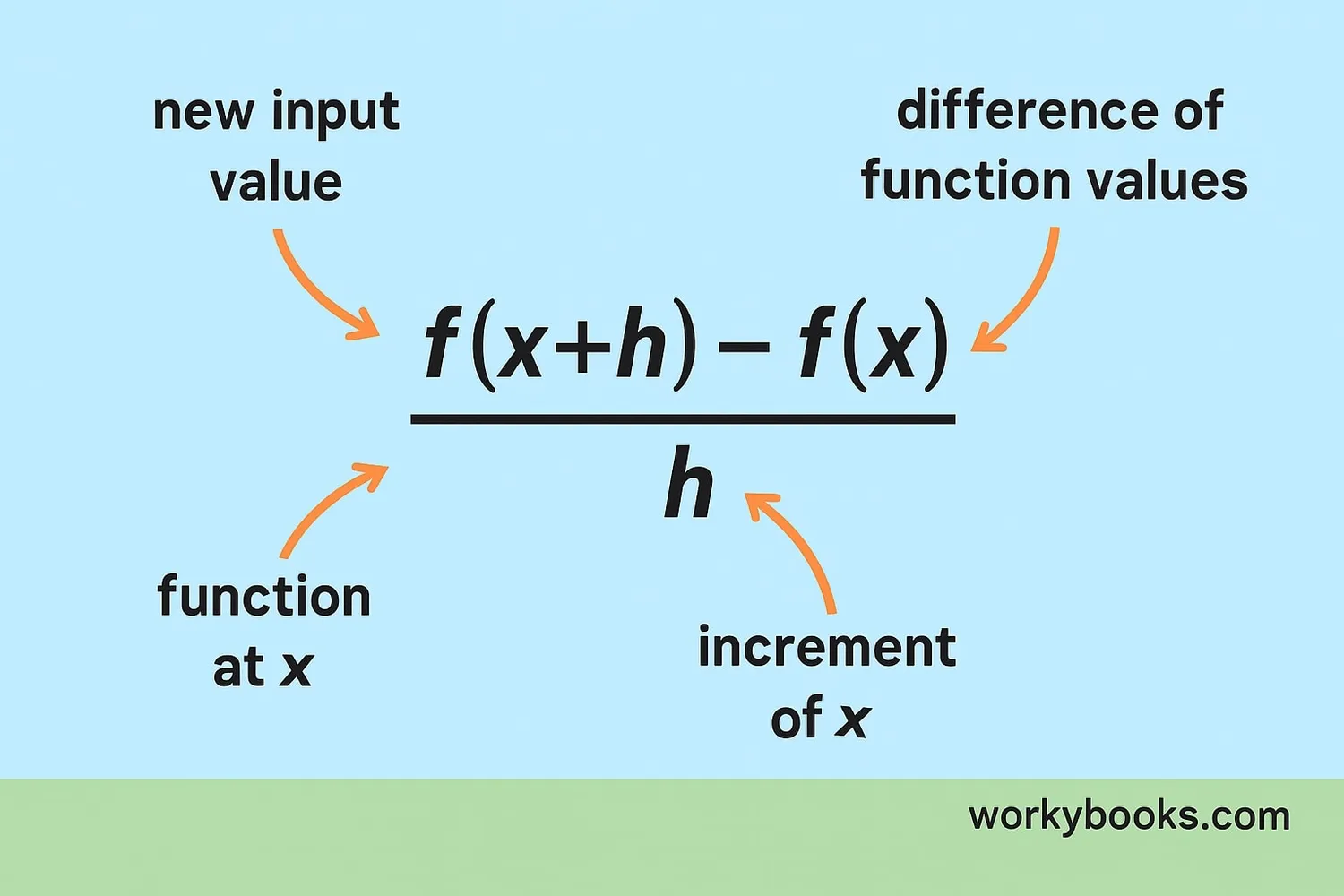
The difference quotient has a special formula that looks like this:
Difference Quotient Formula
This formula calculates the average rate of change of function f between x and x+h.
f(x): The value of the function at point x
f(x+h): The value of the function at a nearby point (x+h)
h: The small distance between the two points
[f(x+h) - f(x)]: The change in function values (rise)
h: The change in x-values (run)
So the whole formula is just rise over run - the same way we calculate slope for straight lines, but now for curves!
Formula Tip
h represents a small change in the x-direction. As h gets closer to zero, the difference quotient becomes the derivative.
Step-by-Step Example

Let's calculate the difference quotient for a simple function: f(x) = x² at x = 2 with h = 1
Step 1: Write the formula
Difference Quotient = [f(x+h) - f(x)] ÷ h
Step 2: Calculate f(x)
Since x = 2 and f(x) = x²:
f(2) = 2² = 4
Step 3: Calculate f(x+h)
Since h = 1, x+h = 2+1 = 3:
f(3) = 3² = 9
Step 4: Plug into the formula
Difference Quotient = [f(3) - f(2)] ÷ 1 = (9 - 4) ÷ 1 = 5
Step 5: Interpret the result
This means the average slope between x=2 and x=3 is 5.
f(2) = 4
Difference Quotient = (4.41 - 4) ÷ 0.1 = 0.41 ÷ 0.1 = 4.1
Notice how with a smaller h (0.1 instead of 1), we got a slope of 4.1, which is closer to the actual slope at x=2 (which is 4).
Practice Tip
Try calculating the difference quotient for different functions and different h values. Notice how the result changes as h gets smaller!
Practice Quiz
Test your understanding of the difference quotient with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about the difference quotient:
Math Trivia
Discover interesting facts about calculus and the difference quotient:
The Birth of Calculus
The concepts behind the difference quotient were developed independently by Isaac Newton and Gottfried Leibniz in the late 17th century. Their work created the entire field of calculus!
Calculus in Nature
Bees solve calculus problems every day! When they fly from flower to flower, they naturally find the most efficient path, solving what mathematicians call the "Traveling Salesman Problem".
Calculus in Space
NASA uses calculus concepts derived from the difference quotient to calculate rocket trajectories. The difference quotient helps them determine exactly when and how to launch rockets to reach other planets!
Calculus Everywhere
Calculus is used in almost every scientific field - from predicting weather patterns and designing bridges to creating computer graphics in movies and video games!





