Differential Equations - Definition, Examples, Quiz, FAQ, Trivia
Learn about equations that describe how things change with easy explanations and examples
What is a Differential Equation?
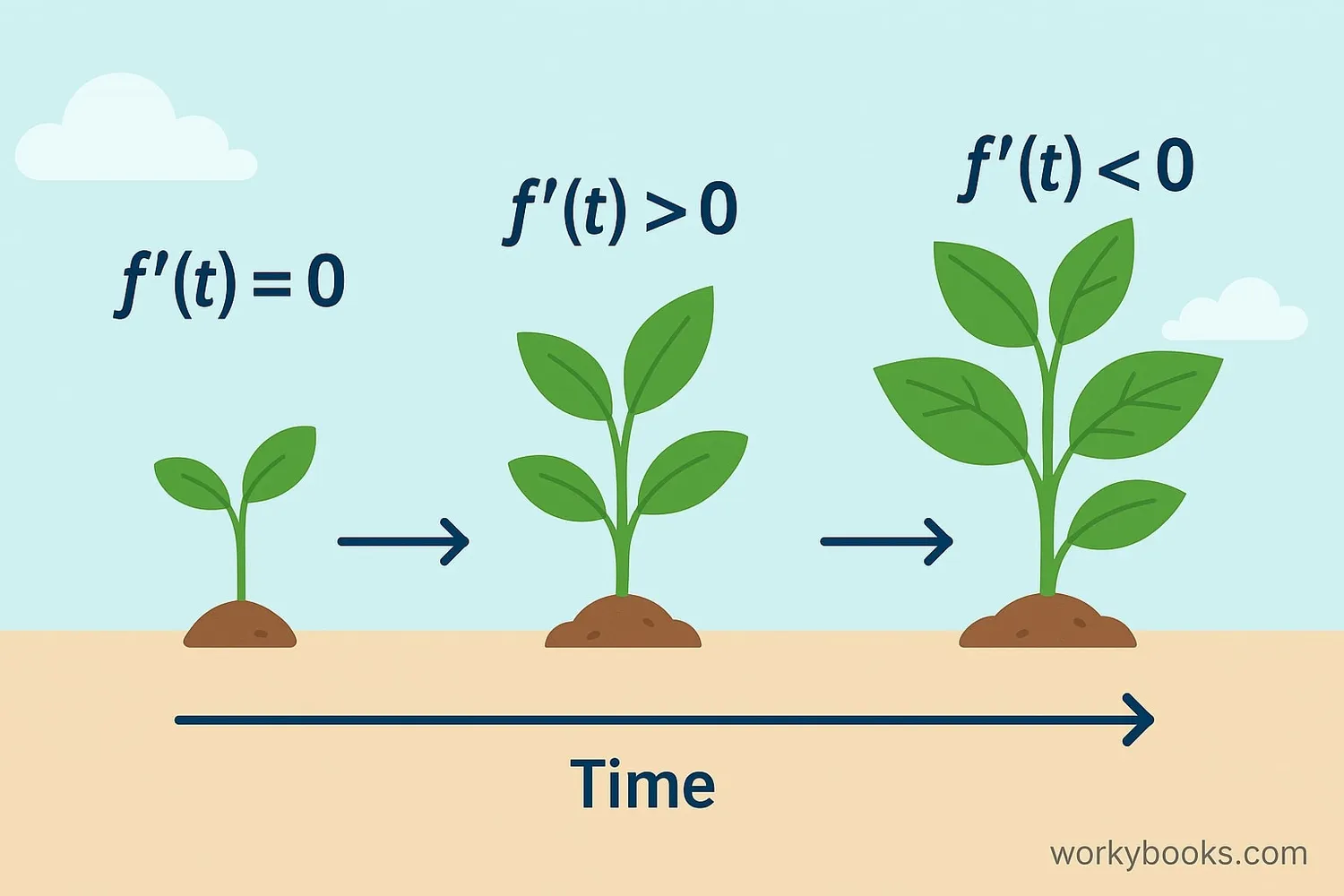
A differential equation is a special math tool that helps us understand how things change.
Think of it like a recipe that tells you how something grows, moves, or changes over time. For example:
- How a plant grows taller each day
- How water cools down after you take it off the stove
- How a ball rolls down a hill
These equations are different from regular math equations because they describe rates of change - how fast something is changing right now.
Key Concept
Differential equations are math tools that describe how things change. They help us predict future behavior based on current conditions.
How Differential Equations Work
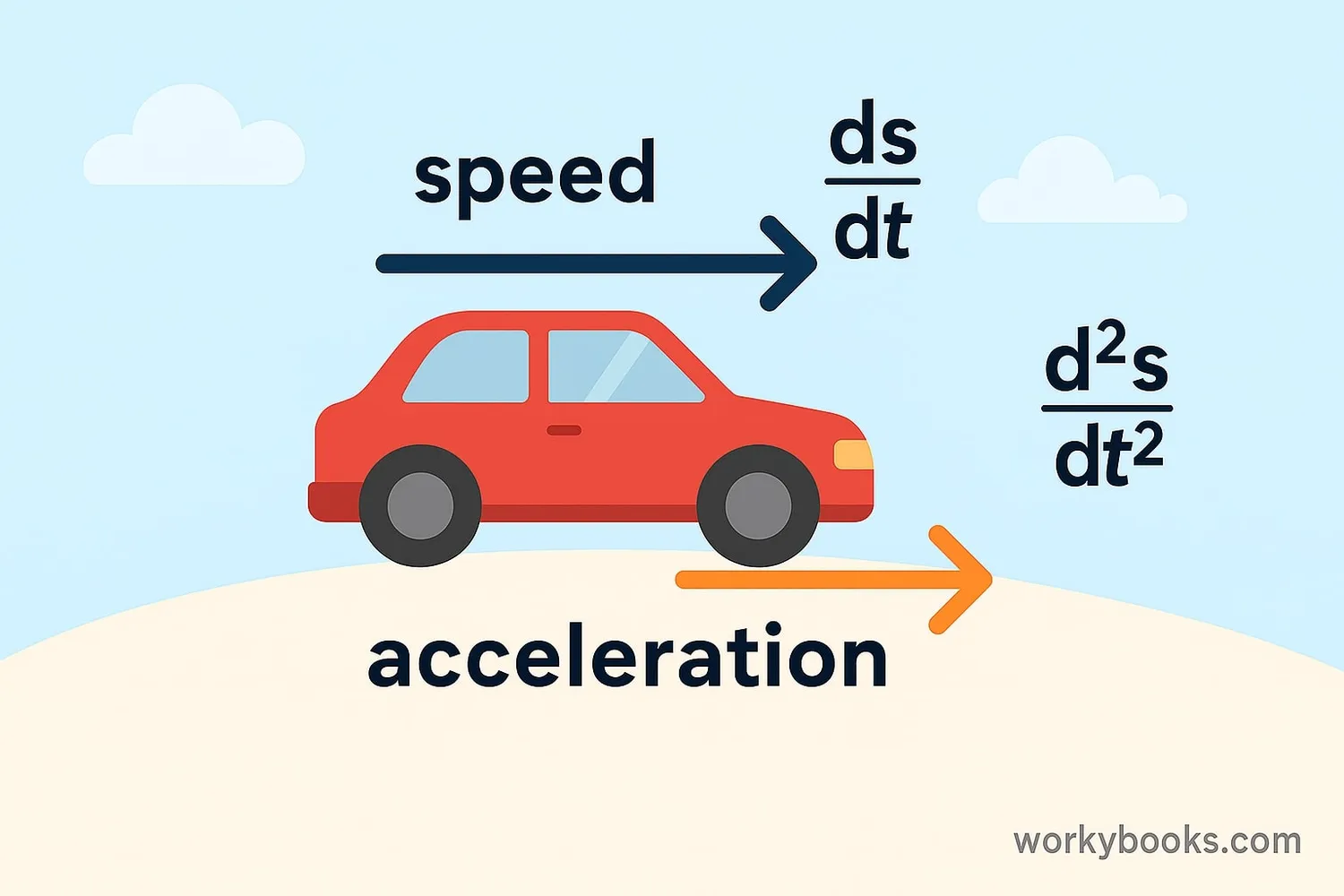
Differential equations use something called derivatives to describe change. A derivative measures how fast something is changing at a particular moment.
Simple Example
This equation says: "The speed at which something grows depends on how big it already is"
Example: A plant that doubles in size every week
Today: 10 cm tall
Next week: 20 cm tall
Following week: 40 cm tall
The differential equation for this plant would be: "The growth speed equals the current height times a constant number"
Remember
Derivatives are like speedometers - they tell you how fast something is changing right now, not how much it will change later.
Types of Differential Equations

There are two main types of differential equations:
1. Ordinary Differential Equations (ODEs)
These describe change in one dimension (like time). For example:
- How temperature changes over time
- How a population grows year by year
2. Partial Differential Equations (PDEs)
These describe change in multiple dimensions (like space and time). For example:
- How heat spreads through a metal plate
- How sound waves travel through air
While PDEs are more complex, both types help scientists and engineers understand our world.
| Type | Variables | Example |
|---|---|---|
| Ordinary (ODE) | One (usually time) | Plant growth |
| Partial (PDE) | Two or more | Heat distribution |
| Linear | Simple relationships | Spring motion |
| Nonlinear | Complex relationships | Weather patterns |
Did You Know?
The simplest differential equations can be solved with basic algebra, while complex ones require powerful computers!
Real-World Examples
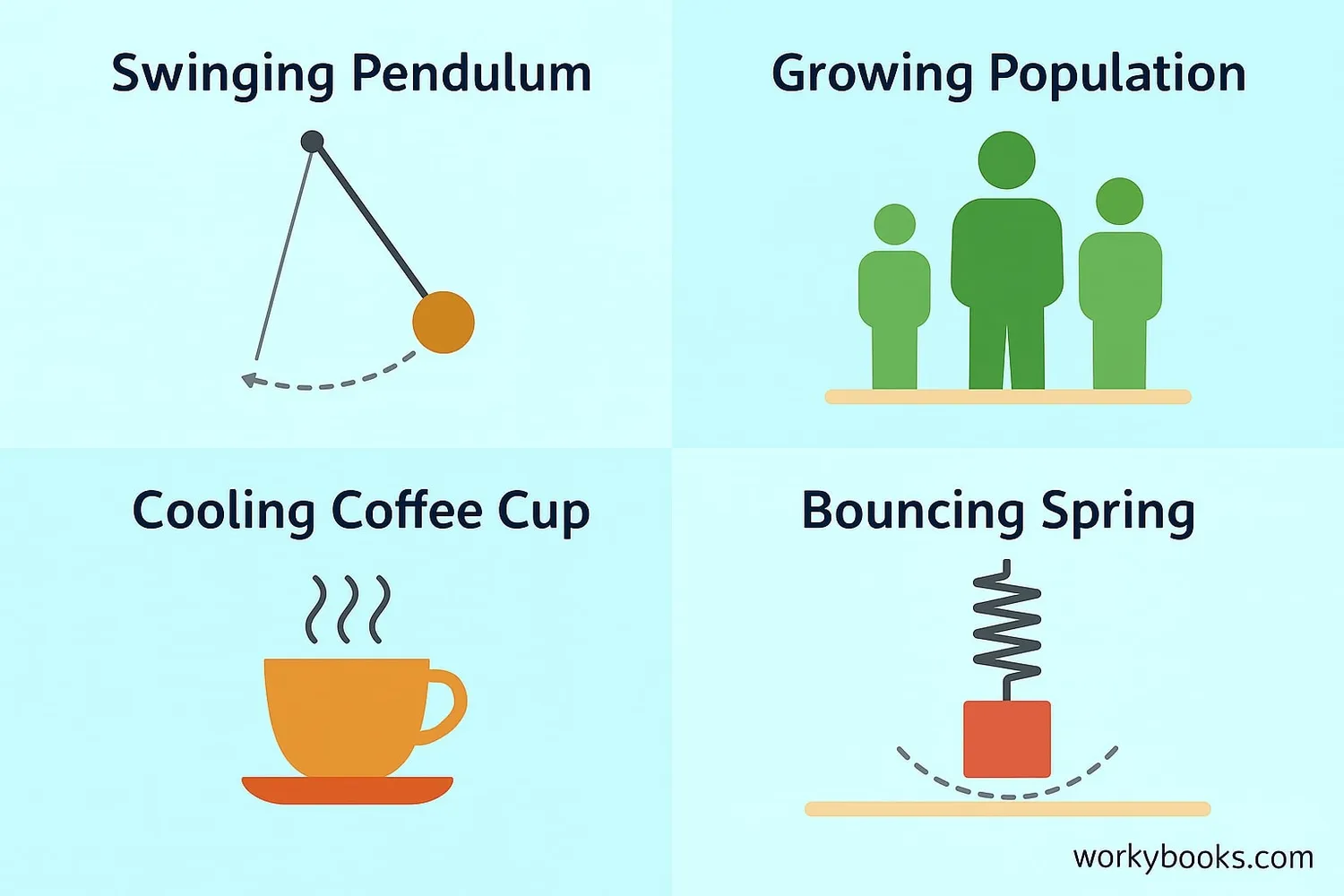
Differential equations help us understand many things in our world:
Example 1: Swinging Pendulum
The motion of a pendulum (like in a grandfather clock) follows a differential equation that describes how it swings back and forth.
Example 2: Population Growth
How animal populations grow in nature can be modeled with differential equations that consider birth rates and food supply.
Example 3: Cooling Objects
When you take cookies out of the oven, they cool down following Newton's law of cooling - a differential equation!
Example 4: Spring Motion
When you bounce on a trampoline, differential equations describe how the springs stretch and contract.
Real-World Connection
Engineers use differential equations to design safe bridges, cars, and airplanes that can handle different forces.
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about differential equations:
Math Trivia
Discover interesting facts about mathematics and equations:
Newton's Contribution
Sir Isaac Newton used differential equations to describe the motion of planets around the sun. His equations are still used by NASA today to plan space missions!
Predicting Weather
Meteorologists use differential equations to predict weather. A single weather forecast requires solving billions of differential equations on supercomputers!
Space Exploration
The Apollo missions to the moon used differential equations to navigate through space. These equations helped astronauts land precisely on the moon's surface.
Longest Equation
The longest differential equation ever solved filled over 200 pages! Mathematicians worked together for years to solve this equation about particle physics.


