Dilation in Geometry - Definition, Examples, Quiz, FAQ, Trivia
Learn how shapes change size without changing shape through dilation transformations
What is Dilation in Geometry?
Dilation is a special transformation in geometry that changes the size of a shape while keeping its proportions and angles exactly the same. It's like zooming in or out on a shape without changing its fundamental properties.
There are two key elements in every dilation:
Center of Dilation: This is the fixed point from which the dilation occurs. Imagine it as the anchor point that doesn't move while the shape grows or shrinks around it.
Scale Factor: This number tells us how much larger or smaller the shape becomes. It's the ratio between the size of the new shape (image) and the original shape (pre-image).
Key Concept
Dilation changes size but preserves shape. Angles stay the same, and sides become proportionally longer or shorter.
Understanding Scale Factor
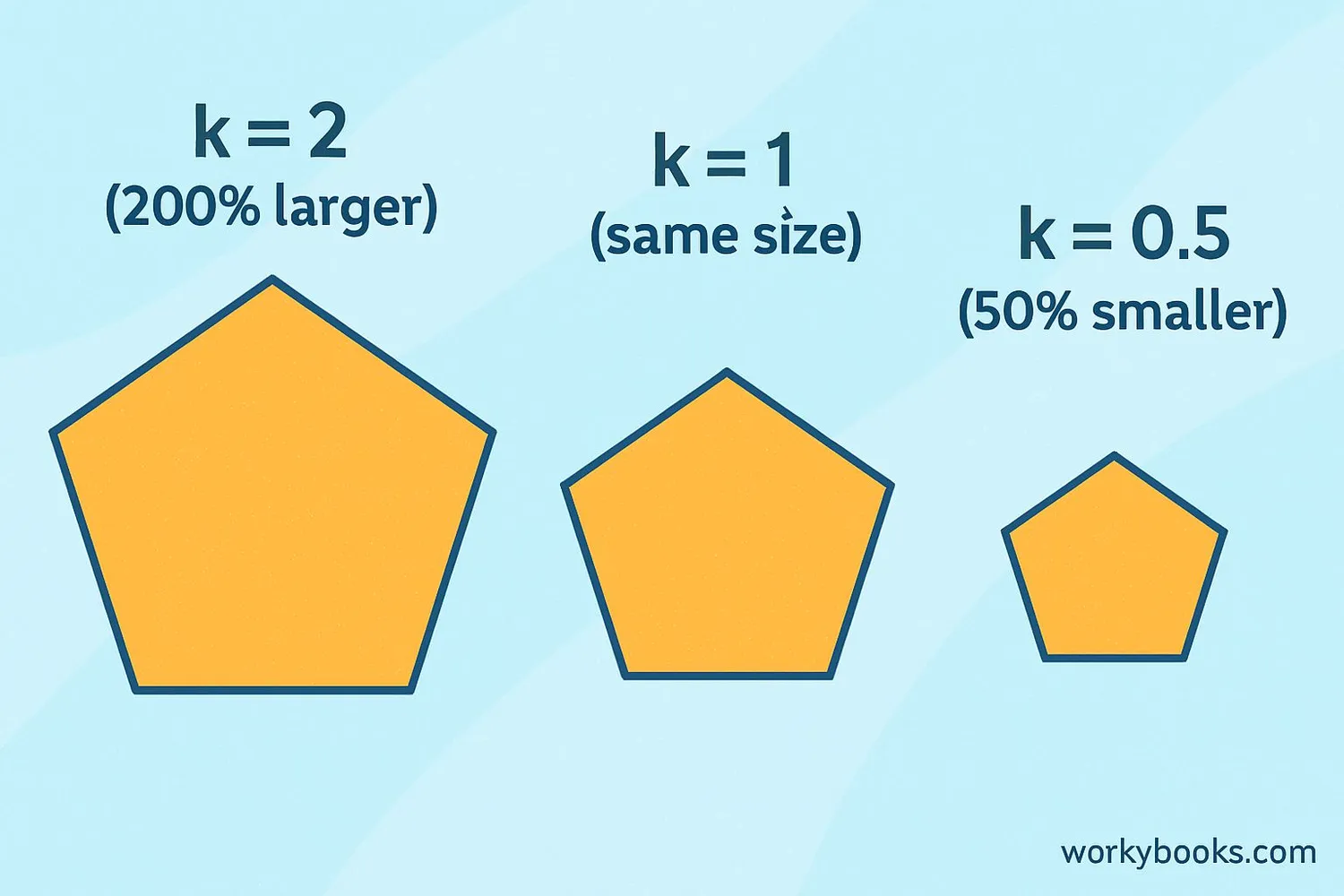
The scale factor (usually represented by k) determines whether the dilation makes the shape larger or smaller:
Scale Factor Formula
Reduction (0 < k < 1): When the scale factor is between 0 and 1, the shape becomes smaller. A scale factor of 0.5 means the new shape is half the size of the original.
Special Cases:
- If k = 1, the shape stays the same size
- If k = 0, the shape collapses to a single point (the center of dilation)
- If k is negative, the shape is dilated and reflected across the center
Remember
The scale factor affects all dimensions equally. If a shape doubles in size, both its width and height double.
How to Perform Dilation
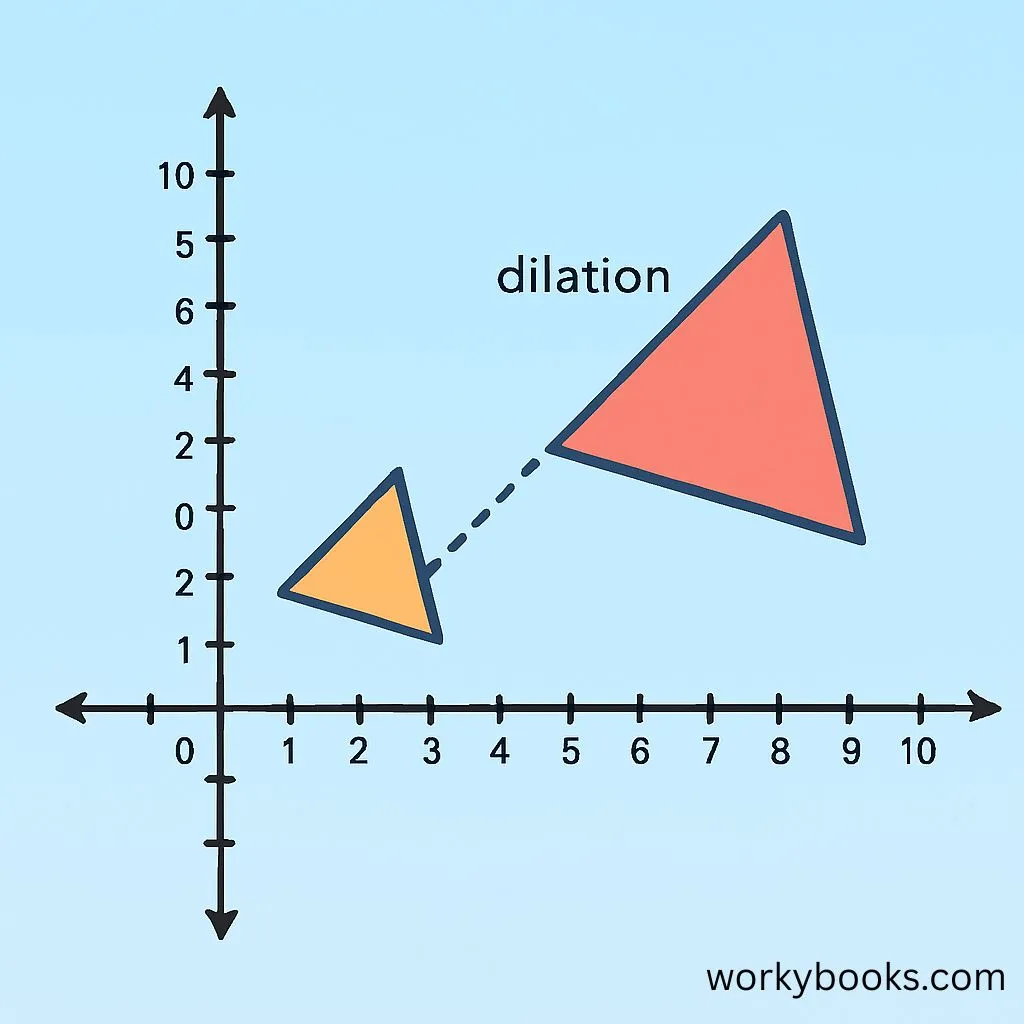
Performing dilation on a coordinate plane is straightforward when you follow these steps:
Step 1: Identify the center of dilation. This is our anchor point.
Step 2: Determine the scale factor (k).
Step 3: For each vertex of the shape:
- Measure the distance from the center of dilation to the vertex
- Multiply that distance by the scale factor
- Plot the new point at that distance from the center
Coordinate Dilation Formula
Where (h,k) is the center of dilation
Solution: Multiply each coordinate by 2 → A'(2,2), B'(6,2), C'(4,6)
Coordinate Tip
When dilating from the origin (0,0), simply multiply all coordinates by the scale factor.
Properties of Dilation
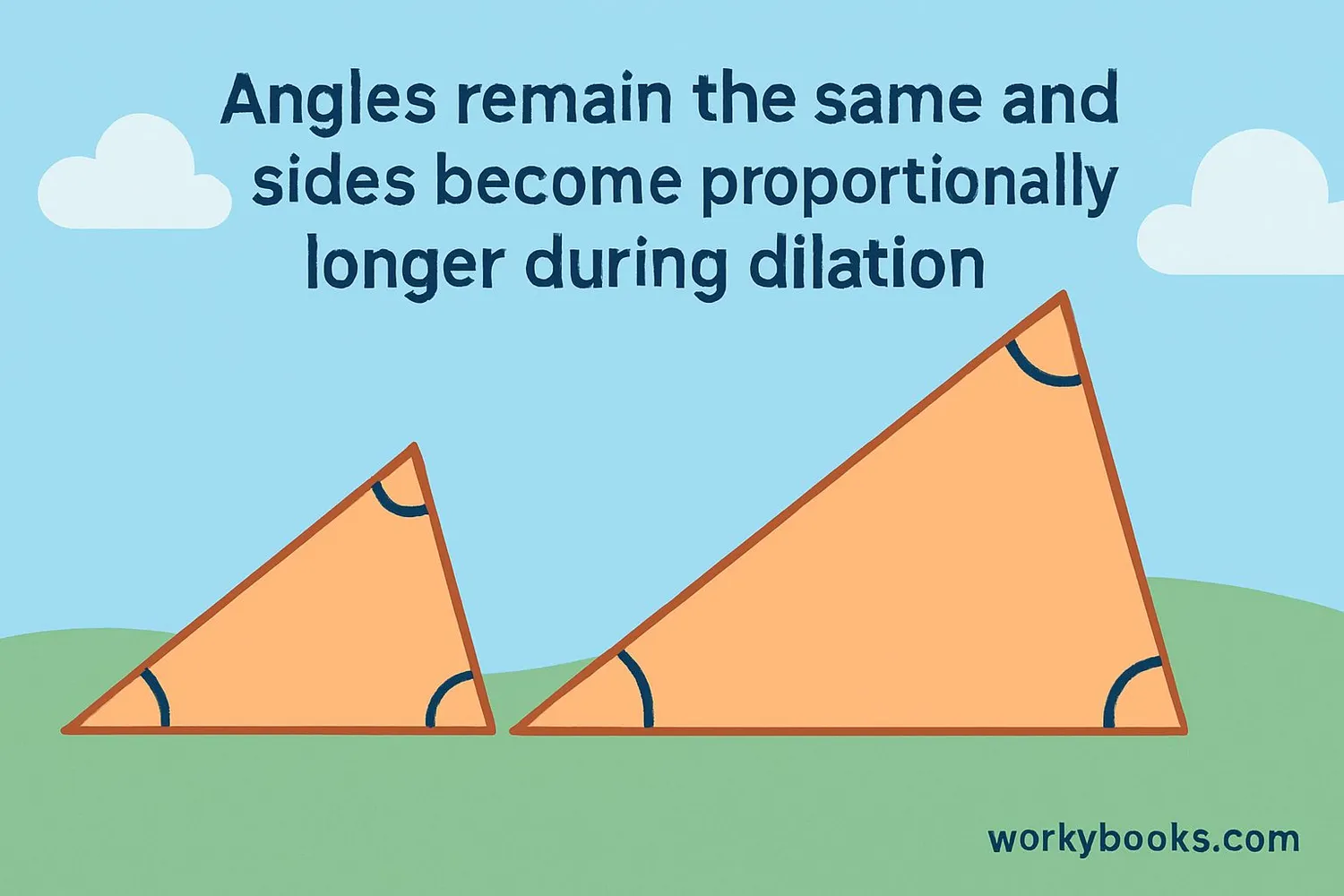
Dilation has several important mathematical properties that make it unique among transformations:
1. Angle Preservation: All angles in the shape remain exactly the same after dilation. A 90° angle stays 90°.
2. Parallelism: Lines that were parallel before dilation remain parallel afterward.
3. Proportionality: All sides change by the same scale factor. If one side becomes twice as long, all sides become twice as long.
4. Collinearity: Points that were on a straight line remain on a straight line after dilation.
5. Midpoint Preservation: The midpoint of a segment becomes the midpoint of the dilated segment.
These properties make dilation different from other transformations like rotation or reflection, which preserve size but may change position or orientation.
Important Note
Dilation is the only transformation that changes size while preserving shape. All other rigid transformations (translation, rotation, reflection) preserve both size and shape.
Real-World Examples of Dilation
Dilation isn't just a mathematical concept - it appears all around us in the real world:
1. Photography and Printing: When you enlarge or reduce a photo, you're applying dilation. The scale factor determines how much larger or smaller the image becomes.
2. Scale Models: Model cars, airplanes, and buildings are reductions of the real objects. A 1:24 scale model car has been dilated with a scale factor of 1/24.
3. Microscopy: When you look through a microscope, tiny objects appear larger. This is dilation with a scale factor greater than 1.
4. Maps and Blueprints: Maps represent large areas in a small space using reduction. The scale (like 1:100,000) tells us the dilation factor.
5. Shadow Proportions: Your shadow is a dilation of your silhouette. As you move closer to a light source, your shadow becomes larger (scale factor >1).
Real-World Connection
Movie special effects often use dilation principles when creating giant monsters or miniature sets!
Dilation Practice Quiz
Test your understanding of dilation with these 5 questions. Choose the correct answer for each.
Frequently Asked Questions
Here are answers to common questions about dilation:
Geometry Trivia
Discover interesting facts about dilation and geometry:
Ancient Origins
The concept of dilation dates back to ancient Greek mathematicians. Euclid described similar figures in his "Elements" around 300 BCE, establishing principles that form the basis of modern dilation concepts.
Fractal Geometry
Dilation is fundamental to fractal geometry. Fractals are shapes that look similar at different scales - a property called self-similarity that relies on repeated dilation transformations.
Astronomy Applications
Astronomers use dilation principles when studying celestial objects. Telescope images are often digitally dilated to make distant galaxies and nebulae easier to study and analyze.
Largest Scale Model
The Solar System model in Sweden is the world's largest scale model. The Sun is represented by a 110m diameter sphere, with planets placed up to 300km away, all using precise dilation ratios.





