Distance Between Point and Line - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate the shortest distance from a point to a line with simple explanations and practice activities
What is the Distance Between a Point and a Line?
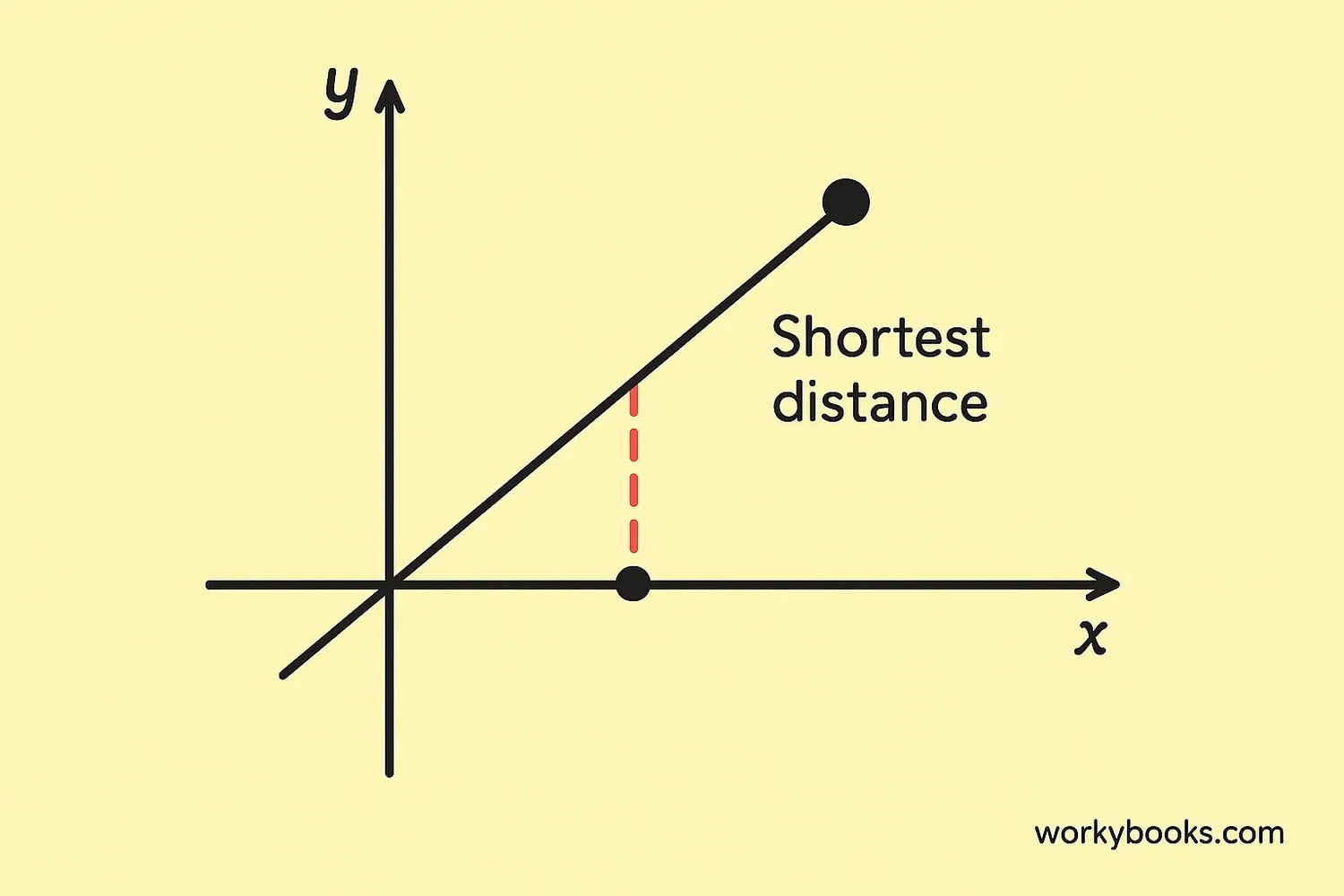
The distance between a point and a line is the length of the shortest path from the point to the line. This path is always perpendicular to the line.
Imagine you're standing at a point and want to walk to the nearest point on a straight road. The shortest path would be a straight line directly to the road, perpendicular to it. That perpendicular line represents the shortest distance.
This concept is important in many real-world situations, such as:
- Finding the shortest path to a road or wall
- Calculating distances in navigation systems
- Designing computer graphics and video games
- Solving geometry problems
Key Concept
The shortest distance between a point and a line is always measured along the perpendicular from the point to the line.
How to Calculate the Distance

To calculate the distance from a point to a line, we use a special formula. For a line given by the equation ax + by + c = 0 and a point (x₀, y₀), the distance is:
Distance Formula
Where d is the shortest distance from the point to the line.
- Write the line equation in the form ax + by + c = 0
- Identify the values of a, b, and c from the equation
- Identify the coordinates of the point (x₀, y₀)
- Plug into the formula and calculate the distance
Remember
The absolute value (| |) ensures the distance is always positive, and the denominator √(a² + b²) normalizes the line equation.
Examples
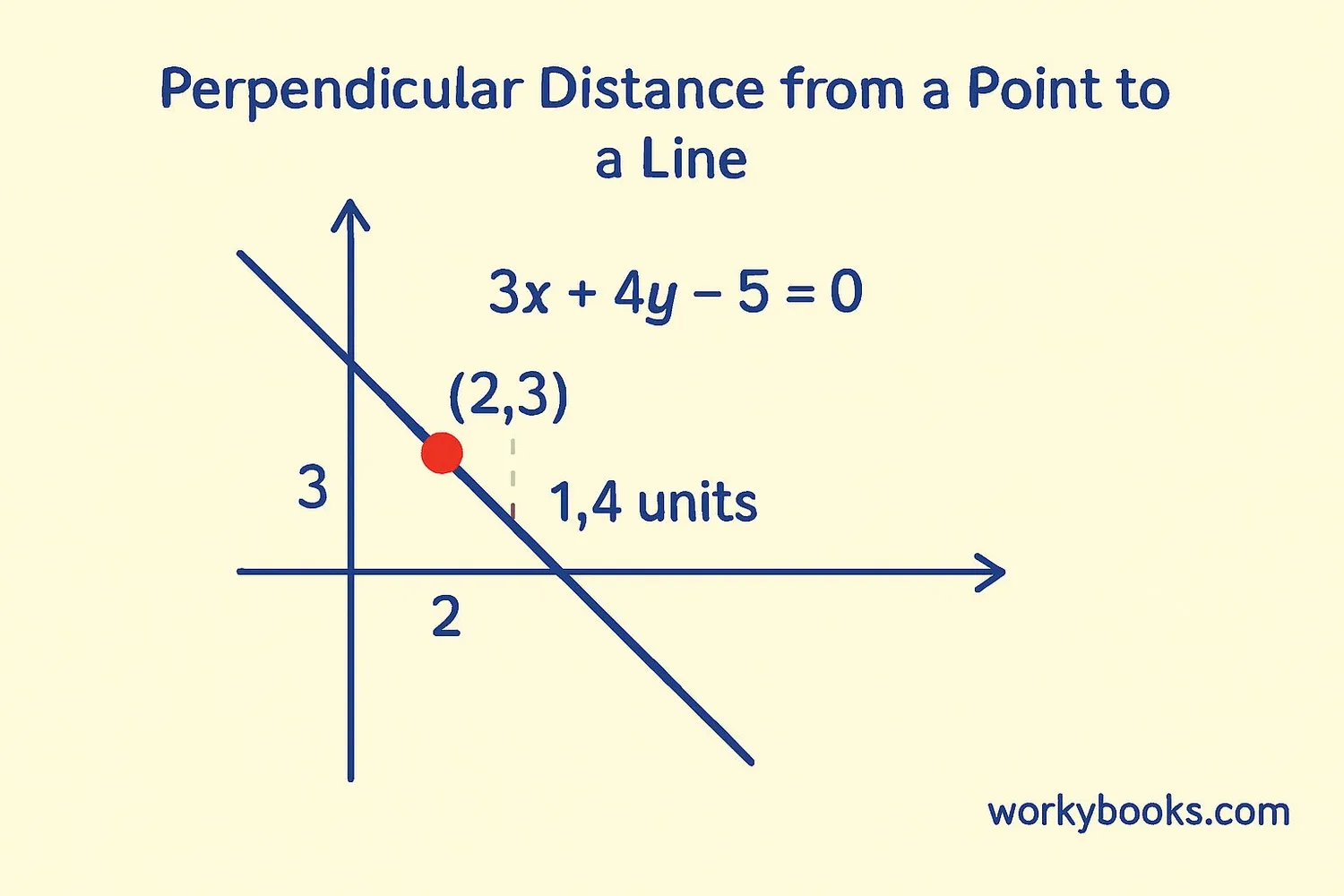
Let's practice with some examples:
Example 1
Find the distance from point (2,3) to the line 3x + 4y - 5 = 0
Example 2
Find the distance from point (1,1) to the line y = 2x + 1
Practice Tip
Always double-check that your line equation is in the standard form ax + by + c = 0 before using the formula.
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about distance between a point and a line:
Geometry Trivia
Discover interesting facts about geometry and distance:
Ancient Geometry
The concept of the shortest distance to a line was known to ancient Greek mathematicians. Euclid described perpendicular lines in his Elements around 300 BCE.
Everyday Geometry
When you use a GPS navigation system, it constantly calculates the shortest distance between your position (a point) and roads (lines) to provide accurate directions.
Space Applications
NASA uses distance formulas to calculate trajectories of spacecraft. The shortest distance to orbital paths helps determine optimal launch windows and fuel-efficient routes.
Geometry in Nature
Honeybees use geometric principles to build their hives with perfect hexagonal cells, minimizing wax usage while maximizing storage space - a natural optimization of distances.





