Distributive Property - Definition, Examples, Quiz, FAQ, Trivia
Learn how to distribute numbers in multiplication and addition with easy explanations and practice activities
What is the Distributive Property?

The Distributive Property is a math rule that helps us multiply a single number by a group of numbers added together. It tells us that:
a × (b + c) = (a × b) + (a × c)
Think of it like sharing or distributing something equally. If you have 3 bags, each containing 2 apples and 1 banana, you can distribute the bags to find you have 6 apples and 3 bananas total.
The Distributive Property is different from the Commutative Property (which says you can swap numbers: a+b = b+a) and the Associative Property (which says grouping doesn't matter: (a+b)+c = a+(b+c)). The Distributive Property combines multiplication with addition or subtraction.
Key Concept
The Distributive Property helps break down complex multiplication problems into simpler steps.
Distributive Property of Multiplication
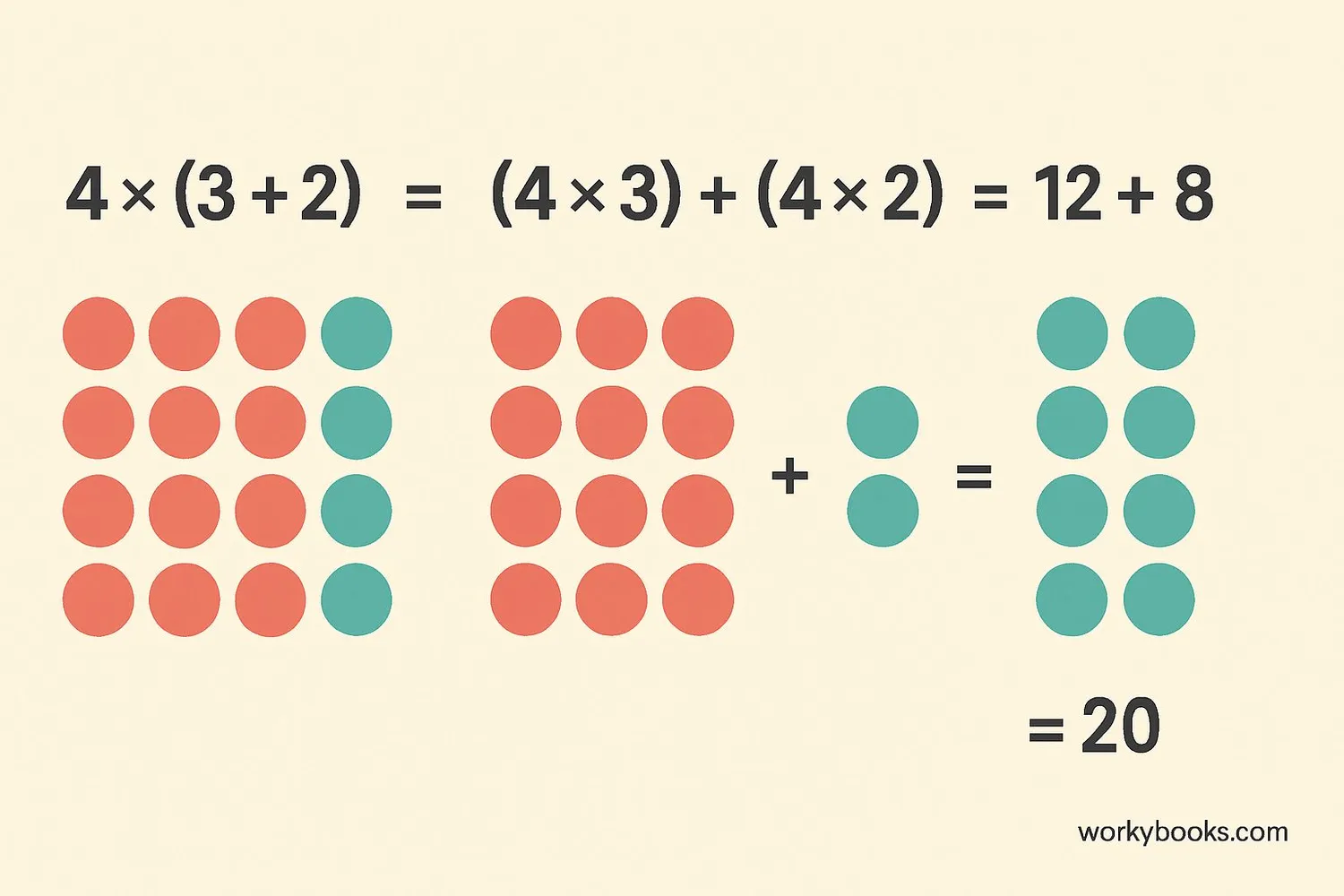
The Distributive Property of Multiplication is the most common form. It helps us multiply a number by a sum or difference inside parentheses.
Multiplication Formula
Example: 5 × (3 + 4)
Method 1: First add inside parentheses → 5 × 7 = 35
Method 2: Use distributive property → (5 × 3) + (5 × 4) = 15 + 20 = 35
Both methods give the same answer! The distributive property gives us a different way to solve problems.
Example 1
4 × (6 + 3) = (4 × 6) + (4 × 3) = 24 + 12 = 36
Example 2
7 × (10 - 2) = (7 × 10) - (7 × 2) = 70 - 14 = 56
Distributive Property of Division

The Distributive Property also works with division over addition and subtraction. It helps us divide a sum or difference by a number.
Division Formula
Example: (12 + 18) ÷ 6
Method 1: First add inside parentheses → 30 ÷ 6 = 5
Method 2: Use distributive property → (12 ÷ 6) + (18 ÷ 6) = 2 + 3 = 5
Both methods give the same answer! The distributive property gives us flexibility in solving problems.
Distributive Property with Integers
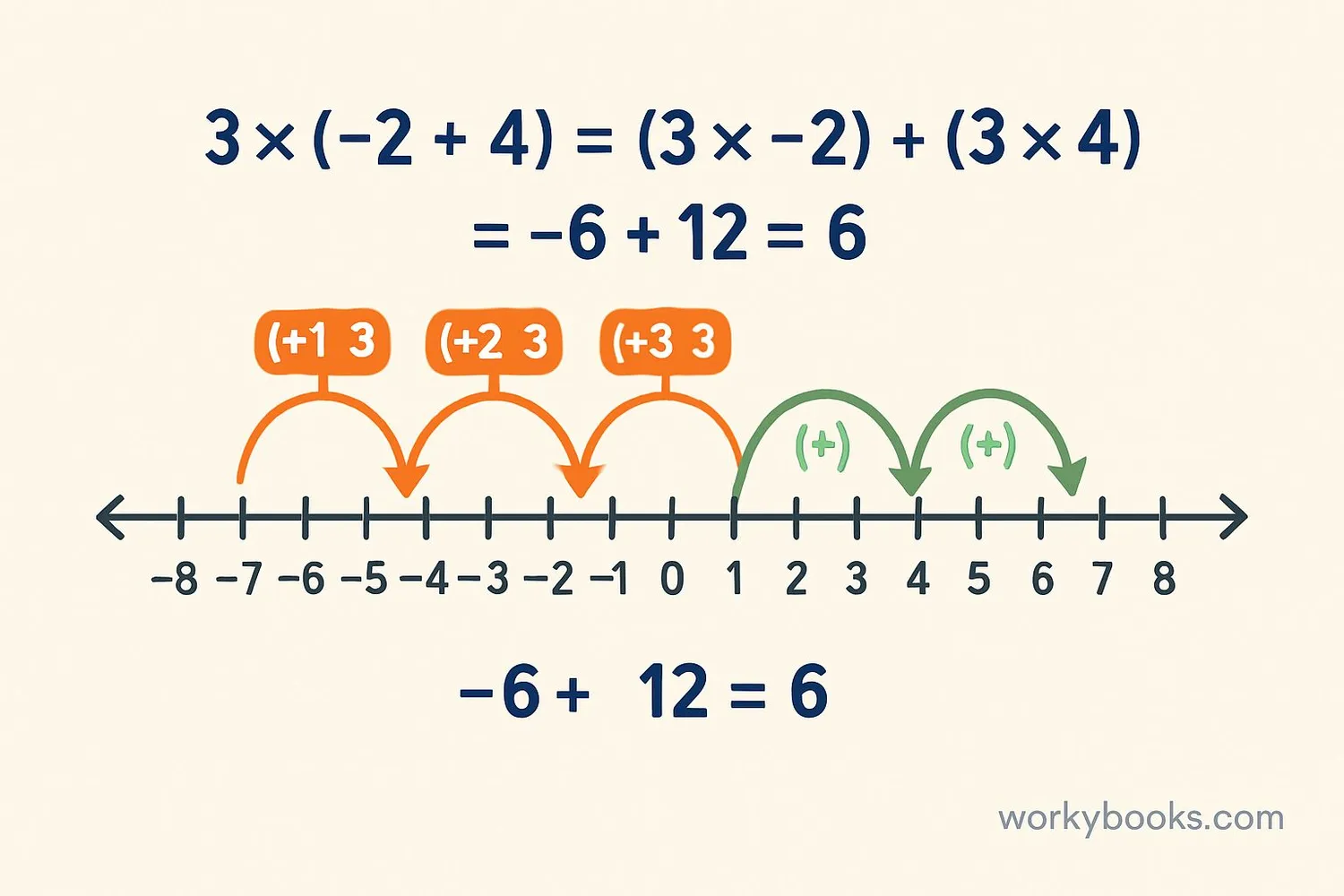
The Distributive Property works with both positive and negative numbers (integers). When distributing a negative number, remember to distribute the negative sign to each term inside the parentheses.
With Negative Numbers
Example: -4 × (3 + 5)
Without distributive: -4 × 8 = -32
With distributive: (-4 × 3) + (-4 × 5) = -12 + (-20) = -32
Example with subtraction: 5 × (7 - 2)
Without distributive: 5 × 5 = 25
With distributive: (5 × 7) - (5 × 2) = 35 - 10 = 25
Remember
When distributing a negative number, all terms inside the parentheses change their signs.
Simplifying Expressions
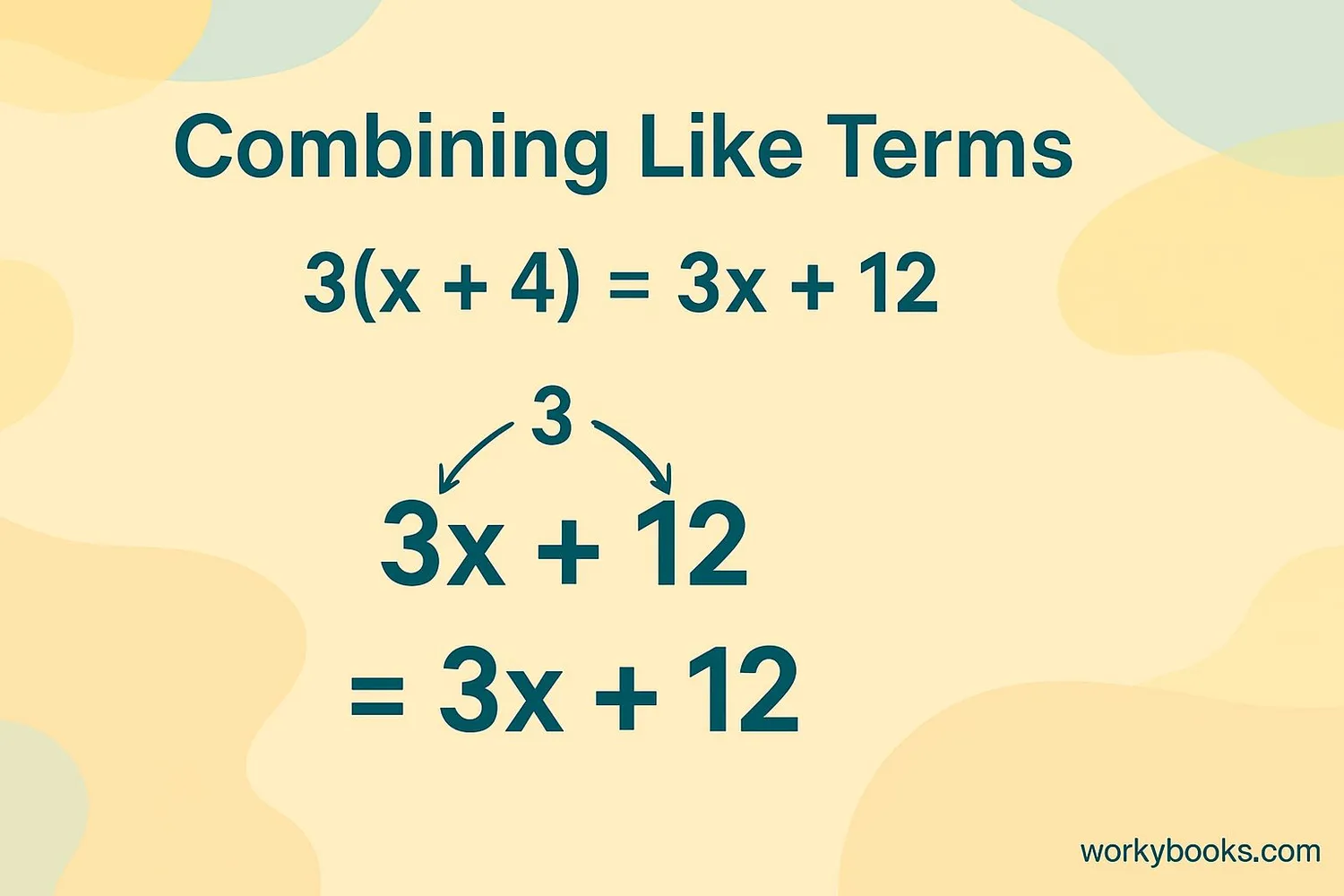
The Distributive Property is especially helpful for simplifying algebraic expressions and combining like terms.
Simplifying Polynomials: We use the distributive property to multiply a term by a polynomial (an expression with multiple terms).
Example: Simplify 3(x + 4)
Solution: 3 × x + 3 × 4 = 3x + 12
Combining Like Terms: After distributing, we can combine terms that have the same variable part.
Example: Simplify 2(3x + 5) + 4(x - 2)
Step 1: Distribute → 6x + 10 + 4x - 8
Step 2: Combine like terms → (6x + 4x) + (10 - 8) = 10x + 2
Example 1
4(2x + 3) = 8x + 12
Example 2
5(y - 2) + 3(2y + 1) = 5y - 10 + 6y + 3 = 11y - 7
Solving Equations with Distributive Property
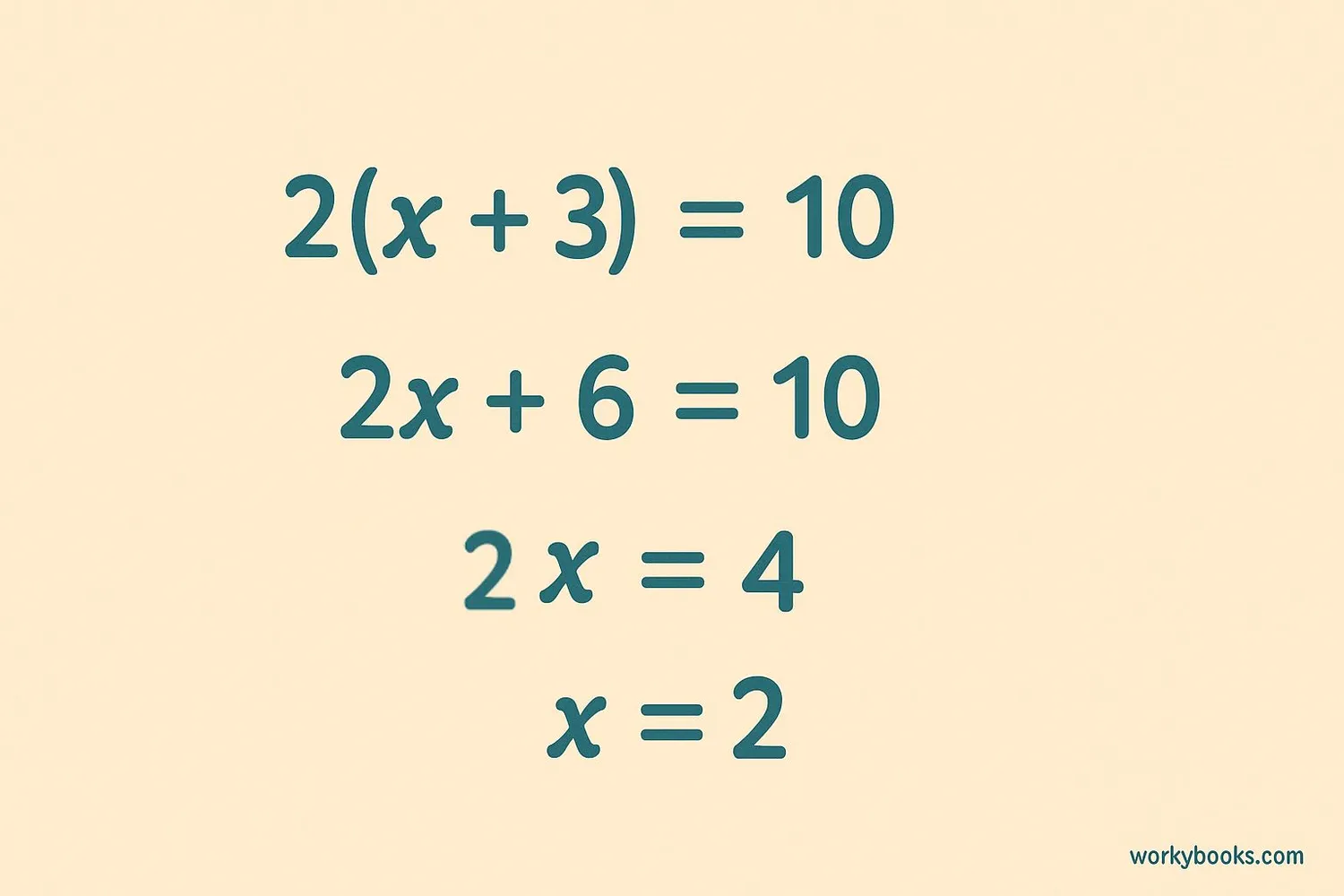
The Distributive Property helps us solve equations where a number is multiplied by an expression in parentheses.
Steps to solve:
- Apply the distributive property to remove parentheses
- Combine like terms on each side of the equation
- Use inverse operations to isolate the variable
- Check your solution
Step 1: Distribute → 2x + 6 = 10
Step 2: Subtract 6 from both sides → 2x = 4
Step 3: Divide both sides by 2 → x = 2
Step 4: Check → 2(2 + 3) = 2(5) = 10 ✓
The Distributive Property works with the Order of Operations (PEMDAS) to help solve equations efficiently.
Distributive Property Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the distributive property:
Math Trivia
Discover interesting facts about math and the distributive property:
Ancient Origins
The distributive property was first described by the ancient Greek mathematician Euclid around 300 BC in his work "Elements," which is one of the most influential works in mathematics history.
Everyday Math
We use the distributive property in everyday situations without realizing it! When calculating total costs (like 3 items at $2 each and 3 items at $3 each), we're using the distributive property.
Algebraic Foundation
The distributive property is essential for algebra. It allows us to multiply polynomials, factor expressions, and solve equations - skills that are foundational for higher mathematics and science.
Computer Science
In computer science, the distributive property helps optimize calculations. Computers use it to simplify complex operations and make computations faster, especially in graphics processing and algorithms.





