Factors in Math - Definition, Examples, Quiz, FAQ, Trivia
Learn how numbers work together with easy explanations, visual examples, and practice activities
What is a Factor?

A factor is a number that divides exactly into another number without leaving a remainder. Factors are numbers you multiply together to get another number.
Think of factors as the building blocks of numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because:
1 × 12 = 12
2 × 6 = 12
3 × 4 = 12
Every number has at least two factors: 1 and itself. Numbers with exactly two factors (1 and themselves) are called prime numbers.
Key Concept
Factors are whole numbers that multiply together to make another number. For example, 3 and 4 are factors of 12 because 3 × 4 = 12.
How to Find Factors
Finding factors is like being a number detective! Here's how you do it:
1. Start with the number you want to factor (like 24)
2. Begin with 1 and check if it divides evenly into 24 (1 × 24 = 24)
3. Then try 2 (2 × 12 = 24)
4. Then try 3 (3 × 8 = 24)
5. Then try 4 (4 × 6 = 24)
6. Then try 5 - but 24 ÷ 5 = 4.8 (not whole, so not a factor)
7. Stop when you reach a number you've already found (like 6 which we already have with 4)
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, and 24
Factor Finding Tip
You only need to check numbers up to the square root of the number you're factoring!
Properties of Factors

Factors have some special properties that make them interesting:
1. Universal Factor: The number 1 is a factor of every whole number.
2. Self Factor: Every number is a factor of itself.
3. Factor Pairs: Factors always come in pairs that multiply to make the number.
4. Limited Factors: Prime numbers have exactly two factors (1 and themselves).
5. Abundant Factors: Composite numbers have more than two factors.
Here's a visual representation of different types of numbers:
Remember
Prime numbers are like the atoms of mathematics - they can't be broken down into smaller whole number factors!
Factor Examples

Let's look at some examples to understand factors better:
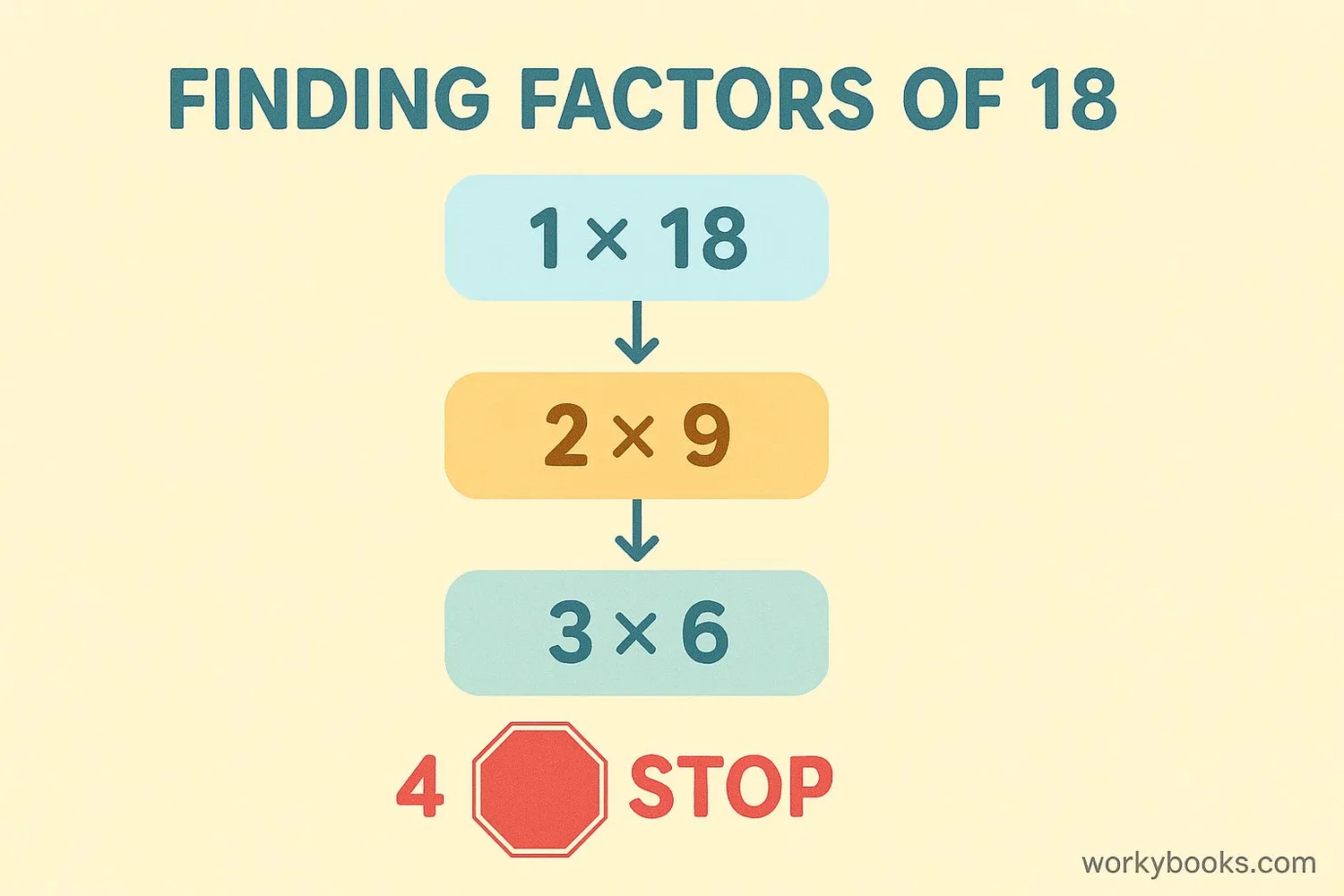
Example 1: Find factors of 18
Solution: 1 × 18 = 18
2 × 9 = 18
3 × 6 = 18
So factors are: 1, 2, 3, 6, 9, 18
Example 2: Find factors of 7
Solution: 1 × 7 = 7
Only 1 and 7 divide evenly into 7
So 7 is a prime number with factors: 1 and 7
Example 3: Find factor pairs of 30
Solution: 1 × 30 = 30
2 × 15 = 30
3 × 10 = 30
5 × 6 = 30
So factor pairs are: (1,30), (2,15), (3,10), (5,6)
Common Factors
Sometimes two numbers share common factors. For example, 12 and 18 share these factors: 1, 2, 3, and 6. The greatest common factor (GCF) is the largest factor they share - in this case, 6.
Math Tip
When finding factors, start with 1 and work your way up. Write down each pair as you find them to stay organized!
Factor Practice Quiz
Test your factor knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about factors:
Math Factor Trivia
Discover interesting facts about factors and numbers:
Ancient Factorization
The ancient Greeks studied factors over 2,000 years ago. Euclid's "Elements" written around 300 BC contains important discoveries about prime numbers and factors.
Factor Superhero
The number 60 has 12 factors (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60), more than any smaller number. This makes it very useful for dividing things like time (60 seconds in a minute) and circles (360 degrees).
Prime Protection
Large prime numbers are used to keep internet communications secure. Their special factor properties (only divisible by 1 and themselves) make them perfect for creating codes that are hard to break!
Perfect Numbers
A perfect number equals the sum of its proper factors (factors excluding itself). 6 is perfect because 1 + 2 + 3 = 6. The next perfect number is 28 (1 + 2 + 4 + 7 + 1 4 = 28).


