Fundamental Theorem of Arithmetic - Definition, Examples, Quiz, FAQ, Trivia
Learn about prime factorization and how every number has a unique prime factorization
What is the Fundamental Theorem of Arithmetic?
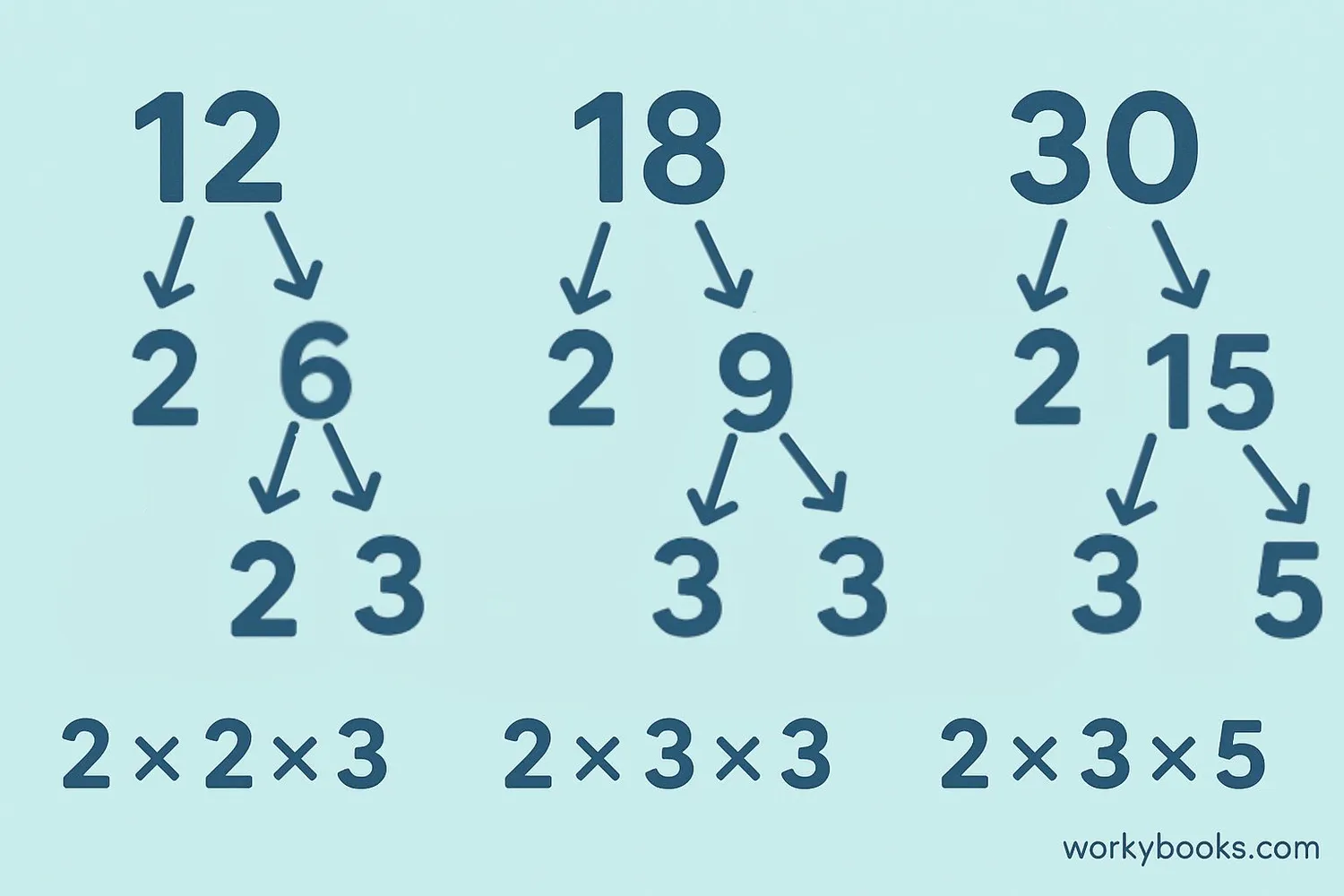
The Fundamental Theorem of Arithmetic is an important rule in mathematics that tells us that every whole number greater than 1 is either a prime number itself or can be written as a unique product of prime numbers. This is called the number's prime factorization.
Think of it like this: just as every building is made from basic building blocks (like bricks), every number is made from basic "number building blocks" called prime numbers.
The theorem has two important parts:
1. Every number greater than 1 can be expressed as a product of primes.
2. This prime factorization is unique - no other combination of primes will give you the same number.
Key Concept
Just as every Lego creation can be broken down into basic bricks, every number can be broken down into prime numbers in only one way.
Prime Factorization
Prime factorization is the process of breaking down a composite number into its prime factors. A prime number is a number greater than 1 that has no positive divisors other than 1 and itself. A composite number is a number that has more than two factors.
There are different methods to find the prime factorization of a number:
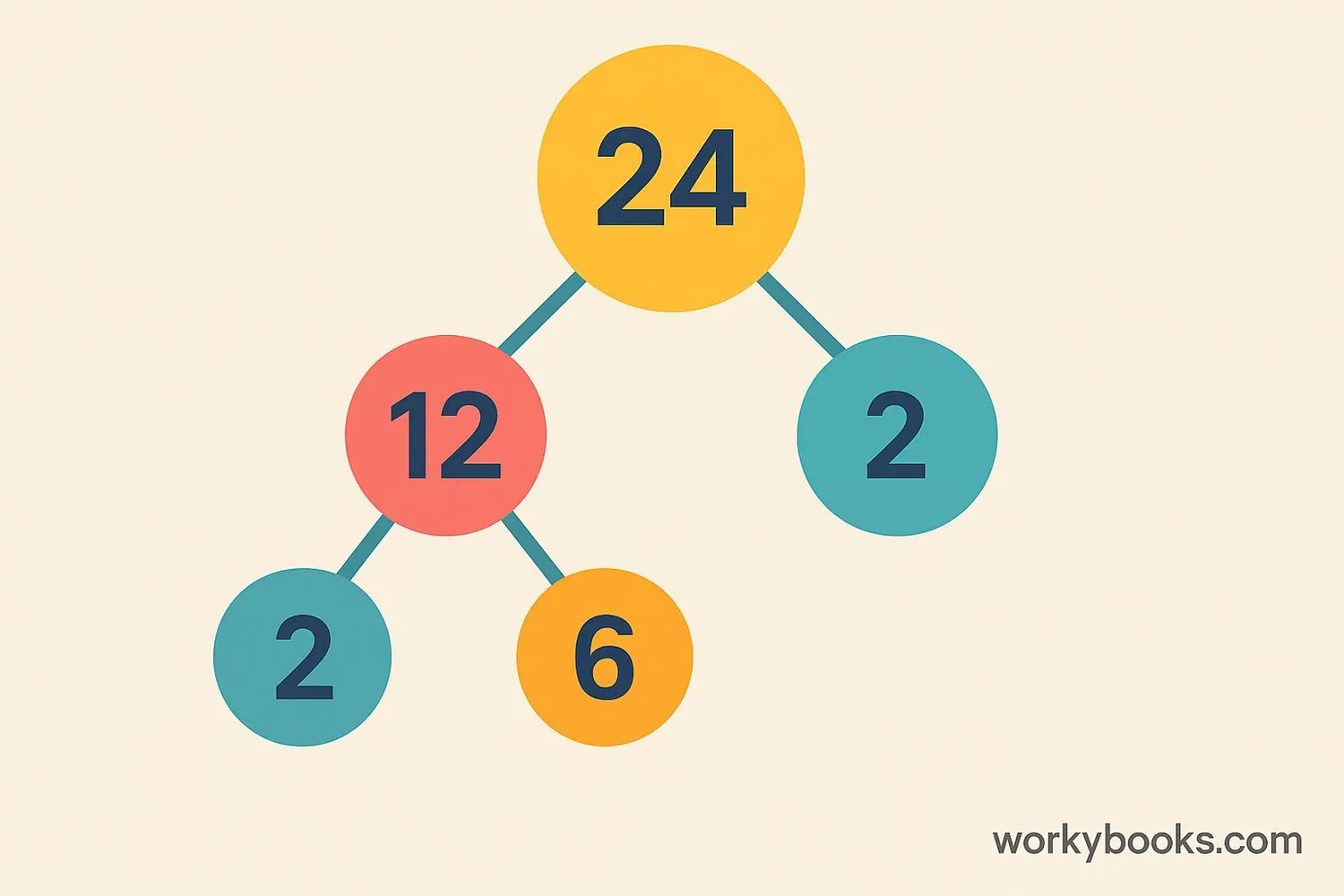
Factor Tree Method: We break down the number into factors until all factors are prime numbers.
Division Method: We divide the number by prime numbers until the quotient is 1.
Remember
No matter which method you use or which factors you start with, you'll always end up with the same prime factors for any given number.
Examples of Prime Factorization
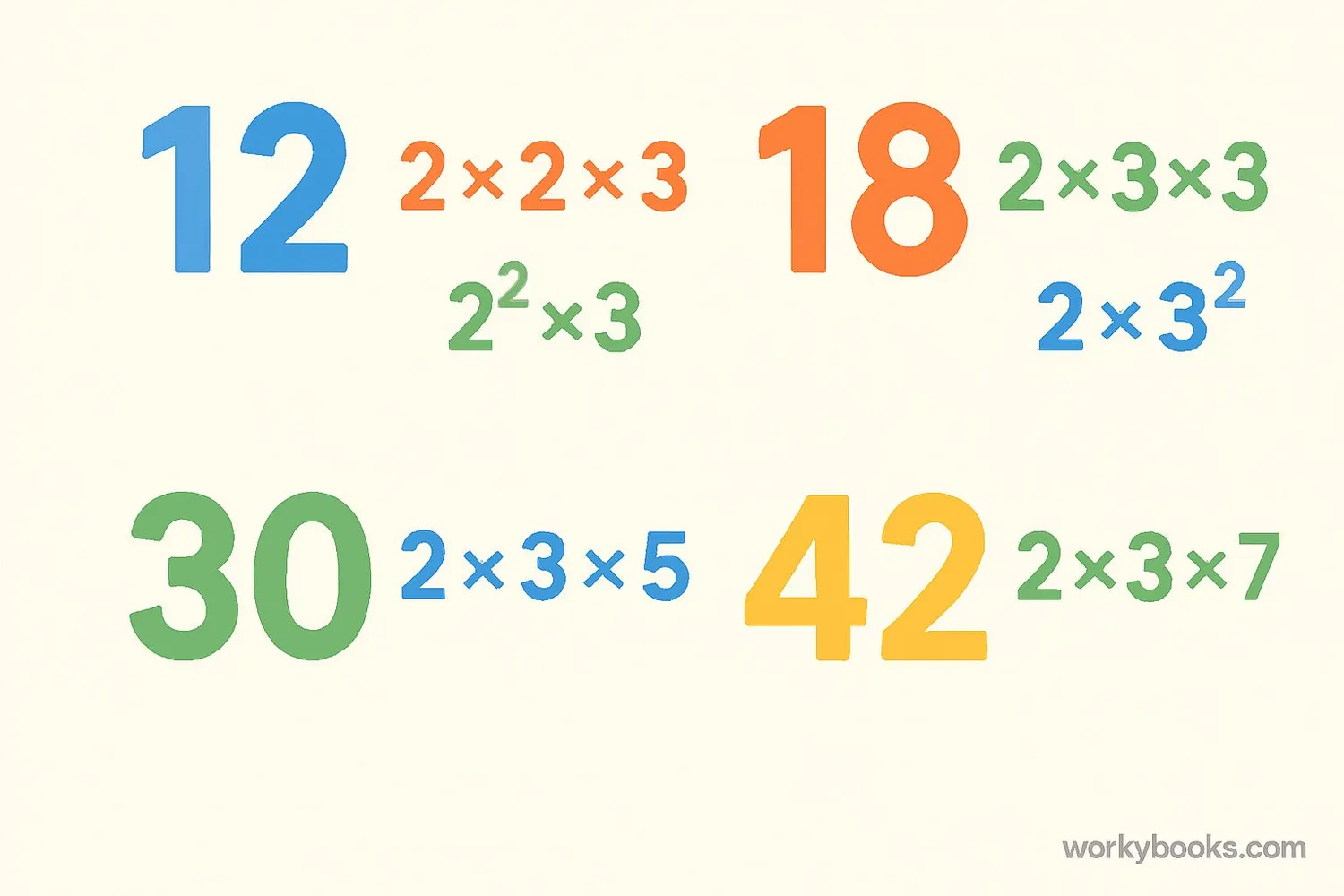
Let's look at some examples of prime factorization:
Example 1: Find the prime factorization of 12
Solution: 12 = 2 × 2 × 3 = 2² × 3
Example 2: Find the prime factorization of 18
Solution: 18 = 2 × 3 × 3 = 2 × 3²
Example 3: Find the prime factorization of 30
Solution: 30 = 2 × 3 × 5
Example 4: Find the prime factorization of 42
Solution: 42 = 2 × 3 × 7
Notice that in each case, no matter how we break down the number, we always end up with the same prime factors. This demonstrates the uniqueness part of the Fundamental Theorem of Arithmetic.
| Number | Prime Factorization | Exponential Form |
|---|---|---|
| 12 | 2 × 2 × 3 | 2² × 3 |
| 18 | 2 × 3 × 3 | 2 × 3² |
| 24 | 2 × 2 × 2 × 3 | 2³ × 3 |
| 30 | 2 × 3 × 5 | 2 × 3 × 5 |
| 36 | 2 × 2 × 3 × 3 | 2² × 3² |
| 42 | 2 × 3 × 7 | 2 × 3 × 7 |
| 60 | 2 × 2 × 3 × 5 | 2² × 3 × 5 |
Practice Tip
Try creating factor trees for different numbers. You'll discover that no matter which factors you start with, you'll always end up with the same prime factors!
Practice Quiz
Test your understanding of the Fundamental Theorem of Arithmetic with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about the Fundamental Theorem of Arithmetic:
Number Trivia
Discover interesting facts about numbers and prime factorization:
Infinite Primes
There are infinitely many prime numbers. This was first proven by the ancient Greek mathematician Euclid over 2,000 years ago!
Largest Known Prime
The largest known prime number (as of 2023) is 282,589,933 − 1. It has 24,862,048 digits and would take over 4,000 pages to write out!
Fundamental in Math
The Fundamental Theorem of Arithmetic is so important that it's sometimes called the "Unique Factorization Theorem" or the "Unique Prime Factorization Theorem."
Used in Secret Codes
Prime factorization is used in cryptography (secret codes) to keep information secure. The difficulty of factoring large numbers is what makes modern encryption work.


