Hemisphere Shape - Definition, Examples, Quiz, FAQ, Trivia
Learn about half-spheres with easy explanations, properties, formulas, and practice activities
What is a Hemisphere?
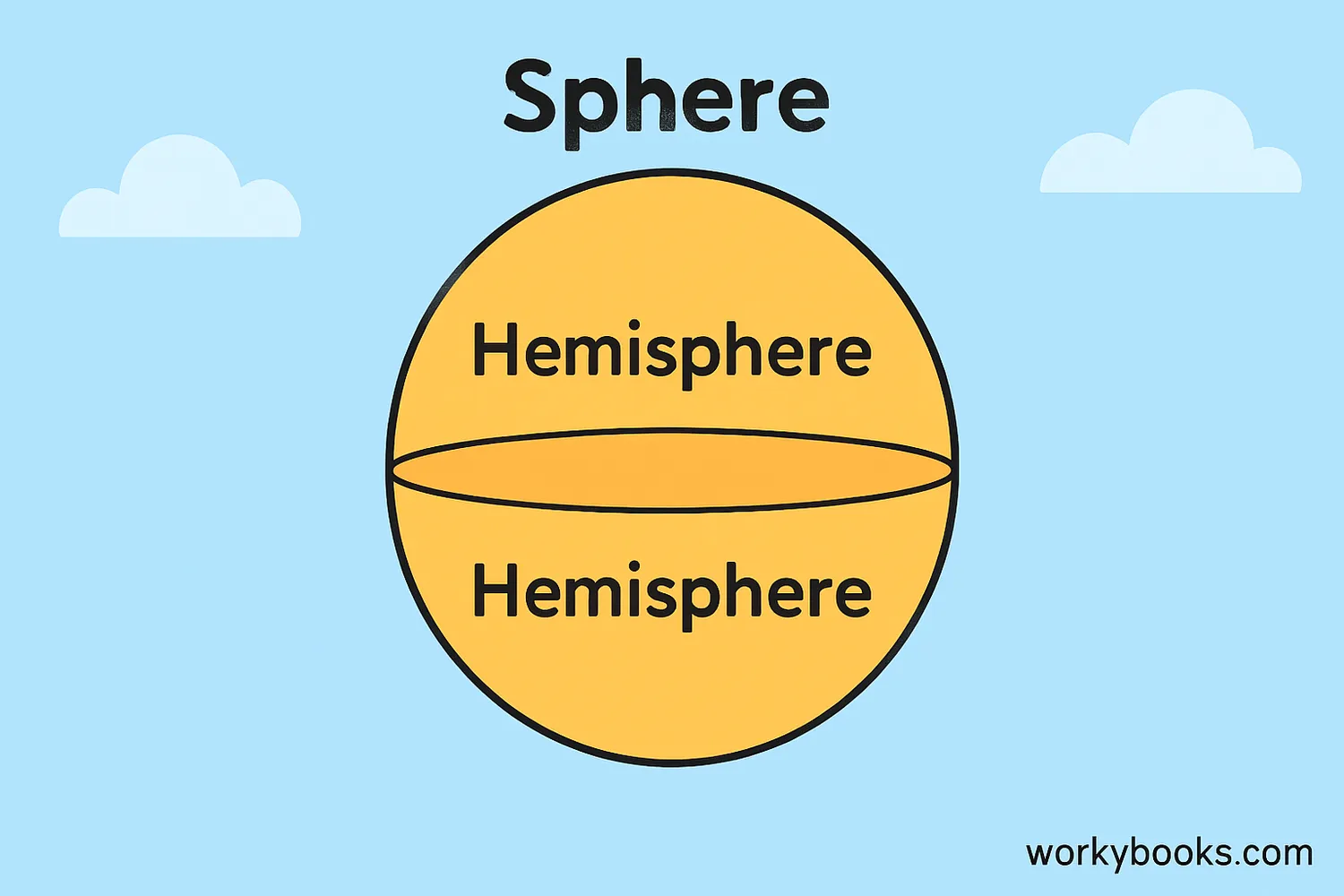
A hemisphere is a 3D shape that is exactly half of a sphere. The word "hemisphere" comes from two Greek words: "hemi" meaning half and "sphaira" meaning sphere.
Just like cutting an orange or a melon exactly in half, each piece is a hemisphere. Hemispheres are all around us in everyday life - from bowls and domes to the northern and southern halves of our planet Earth.
A hemisphere has one flat circular face (where it was cut from the sphere) and one curved face. Understanding hemispheres helps us understand how 3D shapes work and how to calculate their measurements.
Key Concept
A hemisphere is half of a sphere. It has one flat circular face and one curved face.
Properties of a Hemisphere
Hemispheres have special properties that help us identify and work with them:
| Property | Description |
|---|---|
| Faces | 2 faces (1 flat circular face, 1 curved face) |
| Edges | 1 circular edge where the flat and curved surfaces meet |
| Vertices | No vertices (corners) |
| Symmetry | Rotational symmetry around the central axis |
| Flat Face | A circle with the same radius as the original sphere |
| Curved Surface | Exactly half the surface area of a full sphere |
Remember
The flat face of a hemisphere is always a circle, and its radius is the same as the radius of the original sphere.
Hemisphere Formulas
We can calculate the volume and surface area of a hemisphere using mathematical formulas. Since a hemisphere is half of a sphere, we use the sphere formulas and then divide by 2.
Volume Formula
Where V is volume, π is pi (approximately 3.14), and r is the radius.
Total Surface Area Formula
Where A is total surface area, π is pi, and r is the radius.
Curved Surface Area Formula
This is just the curved part of the hemisphere (half of a sphere's surface area).
Formula Tip
Remember that the volume of a hemisphere is 2/3 of the volume of a cylinder with the same radius and height.
Real-World Examples
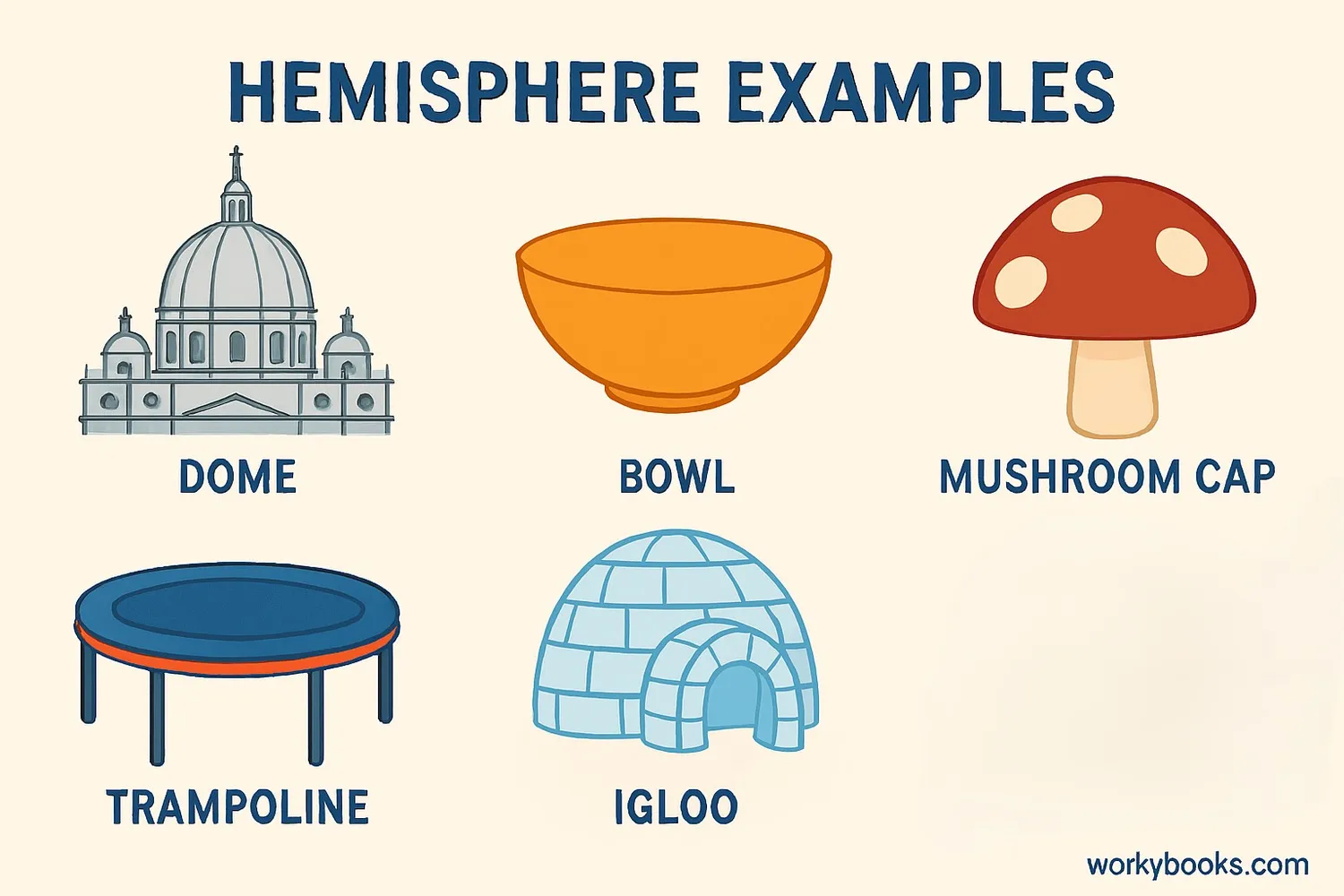
Hemispheres appear in many places in our world. Here are some common examples:
Human-Made Hemispheres
- Domes: Many buildings have dome-shaped roofs that are hemispheres
- Bowls: Most bowls are hemisphere-shaped
- Igloos: Traditional snow houses are built in a hemisphere shape
- Planetariums: The projection screens are often hemispheres
Natural Hemispheres
- Mushroom caps: Many mushrooms have hemisphere-shaped tops
- Nests: Some bird nests are hemisphere-shaped
- Rock formations: Some eroded rocks form natural hemispheres
- Half-fruits: When you cut round fruits in half, they form hemispheres
Practice Example
Let's say we have a hemisphere with a radius of 5 cm. Let's calculate its volume and surface area:
Volume: V = (2/3) × π × r³ = (2/3) × 3.14 × (5 × 5 × 5) = (2/3) × 3.14 × 125 ≈ 261.67 cm³
Total Surface Area: A = 3 × π × r² = 3 × 3.14 × (5 × 5) = 3 × 3.14 × 25 ≈ 235.5 cm²
Real-World Connection
The Earth is divided into the Northern Hemisphere and Southern Hemisphere by the equator, and into Eastern and Western Hemispheres by the Prime Meridian.
Practice Quiz
Test your knowledge about hemispheres with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about hemispheres:
Geometry Trivia
Discover interesting facts about hemispheres and geometry:
Ancient Domes
The Pantheon in Rome, built around 126 AD, has a massive hemisphere-shaped dome that remains the world's largest unreinforced concrete dome even today.
Brain Hemispheres
Your brain is divided into two hemispheres - left and right. While they work together, each hemisphere specializes in different functions like language, spatial awareness, and creativity.
Earth's Hemispheres
Our planet is divided into Northern and Southern Hemispheres by the equator, and Eastern and Western Hemispheres by the Prime Meridian. About 90% of the world's population lives in the Northern Hemisphere.
Mathematical Constant
The ratio of a hemisphere's volume to a cylinder with the same radius and height is 2:3. This was discovered by Archimedes, who was so proud of this discovery that he requested it be engraved on his tombstone.





