Intercept Form - Definition, Examples, Quiz, FAQ, Trivia
Learn about x-intercepts and y-intercepts with easy explanations, visual examples, and practice activities
What is Intercept Form?
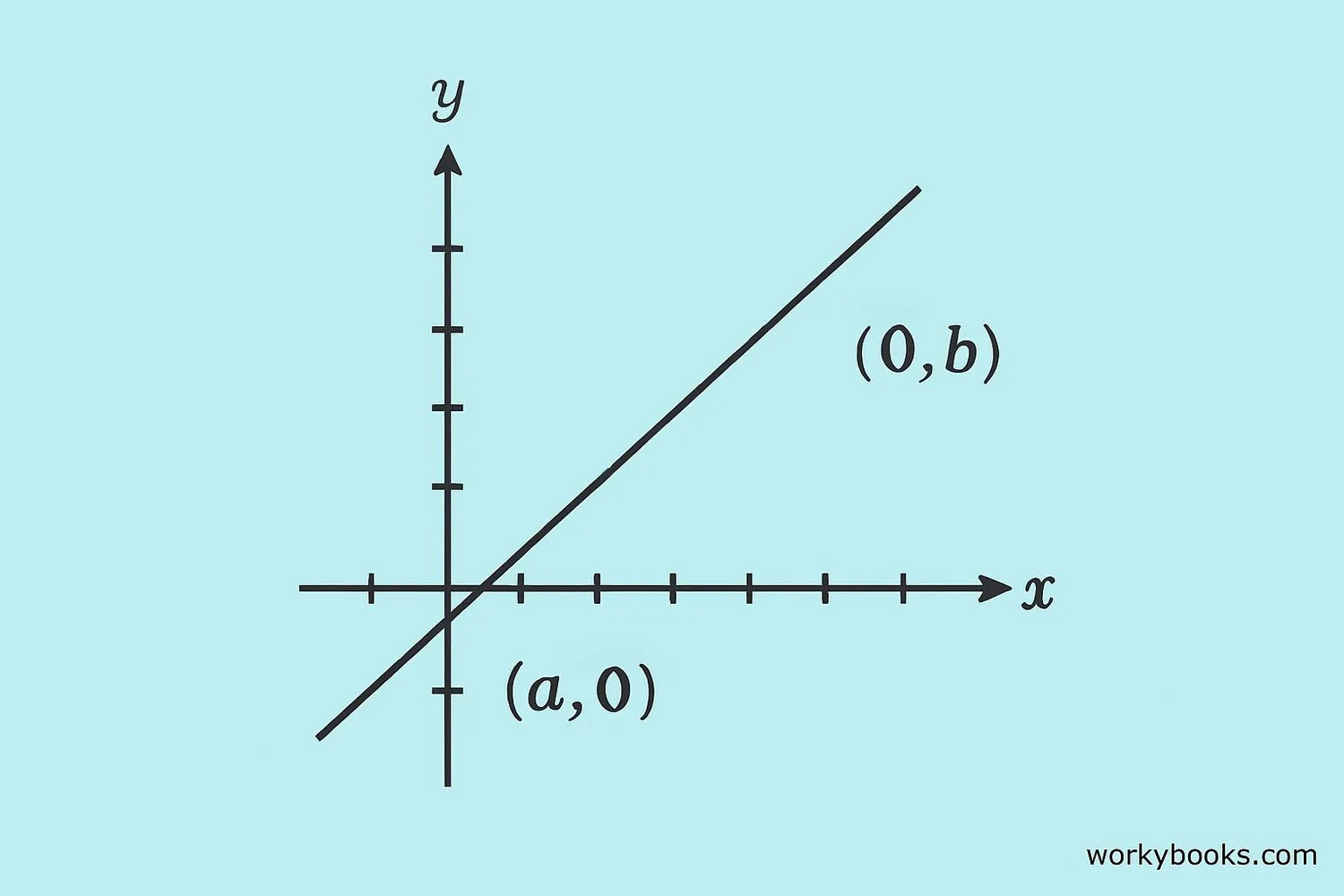
The intercept form is a way to write the equation of a line based on where it crosses the x-axis and y-axis. These crossing points are called intercepts.
The x-intercept is where the line crosses the x-axis. At this point, the y-value is always 0. The y-intercept is where the line crosses the y-axis. At this point, the x-value is always 0.
The intercept form of a line is written as:
Intercept Form Equation
Where 'a' is the x-intercept and 'b' is the y-intercept.
Key Concept
Intercepts are points where a line crosses the axes. The x-intercept is (a, 0) and the y-intercept is (0, b).
How to Find Intercepts
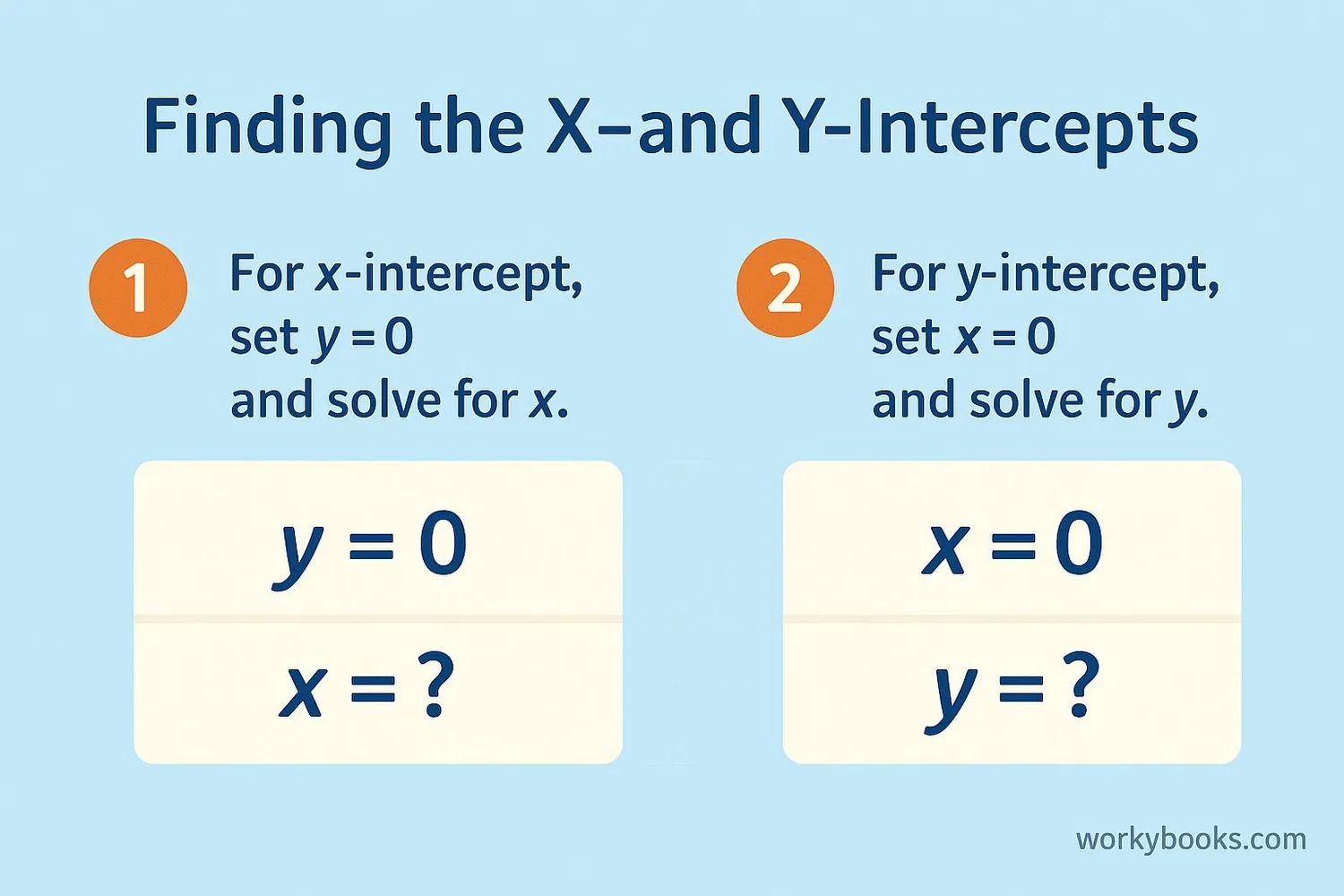
Finding intercepts from an equation is straightforward when you follow these steps:
To find the x-intercept:
Set y = 0 in the equation and solve for x.
To find the y-intercept:
Set x = 0 in the equation and solve for y.
Let's try an example with the equation: 2x + 3y = 6
Finding x-intercept:
Set y = 0: 2x + 3(0) = 6 → 2x = 6 → x = 3
So the x-intercept is (3, 0)
Finding y-intercept:
Set x = 0: 2(0) + 3y = 6 → 3y = 6 → y = 2
So the y-intercept is (0, 2)
Remember
When finding intercepts, always set the other variable to zero. For x-intercept, set y=0. For y-intercept, set x=0.
Graphing Lines Using Intercept Form
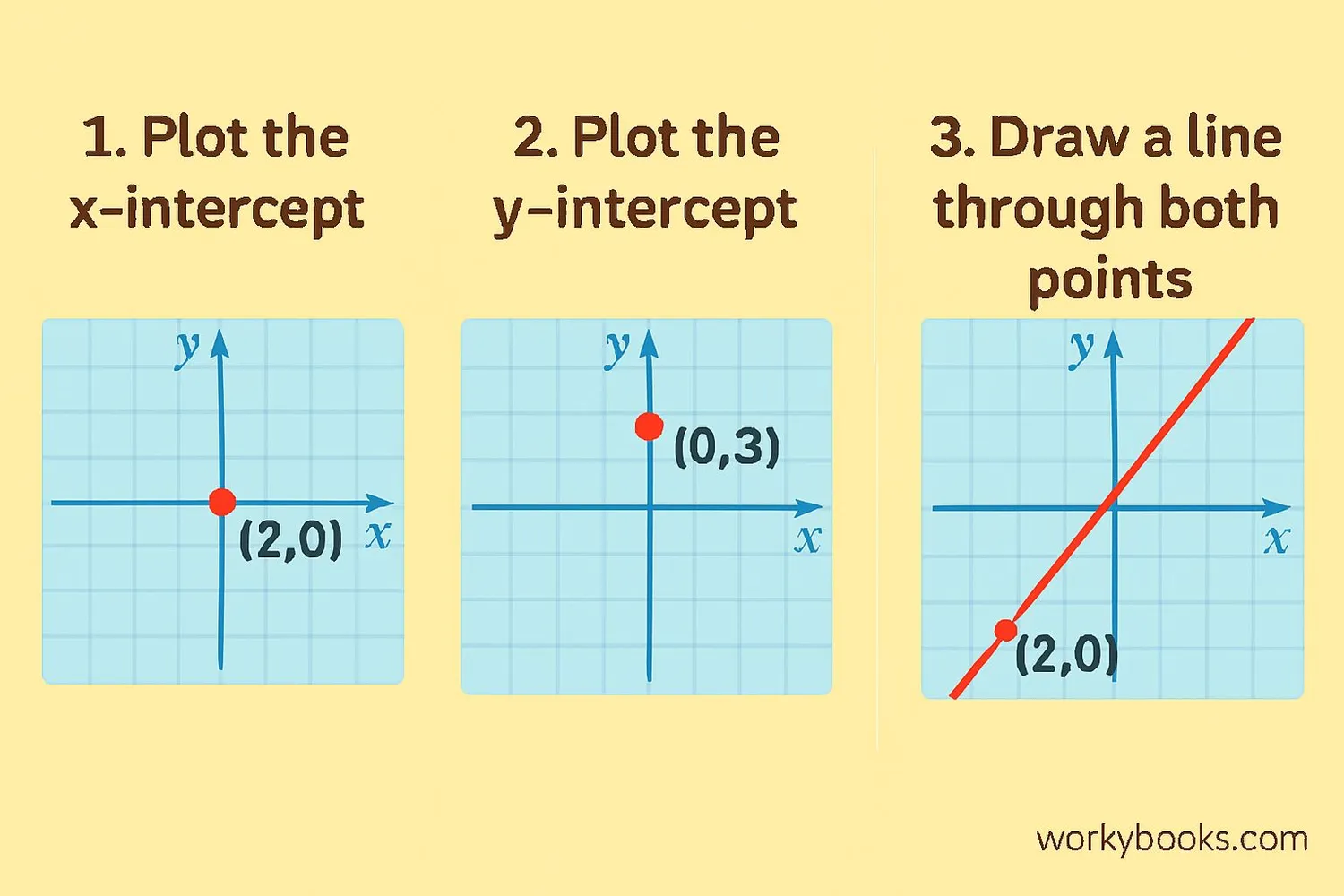
Graphing a line using intercepts is one of the easiest methods. Here's how to do it:
Step 1: Find the x-intercept by setting y=0 and solving for x
Step 2: Find the y-intercept by setting x=0 and solving for y
Step 3: Plot both intercept points on the coordinate plane
Step 4: Draw a straight line through both points
Let's graph the line: 4x + 2y = 8
Find x-intercept: Set y=0 → 4x = 8 → x=2 → (2, 0)
Find y-intercept: Set x=0 → 2y = 8 → y=4 → (0, 4)
Now plot the points (2, 0) and (0, 4) on the graph, then draw a line through them.
Graphing Tip
Always find a third point to check your line. For example, if x=1, then 4(1) + 2y = 8 → 2y = 4 → y=2. The point (1, 2) should also be on your line.
Real-World Examples

Intercepts are used in many real-world situations. Let's explore some examples:
Example 1: Budget Planning
You have $100 to spend on books ($10 each) and pens ($2 each). The equation is: 10x + 2y = 100
x-intercept: (10, 0) → If you buy only books, you can get 10 books
y-intercept: (0, 50) → If you buy only pens, you can get 50 pens
Example 2: Sports Field
A soccer field is marked with boundary lines. The center line can be represented by the equation: x/50 + y/30 = 1
This means the line crosses the x-axis at (50, 0) and the y-axis at (0, 30)
Example 3: Business Profit
A company's profit can be modeled by: P = -2x + 100
x-intercept: (50, 0) → The company breaks even after selling 50 items
y-intercept: (0, 100) → The company has $100 profit before selling any items (starting capital)
Real-World Connection
Intercepts often represent limits or starting points in real situations. The x-intercept might show when something runs out, and the y-intercept might show a starting value.
Intercept Form Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about intercept form:
Math Trivia
Discover interesting facts about coordinate geometry and intercepts:
Cartesian Coordinates
The coordinate system we use today is called the Cartesian coordinate system, named after French mathematician René Descartes. He developed this system in the 17th century.
Real-World Applications
Intercepts are used in many fields beyond mathematics. Economists use them to find break-even points, physicists use them to determine equilibrium, and engineers use them for design limitations.
Special Lines
Lines that pass through the origin (0,0) have both intercepts at the same point. This means their x-intercept and y-intercept are both (0,0).
Global Language
Mathematics is often called the universal language. The concepts of intercepts and coordinate systems are understood the same way by mathematicians all around the world.





