Lowest Terms - Definition, Examples, Quiz, FAQ, Trivia
Learn to simplify fractions to their simplest form with easy explanations and practice activities
What are Lowest Terms?
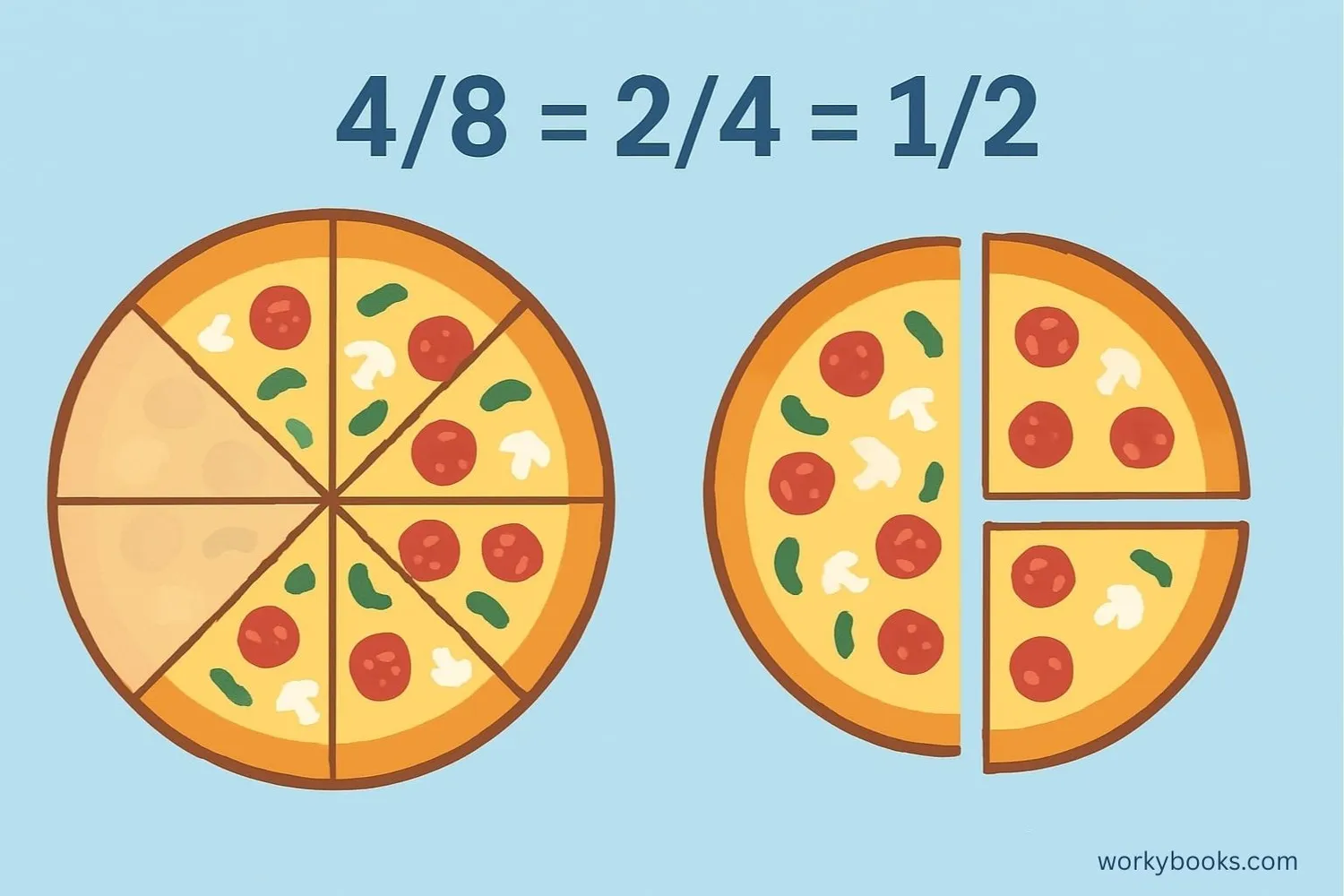
A fraction is in its lowest terms (or simplest form) when the numerator and denominator have no common factors other than 1. This means the fraction cannot be simplified any further.
Think of it like reducing a fraction to its most basic form. For example, the fraction 4/8 can be simplified to 2/4, and then to 1/2. The fraction 1/2 is in its lowest terms because 1 and 2 have no common factors other than 1.
Simplifying fractions makes them easier to understand, compare, and work with in math problems. It's like cleaning up your room so you can find things more easily!
Key Concept
A fraction is in lowest terms when the numerator and denominator have no common factors other than 1.
How to Simplify Fractions to Lowest Terms
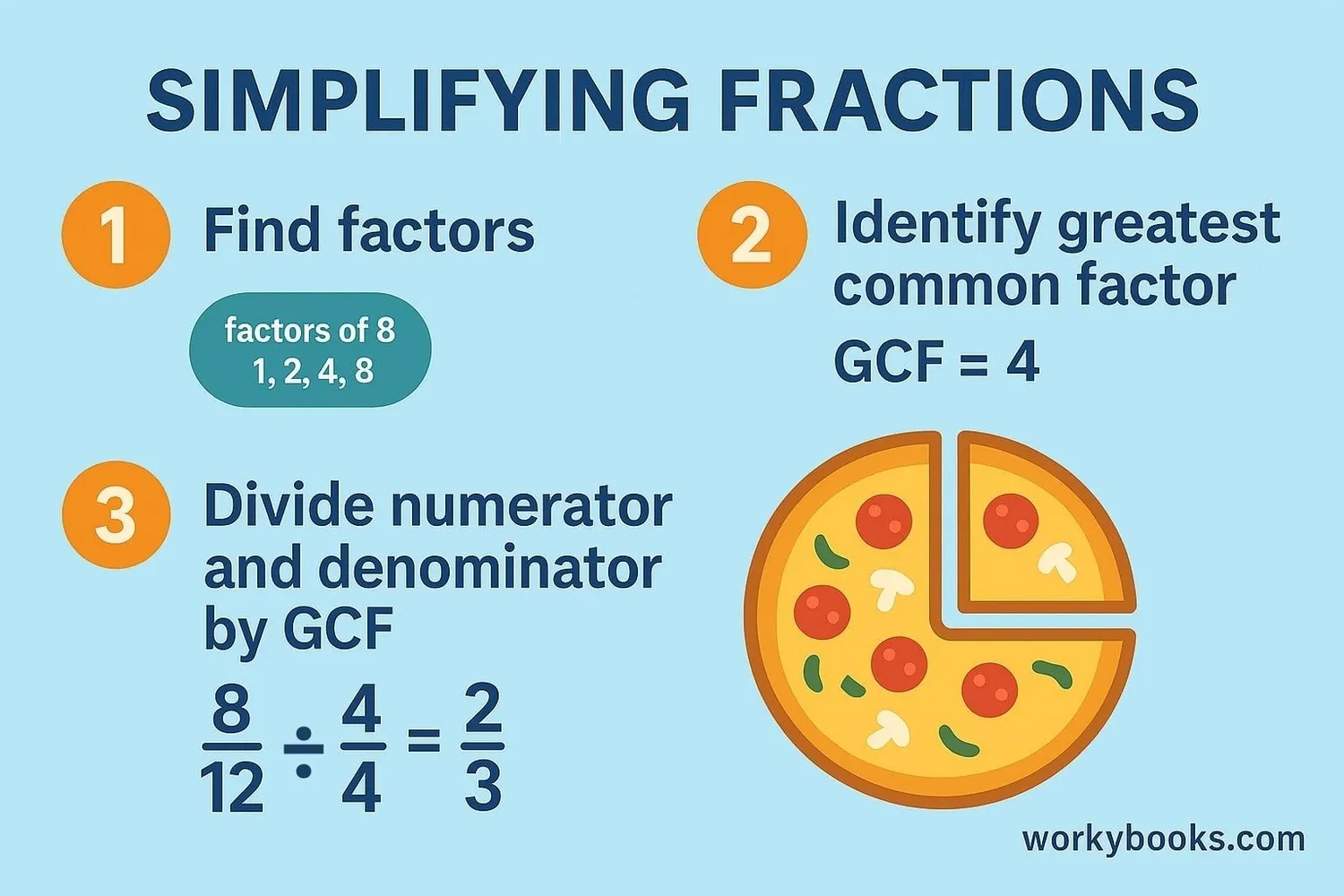
Simplifying fractions to their lowest terms is a simple process when you follow these steps:
Simplification Formula
Divide both the numerator and denominator by their greatest common factor.
Let's practice with an example:
Example: Simplify 8/12 to its lowest terms
Step 1: Factors of 8 are 1, 2, 4, 8. Factors of 12 are 1, 2, 3, 4, 6, 12.
Step 2: The greatest common factor is 4.
Step 3: Divide both numerator and denominator by 4: 8 ÷ 4 = 2, 12 ÷ 4 = 3.
Step 4: The simplified fraction is 2/3.
So 8/12 in lowest terms is 2/3.
Remember
Always check if your simplified fraction can be reduced further. If the numerator and denominator still have common factors, continue simplifying.
Examples of Simplifying Fractions

Let's look at more examples of simplifying fractions to their lowest terms:
Example 1: Simplify 6/9
Factors of 6: 1, 2, 3, 6
Factors of 9: 1, 3, 9
Greatest Common Factor: 3
6 ÷ 3 = 2, 9 ÷ 3 = 3
6/9 simplified is 2/3
Example 2: Simplify 15/25
Factors of 15: 1, 3, 5, 15
Factors of 25: 1, 5, 25
Greatest Common Factor: 5
15 ÷ 5 = 3, 25 ÷ 5 = 5
15/25 simplified is 3/5
Example 3: Simplify 18/24
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Greatest Common Factor: 6
18 ÷ 6 = 3, 24 ÷ 6 = 4
18/24 simplified is 3/4
Example 4: Simplify 7/14
Factors of 7: 1, 7
Factors of 14: 1, 2, 7, 14
Greatest Common Factor: 7
7 ÷ 7 = 1, 14 ÷ 7 = 2
7/14 simplified is 1/2
Practice Tip
Some fractions are already in their simplest form, like 3/5 or 2/7. If the numerator and denominator have no common factors other than 1, the fraction is already simplified.
Simplification Practice Quiz
Test your fraction simplification skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about fractions and lowest terms:
Math Trivia
Discover interesting facts about fractions and mathematics:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they mainly used unit fractions (fractions with 1 as the numerator). They would write other fractions as sums of unit fractions.
Fraction Word Origin
The word "fraction" comes from the Latin word "fractus" which means "broken." This makes sense because fractions represent parts of a whole - like a broken piece of something!
Common Denominator
The method of finding a common denominator to work with fractions was developed by Greek mathematicians over 2,000 years ago. This shows that people have been working with fractions for a very long time!
Golden Ratio
The golden ratio (approximately 1.618) is a special number that appears in nature, art, and architecture. It can be expressed as a continued fraction that goes on forever without repeating.





