Mathematical Formulas - Definition, Examples, Quiz, FAQ, Trivia
Learn about formulas with easy explanations, examples, and interactive activities
What is a Formula?
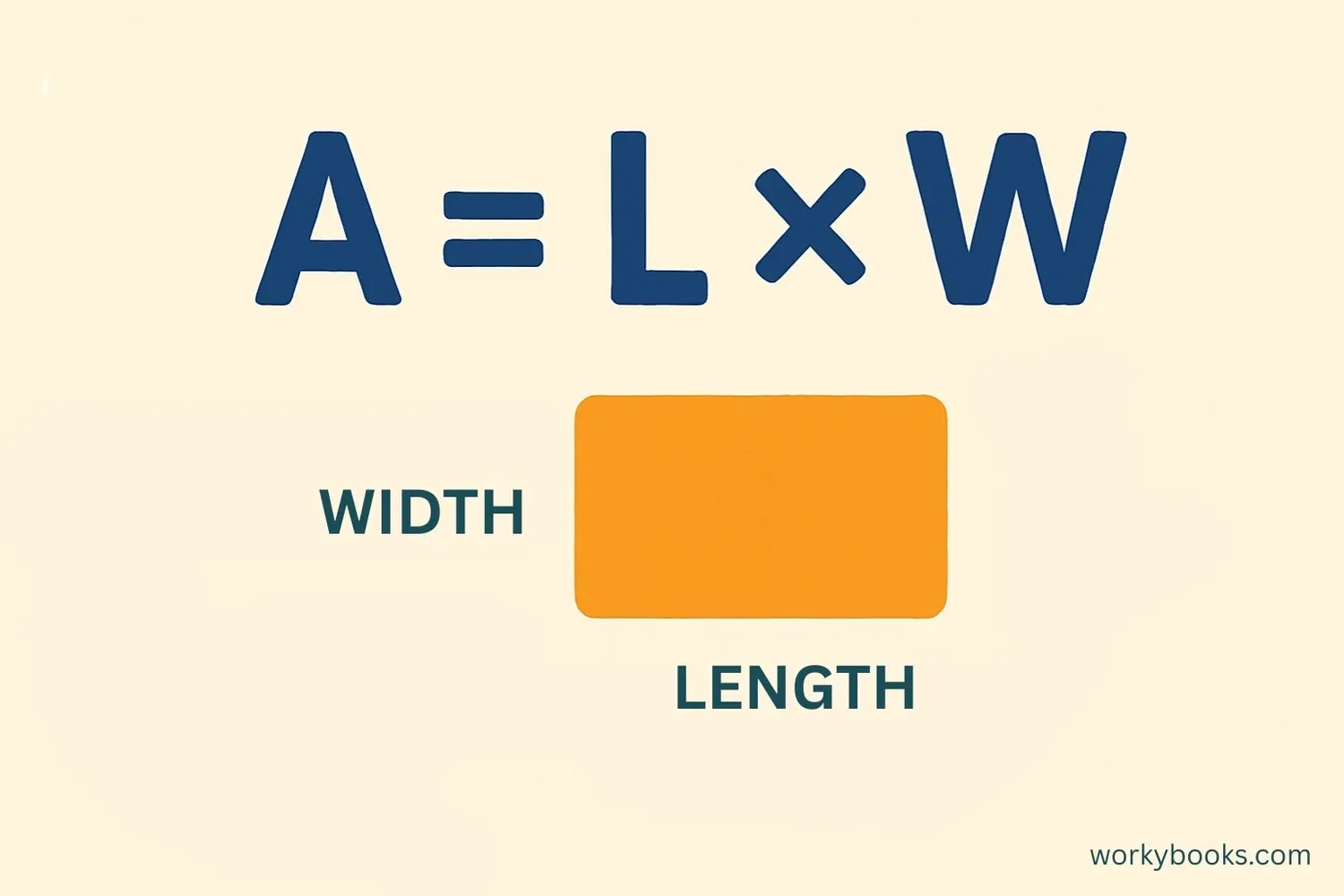
A formula is a special mathematical rule that uses symbols and numbers to show a relationship between different quantities. Think of it as a recipe that tells you how to solve a math problem step by step.
Formulas are like shortcuts that help us solve problems quickly without having to figure everything out from scratch each time. They're used in many areas of math, including geometry, algebra, and measurement.
For example, the formula for finding the area of a rectangle is: Area = Length × Width. This tells us that if we know the length and width of a rectangle, we can multiply them to find the area.
Key Concept
A formula is a mathematical rule that uses symbols to show relationships between different quantities.
Types of Formulas
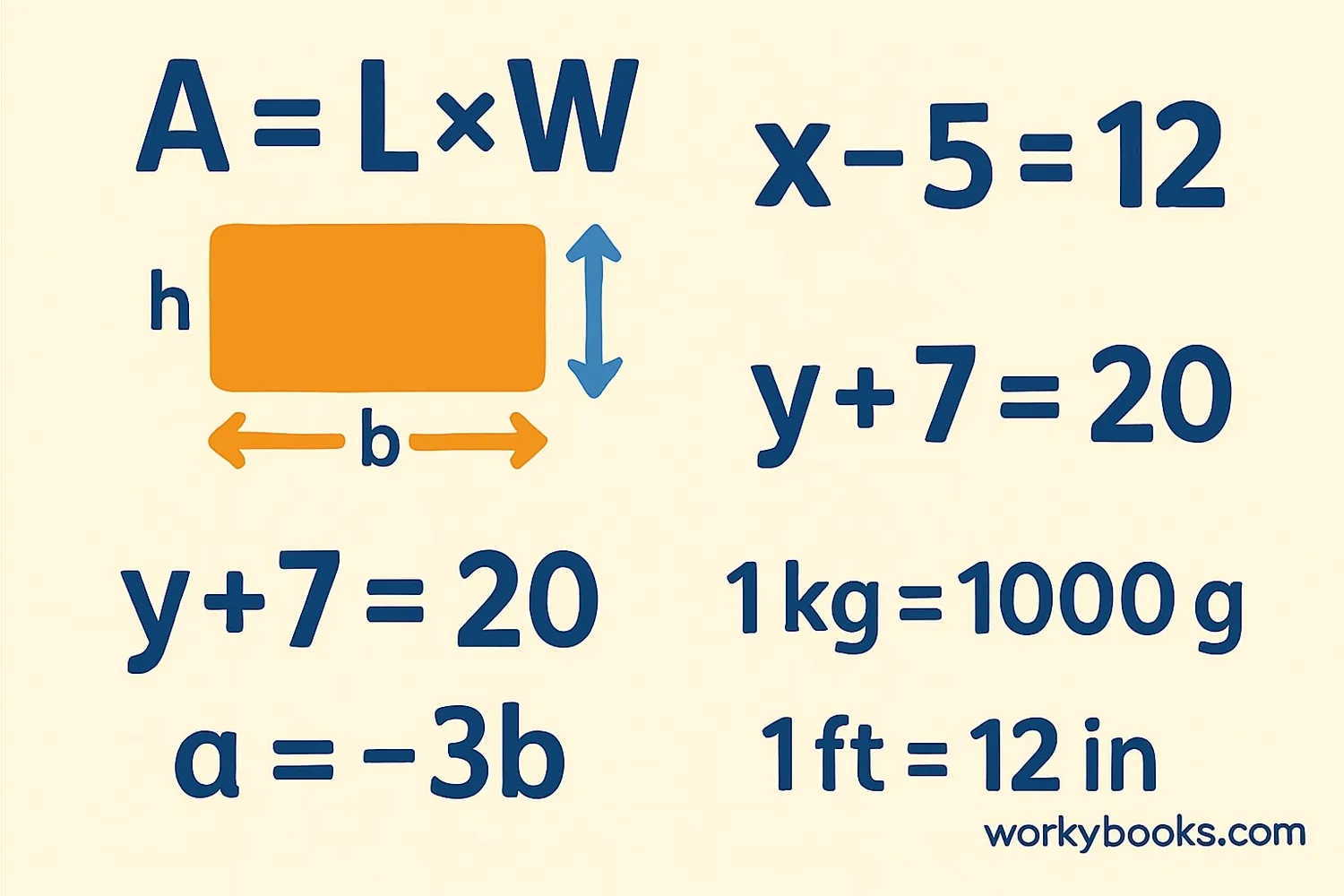
There are many different types of formulas used in mathematics. Here are some common ones you might learn about:
Geometry Formulas
| Shape | Perimeter Formula | Area Formula |
|---|---|---|
| Rectangle | P = 2(L + W) | A = L × W |
| Square | P = 4 × S | A = S × S |
| Triangle | P = a + b + c | A = ½ × b × h |
| Circle | C = 2πr | A = πr² |
Measurement Formulas
| Measurement | Formula |
|---|---|
| Volume of a rectangular prism | V = L × W × H |
| Temperature conversion (Fahrenheit to Celsius) | °C = (°F - 32) × 5/9 |
| Speed | Speed = Distance ÷ Time |
| Arithmetic mean (average) | Average = Sum ÷ Count |
Remember
Different formulas help us solve different types of problems. It's important to choose the right formula for each situation.
Formula Examples
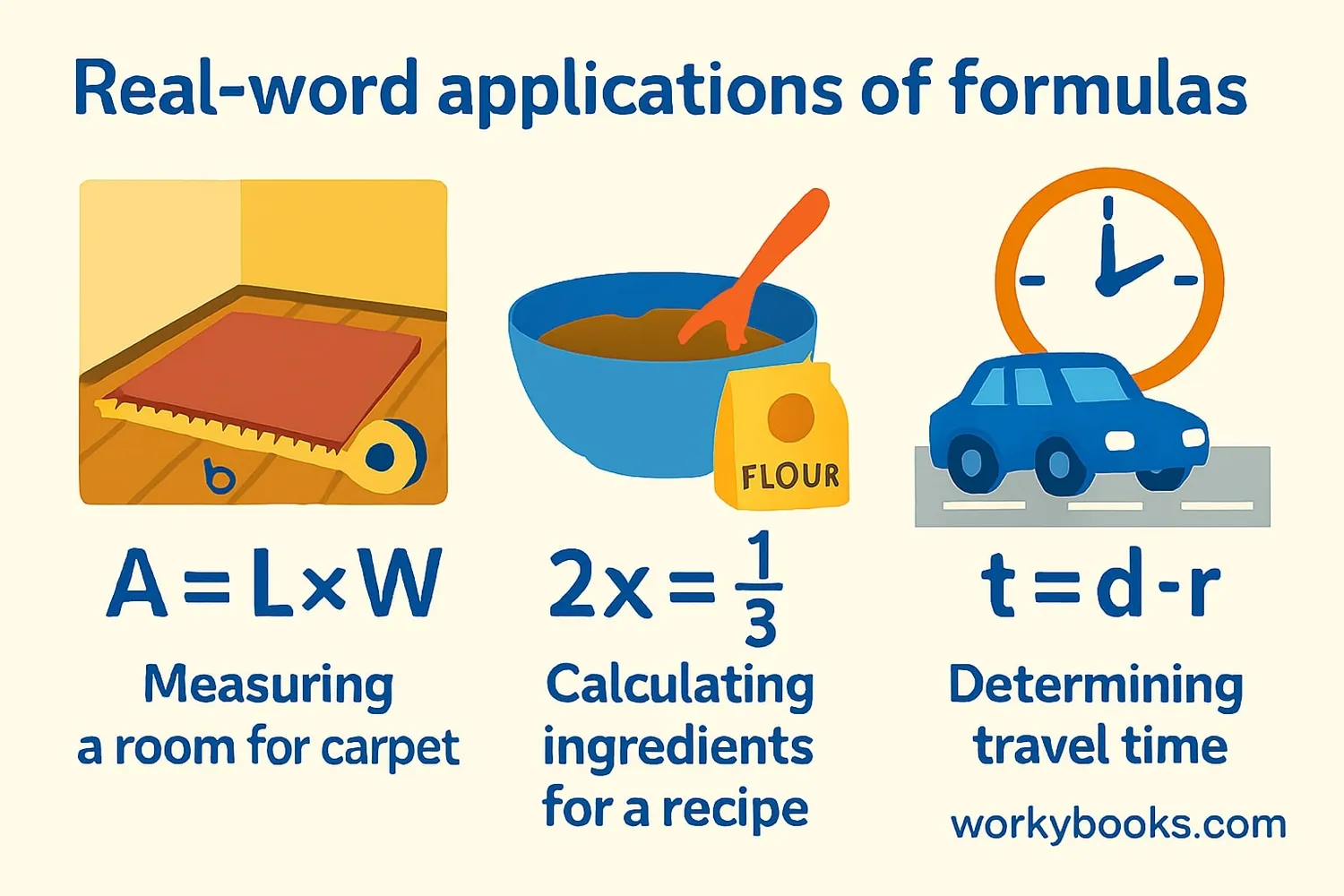
Let's look at some examples of how formulas work in real situations:
Example 1: Finding the area of a rectangular garden that is 5 meters long and 3 meters wide.
Formula: Area = Length × Width
Solution: 5 m × 3 m = 15 square meters
Example 2: Calculating the perimeter of a square playground with sides of 8 meters each.
Formula: Perimeter = 4 × Side
Solution: 4 × 8 m = 32 meters
Example 3: Finding the volume of a box that is 4 cm long, 3 cm wide, and 2 cm high.
Formula: Volume = Length × Width × Height
Solution: 4 cm × 3 cm × 2 cm = 24 cubic centimeters
Example 4: Converting 68° Fahrenheit to Celsius.
Formula: °C = (°F - 32) × 5/9
Solution: (68 - 32) × 5/9 = 36 × 5/9 = 20°C
Pythagorean Theorem
This famous formula helps find the length of sides in right triangles.
Practice Tip
Try using formulas to solve problems you encounter in daily life, like measuring your room or calculating how long a trip will take.
Formula Practice Quiz
Test your understanding of formulas with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about mathematical formulas:
Math Trivia
Discover interesting facts about mathematical formulas:
Ancient Formulas
The ancient Babylonians knew about the Pythagorean theorem (a² + b² = c²) over 1,000 years before Pythagoras was born! They used it for surveying land and building structures.
Euler's Formula
Mathematician Leonhard Euler discovered a special formula: e^(iπ) + 1 = 0. It's called the most beautiful formula in mathematics because it connects five important mathematical constants.
Rocket Science
The Tsiolkovsky rocket equation is a formula that describes how rockets work. It helped scientists calculate how to send astronauts to the moon and satellites into space.
Longest Proof
The longest mathematical proof ever created is a file that is 200 terabytes in size! That's about the size of all the text in the entire Wikipedia history.





