Median of a Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn about triangle medians with easy explanations, visual examples, and practice activities
What is a Median of a Triangle?
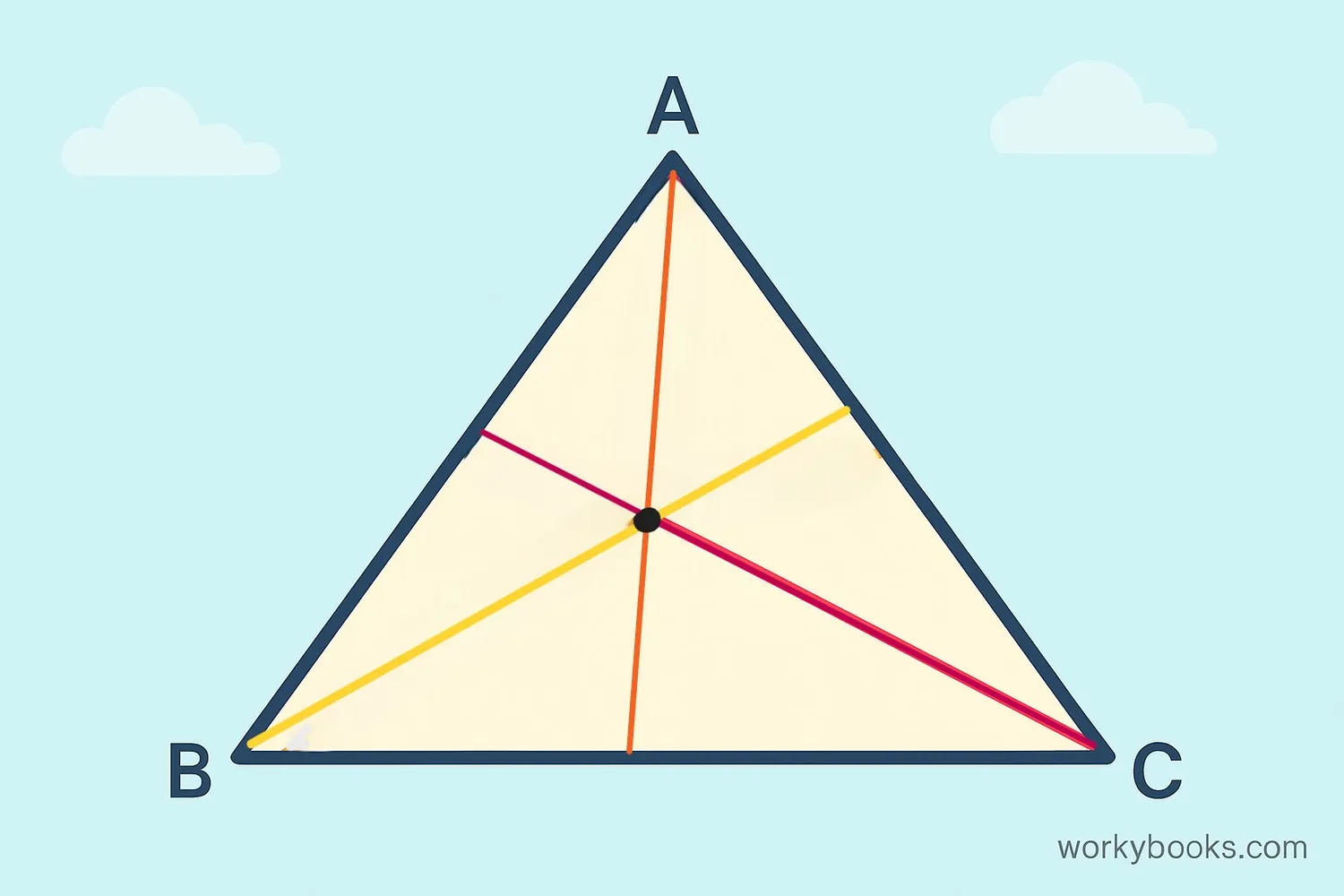
A median of a triangle is a special line segment that connects a vertex (corner) of the triangle to the midpoint of the opposite side. Every triangle has three medians, one from each vertex.
Think of it like this: if you want to divide a side of a triangle into two equal parts, you would find its midpoint. Then if you draw a line from the opposite vertex to that midpoint, you've drawn a median!
The point where all three medians meet is called the centroid. This special point is always inside the triangle and is the center of gravity of the triangle.
Key Concept
A median connects a vertex to the midpoint of the opposite side. Every triangle has exactly three medians.
Properties of Medians
Medians have some interesting properties that make them special:
- All three medians always intersect at a single point called the centroid, no matter what shape the triangle is.
- The centroid divides each median in a 2:1 ratio. This means the distance from the vertex to the centroid is twice the distance from the centroid to the midpoint of the side.
- The three medians divide the triangle into six smaller triangles that all have exactly the same area.
- The centroid is the center of gravity of the triangle. If you could balance the triangle on a pencil point, it would balance perfectly at the centroid.
Remember
Every triangle has exactly three medians, and they always intersect at the centroid, which is the center of gravity of the triangle.
How to Draw a Median
Drawing a median is easy! Here's how you can do it:
Step 1: Identify which vertex you want to start from and which side is opposite to it.
Step 2: Find the midpoint of the opposite side. You can measure the side and mark its exact middle point.
Step 3: Use a ruler to draw a straight line from the vertex to the midpoint you found.
That's it! You've drawn a median. To find all three medians, repeat these steps for each vertex.
When you draw all three medians, you'll notice they all meet at exactly the same point - the centroid!
Important Ratio
The centroid divides each median so that the section from the vertex is twice as long as the section to the midpoint.
Examples of Medians
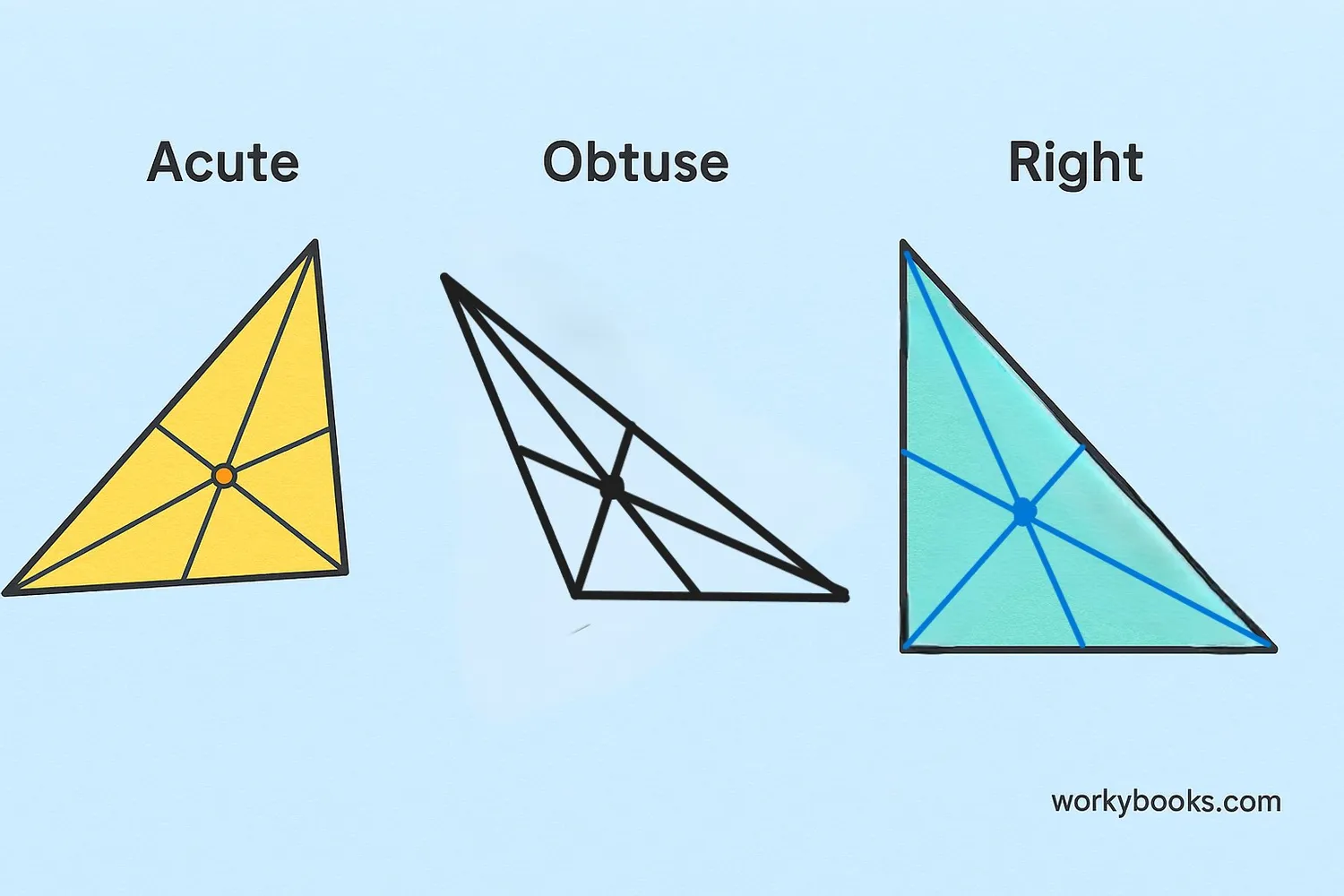
Let's look at some examples of medians in different types of triangles:
Example 1: In an equilateral triangle (all sides equal), all three medians are the same length. The centroid is exactly at the center.
Example 2: In an isosceles triangle (two sides equal), two medians are equal in length, and the third is different.
Example 3: In a scalene triangle (all sides different), all three medians have different lengths.
Example 4: No matter what type of triangle you have - acute, right, or obtuse - the three medians will always intersect at the centroid, and this point is always inside the triangle.
Try drawing different triangles and constructing their medians. You'll discover that these properties always hold true!
Try This
Draw a triangle on paper, find the midpoints of each side, and draw the medians. See if they all meet at one point!
Median of a Triangle Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about medians of triangles:
Geometry Trivia
Discover interesting facts about triangles and geometry:
Ancient Geometry
The study of triangle centers like the centroid dates back to ancient Greek mathematicians. Euclid described the centroid in his famous work "Elements" around 300 BCE.
Center of Gravity
Engineers use the centroid concept when designing structures. The center of gravity helps determine how weight is distributed and how structures will behave under force.
In the Real World
Artists sometimes use the centroid when composing drawings or paintings. Placing important elements near the centroid can create a balanced and pleasing composition.
Coordinate Geometry
If you know the coordinates of a triangle's vertices, you can calculate the centroid by averaging the x-coordinates and averaging the y-coordinates of the three vertices.





