Negative Exponents - Definition, Examples, Quiz, FAQ, Trivia
Learn to work with negative exponents using simple rules and practice activities
What Are Negative Exponents?
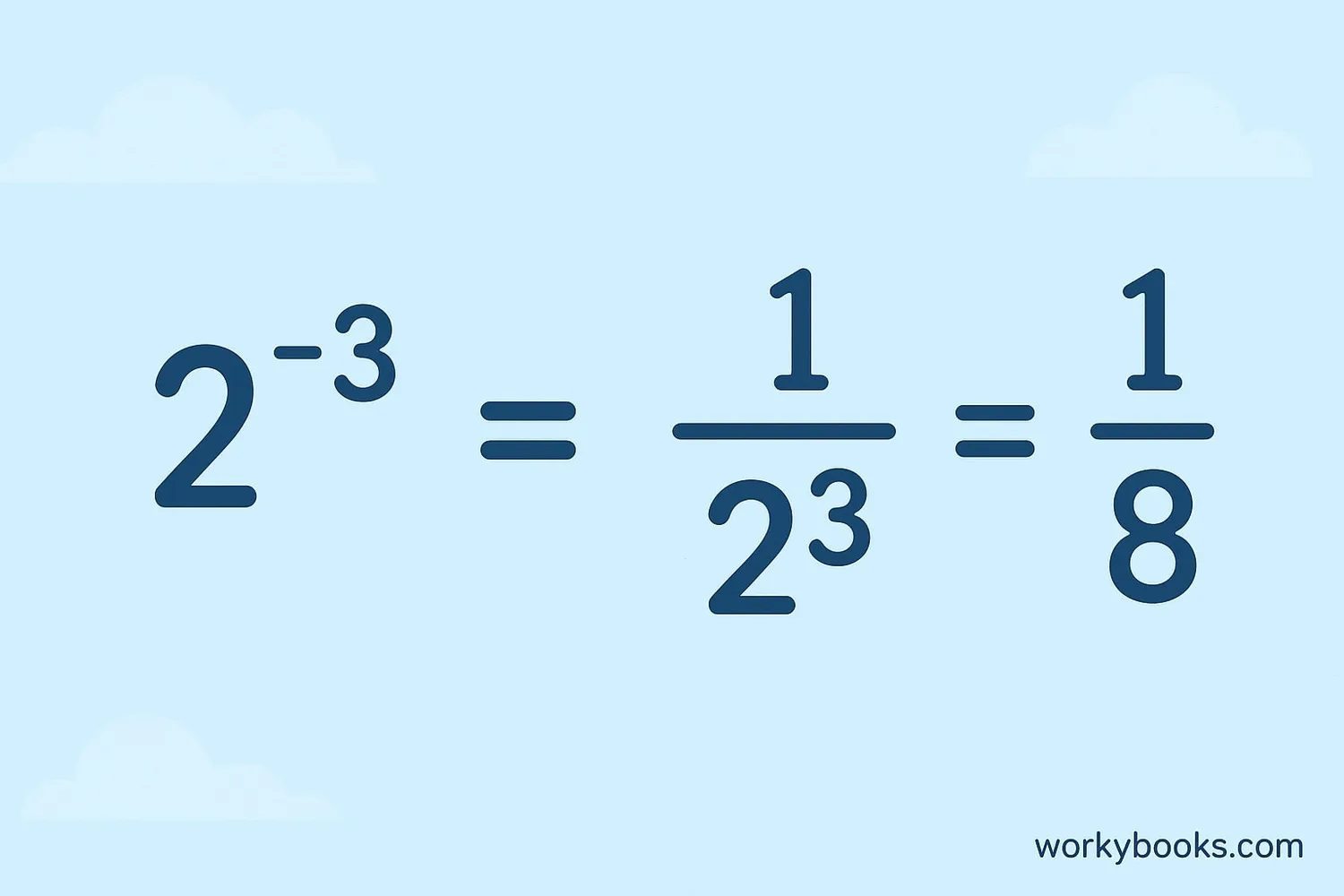
Negative exponents might seem confusing at first, but they have a simple meaning. A negative exponent tells us to take the reciprocal of the base raised to the positive exponent.
Definition: For any non-zero number a and positive integer n,
a⁻ⁿ = 1/aⁿ
This means that a negative exponent "flips" the base to the denominator. For example:
5⁻² = 1/5² = 1/25
3⁻³ = 1/3³ = 1/27
Why do we need negative exponents? They help us write very small numbers in a compact way and follow consistent mathematical rules.
Key Concept
This relationship is the foundation for working with negative exponents.
Negative Exponent Rules
There are several important rules that make working with negative exponents easier. These rules help us simplify expressions and solve problems:
Reciprocal Rule
a⁻ⁿ = 1/aⁿ and 1/a⁻ⁿ = aⁿ
Example: 4⁻² = 1/4² = 1/16
Fraction Rule
(a/b)⁻ⁿ = (b/a)ⁿ
Example: (2/3)⁻² = (3/2)² = 9/4
Multiplying Rule
a⁻ᵐ × a⁻ⁿ = a⁻⁽ᵐ⁺ⁿ⁾
Example: 5⁻³ × 5⁻² = 5⁻⁵ = 1/3125
Dividing Rule
a⁻ᵐ ÷ a⁻ⁿ = a⁻⁽ᵐ⁻ⁿ⁾
Example: 7⁻⁴ ÷ 7⁻² = 7⁻² = 1/49
Remember
Negative exponents do not make the result negative - they make it a fraction. For example, 3⁻² = 1/9, not -9.
Fractions with Negative Exponents
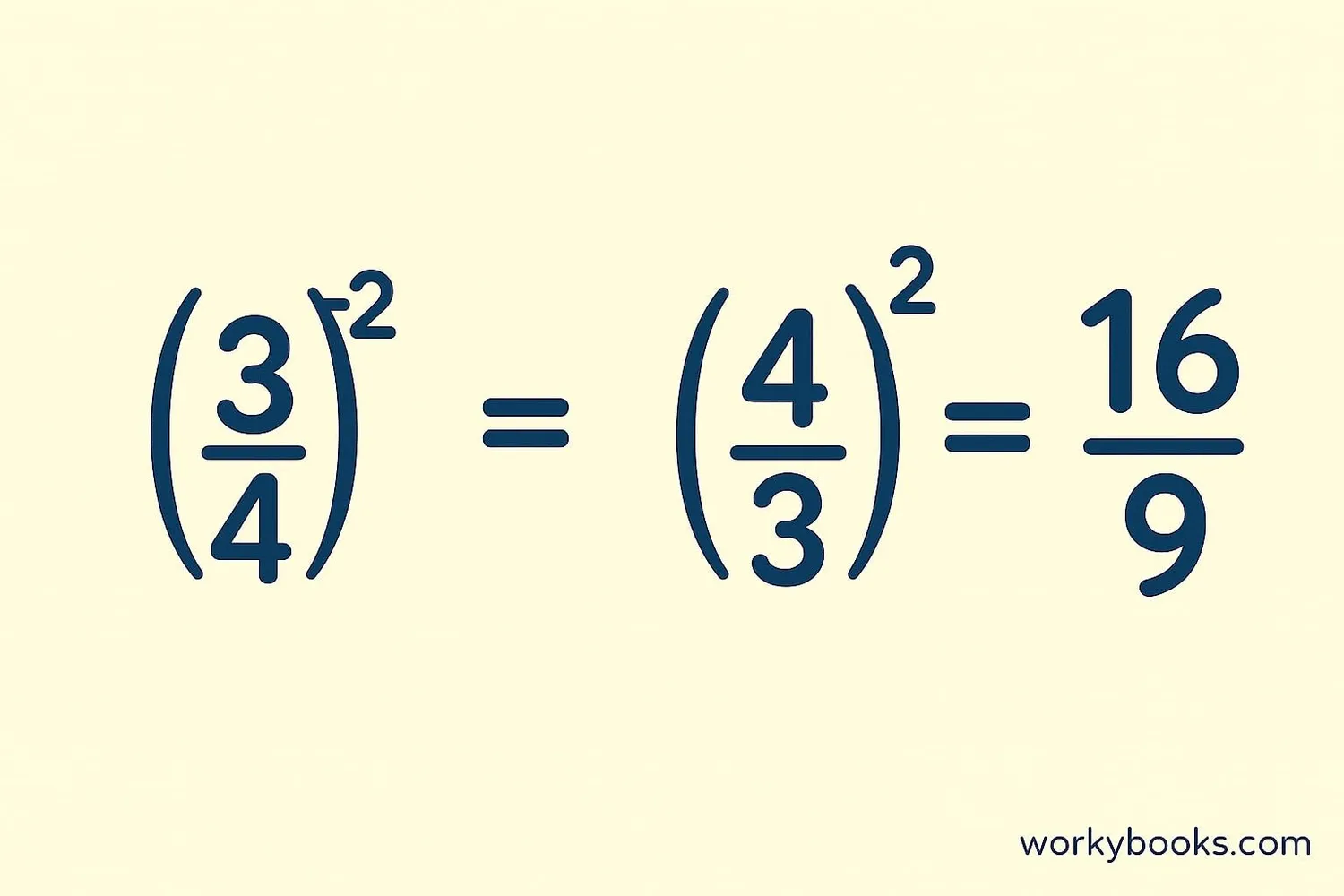
When fractions have negative exponents, we apply the same reciprocal rule but to the entire fraction. The negative exponent flips the fraction.
Rule: (a/b)⁻ⁿ = (b/a)ⁿ
This means we can "flip" the fraction and make the exponent positive. Let's look at some examples:
Example 1
(2/5)⁻² = (5/2)² = 25/4
The negative exponent flips the fraction to 5/2, then we square both numbers.
Example 2
(1/3)⁻³ = (3/1)³ = 27
Flipping 1/3 gives us 3/1, then we cube 3 to get 27.
Example 3
5⁻²/3⁻³ = (3³/5²) = 27/25
Each part with a negative exponent moves to the opposite part of the fraction.
Tip
When you see a negative exponent on a fraction, just flip the fraction and make the exponent positive!
Multiplying Negative Exponents
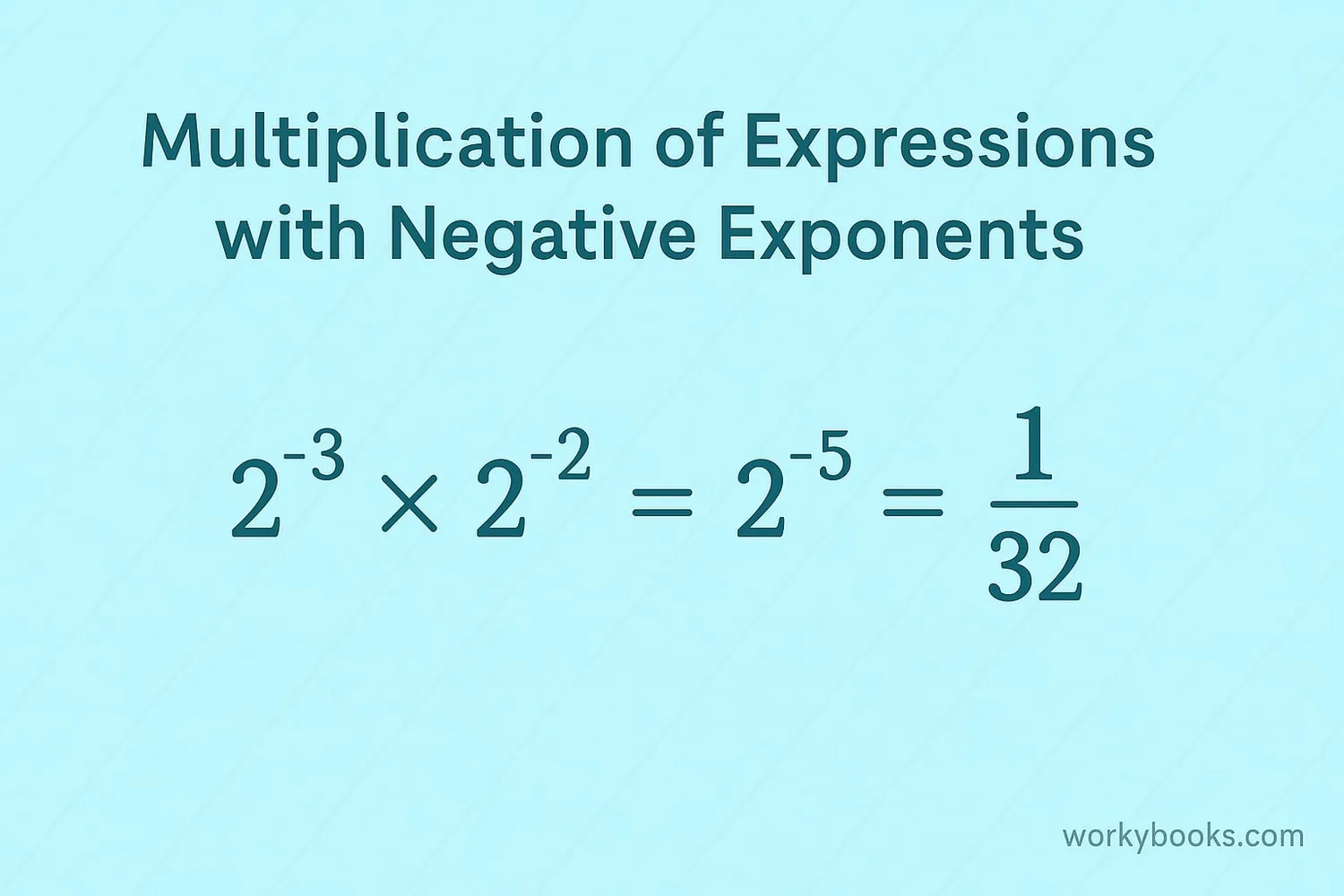
When multiplying expressions with negative exponents, we follow the same rules as with positive exponents. The key is to combine like bases by adding their exponents.
Rule: aᵐ × aⁿ = aᵐ⁺ⁿ
This rule works whether the exponents are positive or negative. Let's look at some examples:
Same Base
4⁻³ × 4⁻² = 4⁻³⁻² = 4⁻⁵ = 1/1024
Add the exponents: -3 + (-2) = -5
Different Bases
5⁻² × 3⁻² = (5×3)⁻² = 15⁻² = 1/225
When bases are different but exponents are the same, multiply the bases first.
Mixed Exponents
2⁻³ × 2⁵ = 2⁻³⁺⁵ = 2² = 4
Combine the exponents: -3 + 5 = 2
Remember
When multiplying expressions with the same base, add the exponents. This works for both positive and negative exponents.
Solving Negative Exponents
Solving problems with negative exponents follows a systematic approach. Here's a step-by-step method:
1. Apply reciprocal rule: Convert negative exponents to positive by taking reciprocals
2. Simplify expressions: Use exponent rules to combine terms
3. Calculate: Perform the arithmetic operations
Let's solve an example together:
Problem: Simplify (3⁻² × 4³) ÷ (3⁻³ × 4⁻¹)
Step 1: Apply reciprocal rule to negative exponents
= (1/3² × 4³) ÷ (1/3³ × 1/4¹)
Step 2: Simplify the expression
= (1/9 × 64) ÷ (1/27 × 1/4)
= (64/9) ÷ (1/(27×4))
= (64/9) ÷ (1/108)
Step 3: Dividing fractions: multiply by reciprocal
= (64/9) × (108/1)
= (64 × 108) / (9 × 1)
Step 4: Simplify
= (64 × 12) (since 108 ÷ 9 = 12)
= 768
Problem Solving Tip
Always convert negative exponents to positive exponents as your first step - it makes the problem much easier to solve!
Negative Exponents Practice Quiz
Test your understanding of negative exponents with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about negative exponents:
Exponent Trivia
Discover interesting facts about exponents and mathematics:
Historical Origins
The concept of exponents dates back to the 3rd century BCE. The Greek mathematician Archimedes used a system similar to exponents when he estimated the number of grains of sand in the universe, which he called "the sand reckoner."
Scientific Applications
Negative exponents are essential in science for representing microscopic measurements. For example, the size of a virus (about 10⁻⁷ meters) and the mass of an electron (9.1 × 10⁻³¹ kg) both use negative exponents.
Calculator Evolution
Early calculators couldn't handle negative exponents directly. Engineers had to use logarithm tables for complex calculations involving negative exponents until electronic calculators became available in the 1970s.
Extremely Small Numbers
The smallest unit of time ever measured is about 10⁻²¹ seconds (one sextillionth of a second). This was achieved by scientists studying particle physics and required the use of negative exponents to express.





