Nth Term - Definition, Examples, Quiz, FAQ, Trivia
Learn to recognize patterns, find rules, and predict sequences with the nth term
What is the nth term?
The nth term is a special rule that tells us any term in a sequence. Think of it like a magic formula that can predict any number in a pattern if you know its position!
In a sequence, each number is called a "term". The position of a term is its "n" value:
- The 1st term: n = 1
- The 2nd term: n = 2
- The 3rd term: n = 3
- ...and so on
The nth term formula lets us find any term without listing all the numbers before it. This is super helpful for finding large terms like the 100th term in a pattern!
Key Concept
The nth term is a formula that lets you calculate any term in a sequence when you know its position (n).
Linear Sequences (Arithmetic)

A linear sequence (also called arithmetic sequence) is one where the difference between consecutive terms is constant. This difference is called the common difference.
To find the nth term formula for a linear sequence:
- Find the common difference (d) between terms
- Multiply the position (n) by the common difference
- Adjust the result to match the first term
Formula for Linear Sequence
Where:
a = first term
d = common difference
n = position
Example Sequence
Common difference (d) = 3
First term (a) = 5
Formula: nth term = 5 + 3×(n-1)
Simplified: nth term = 3n + 2
Find the 10th term
Using formula: nth term = 3×n + 2
For n=10: 3×10 + 2 = 32
So the 10th term is 32
Geometric Sequences
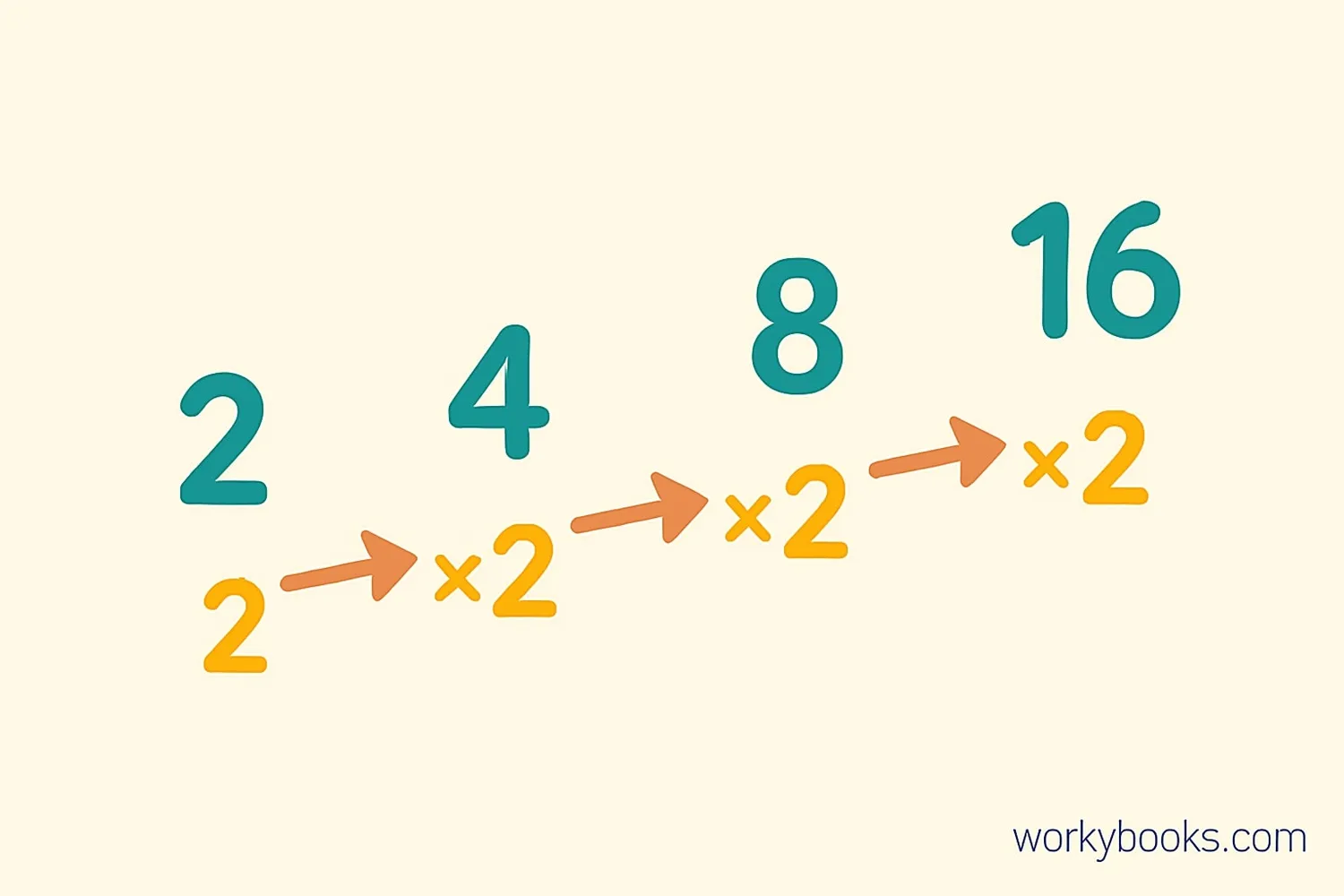
A geometric sequence is one where each term is found by multiplying the previous term by a constant. This constant is called the common ratio.
To find the nth term formula for a geometric sequence:
- Find the common ratio (r) between terms
- Start with the first term (a)
- Multiply by the common ratio raised to (n-1)
Formula for Geometric Sequence
Where:
a = first term
r = common ratio
n = position
Example Sequence
Common ratio (r) = 3
First term (a) = 2
Formula: nth term = 2 × 3(n-1)
Find the 5th term
Using formula: nth term = 2 × 3(5-1)
= 2 × 34
= 2 × 81 = 162
So the 5th term is 162
Real-World Examples
Sequences and the nth term appear in many real-world situations:
Example 1: Theater Seating
The first row has 10 seats, each row adds 3 seats. How many seats in row 15?
Sequence: 10, 13, 16, 19, ...
Common difference (d) = 3
Formula: nth term = 10 + 3×(n-1)
For n=15: 10 + 3×14 = 52 seats
Example 2: Plant Growth
A plant grows to 5cm on day 1, then doubles each day. How tall on day 6?
Sequence: 5, 10, 20, 40, ...
Common ratio (r) = 2
Formula: nth term = 5 × 2(n-1)
For n=6: 5 × 25 = 5 × 32 = 160cm
Example 3: Savings Account
You save $20 each week. How much will you have after 10 weeks?
Sequence: 20, 40, 60, 80, ...
Formula: nth term = 20n
For n=10: 20×10 = $200
Pattern Tip
Look for sequences in everyday life - stair steps, fence posts, or even the pages in a book!
Nth Term Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the nth term:
Math Trivia
Discover interesting facts about sequences and patterns:
Fibonacci Sequence
The Fibonacci sequence (1,1,2,3,5,8,13...) appears throughout nature - in sunflower seeds, pinecones, hurricanes, and even galaxies! Each term is the sum of the two previous terms.
Prime Numbers
There's no known simple formula for the nth prime number. Mathematicians have been trying to find one for centuries! The largest known prime number has over 24 million digits.
Ancient Sequences
The ancient Egyptians used arithmetic sequences over 4000 years ago for accounting and construction. The Rhind Mathematical Papyrus (1650 BCE) contains problems about sequences.
Musical Sequences
Musical scales are based on geometric sequences! The frequency of each note in an octave is multiplied by the same ratio (21/12) to get to the next note.





