Parallelogram - Definition, Examples, Quiz, FAQ, Trivia
Learn about the properties, formulas, and types of parallelograms with examples and activities
What is a Parallelogram?
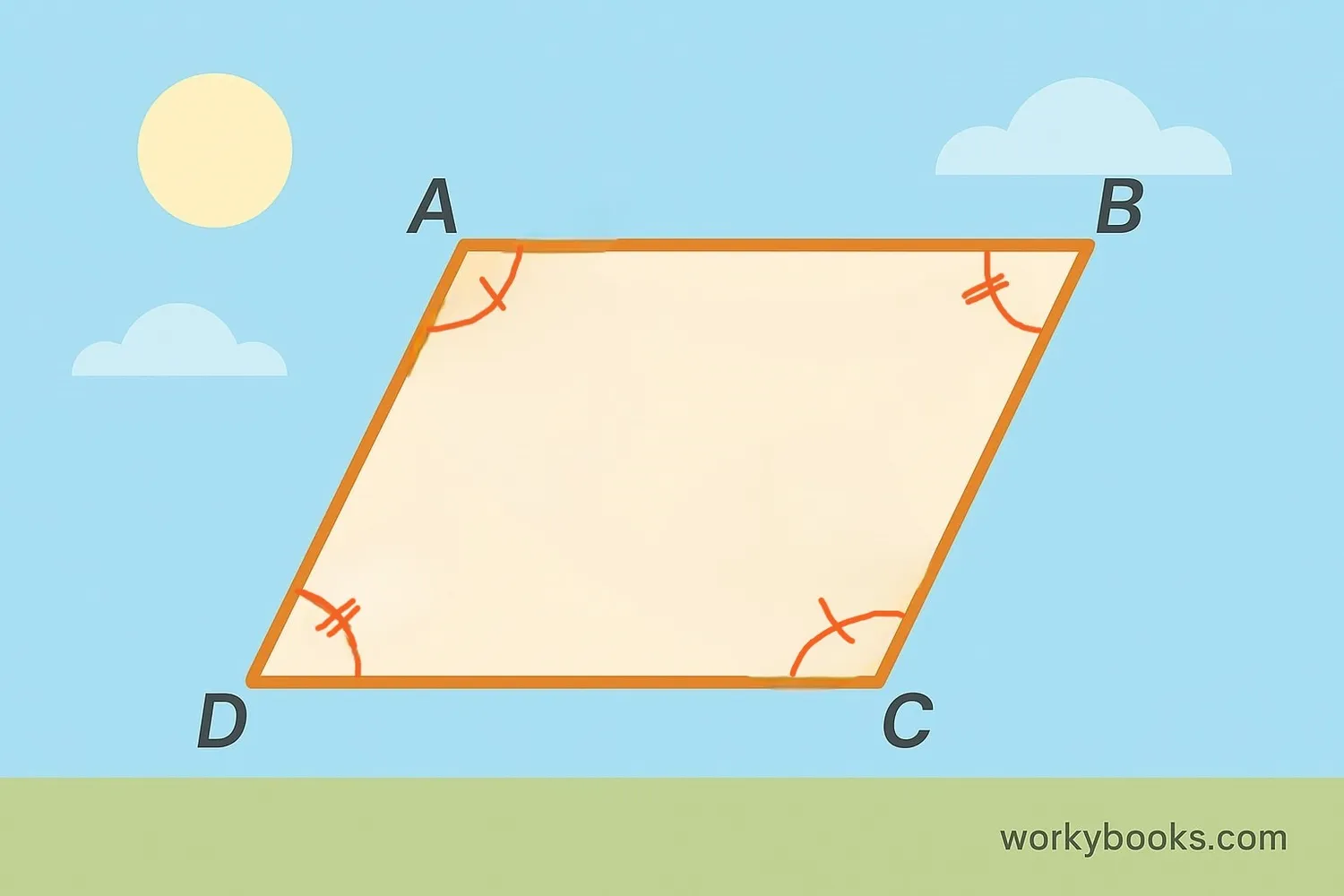
A parallelogram is a special type of quadrilateral (a shape with four sides) where both pairs of opposite sides are parallel and equal in length. This means that side AB is parallel to side CD, and side AD is parallel to side BC. Also, AB = CD and AD = BC.
In simple terms, if you imagine a shape that looks like a slanted rectangle, you're picturing a parallelogram! All rectangles are actually special types of parallelograms with right angles.
Parallelograms are everywhere around us - in tiles, buildings, and even in the design of some bridges. Understanding them helps us solve many real-world problems in math and engineering.
Key Concept
A parallelogram is defined by two main features: opposite sides that are parallel and opposite sides that are equal in length.
Properties of Parallelograms
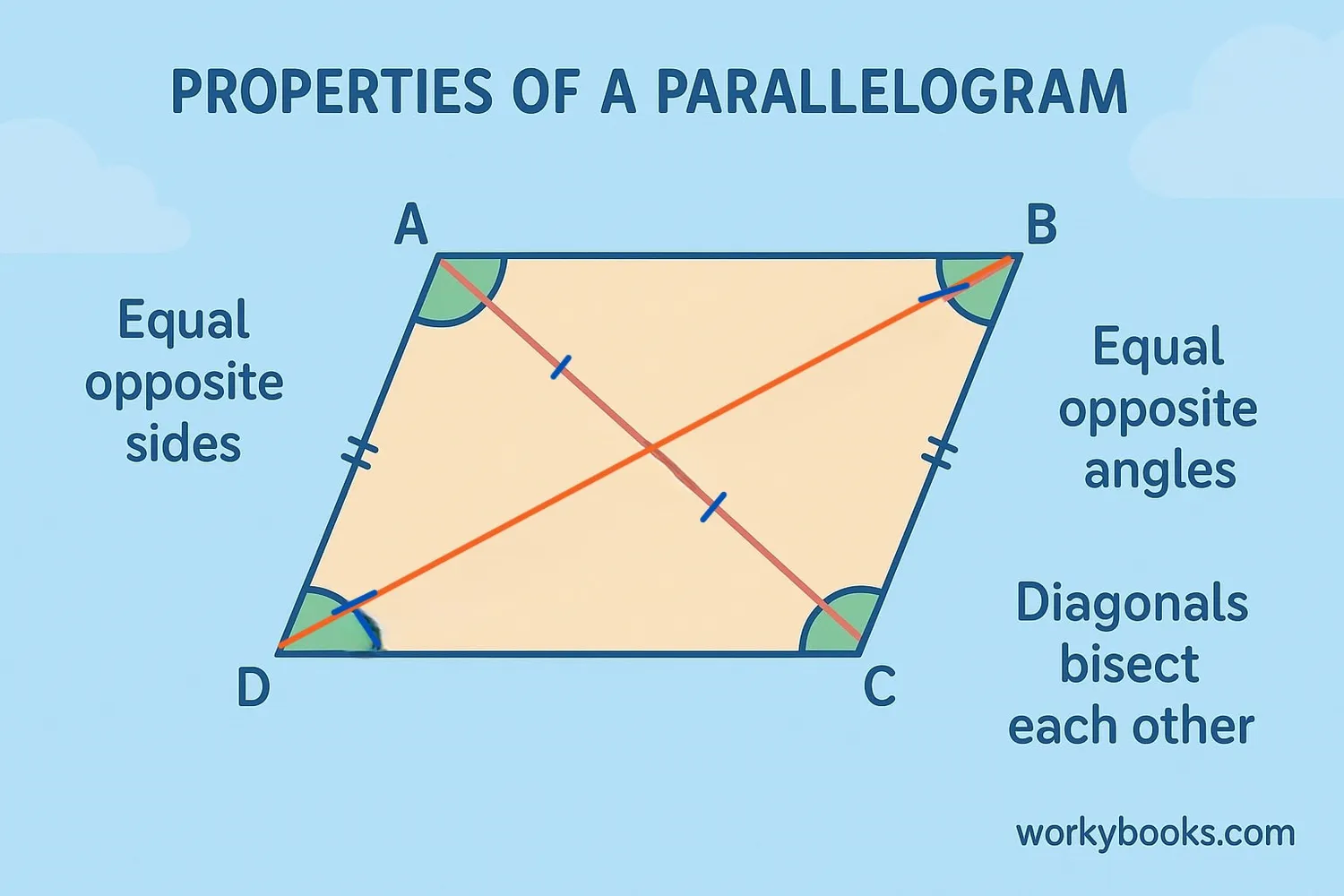
Parallelograms have several special properties that make them unique:
Opposite Sides
Opposite sides of a parallelogram are equal in length. AB = CD and AD = BC.
Opposite Angles
Opposite angles are equal. Angle A = Angle C and Angle B = Angle D.
Consecutive Angles
Consecutive angles (angles next to each other) add up to 180° (they are supplementary).
Diagonals
The diagonals of a parallelogram bisect each other (they cut each other exactly in half).
Remember
If a quadrilateral has just one pair of parallel sides, it's called a trapezoid, not a parallelogram. A parallelogram must have both pairs of opposite sides parallel.
Types of Parallelograms
Rhombus
A parallelogram where all four sides are equal in length. Its diagonals bisect each other at right angles.
Rectangle
A parallelogram where all angles are right angles (90°). Its diagonals are equal in length.
Square
A parallelogram that is both a rhombus and a rectangle. All sides are equal and all angles are 90°.
Remember
All rhombuses, rectangles, and squares are parallelograms, but not all parallelograms are rhombuses, rectangles, or squares.
Area of a Parallelogram
The area of a parallelogram is the amount of space inside its boundaries. It's calculated using a simple formula:
Area Formula
Where the base is any side, and the height is the perpendicular distance between that side and its opposite side.
Step 1: Identify the base (b = 8 cm) and height (h = 5 cm)
Step 2: Multiply base by height: 8 × 5 = 40
Step 3: Include units: 40 cm²
So the area is 40 square centimeters.
Remember
The height must be perpendicular to the base. The slant height (side length) is different from the height unless the parallelogram is a rectangle.
Perimeter of a Parallelogram
The perimeter of a parallelogram is the total distance around its outer edges. Since opposite sides are equal, we can calculate it with a simple formula:
Perimeter Formula
Where a and b are the lengths of the adjacent sides (the two different side lengths).
Step 1: Identify the side lengths: a = 7 cm, b = 10 cm
Step 2: Add the sides: 7 + 10 = 17
Step 3: Multiply by 2: 2 × 17 = 34
Step 4: Include units: 34 cm
So the perimeter is 34 centimeters.
Remember
Because opposite sides are equal, you can also calculate perimeter by adding all four sides: a + b + a + b = 2a + 2b = 2(a + b).
Real-World Examples

Parallelograms are all around us! Here are some real-world examples:
Architecture
Many buildings use parallelogram shapes in their design, especially modern architecture with slanted walls.
School Supplies
Some erasers and pencil cases are parallelogram-shaped. Look at your school supplies!
Road Signs
Some warning signs use parallelogram shapes to catch your attention on the road.
Patterns
Tiles, quilts, and many fabric patterns use parallelograms to create interesting designs.
Try This
Look around your classroom or home and see how many parallelogram shapes you can find. Count how many you see in 5 minutes!
Parallelogram Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about parallelograms:
Parallelogram Trivia
Discover interesting facts about parallelograms:
Ancient Geometry
The concept of parallelograms dates back to ancient Greek mathematicians. Euclid described parallelogram properties in his book "Elements" around 300 BCE.
Engineering Strength
Parallelogram shapes are used in bridges and buildings because they distribute weight evenly. The famous Eiffel Tower contains many parallelogram structures.
Crystal Structures
Many minerals form parallelogram-shaped crystals. The mineral calcite often breaks into perfect rhombus-shaped pieces, which are special parallelograms.
Largest Parallelogram
The largest human-made parallelogram is the Shun Hing Square in Shenzhen, China. This skyscraper has a parallelogram shape and stands 384 meters tall.





