Prime Factorization - Definition, Examples, Quiz, FAQ, Trivia
Learn about prime numbers and how to break down numbers into their prime factors
What is Prime Factorization?

Prime factorization is the process of breaking down a composite number into the product of its prime factors.
A prime number is a whole number greater than 1 that has exactly two distinct positive divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, etc.
A composite number is a whole number greater than 1 that has more than two divisors. Composite numbers can be broken down into prime factors.
Every composite number can be expressed as a unique product of prime numbers. This is called the Fundamental Theorem of Arithmetic.
Key Concept
Prime factorization is like breaking down a building into its basic building blocks. Just as a house is made of bricks, composite numbers are made of prime numbers.
Prime Factorization Methods
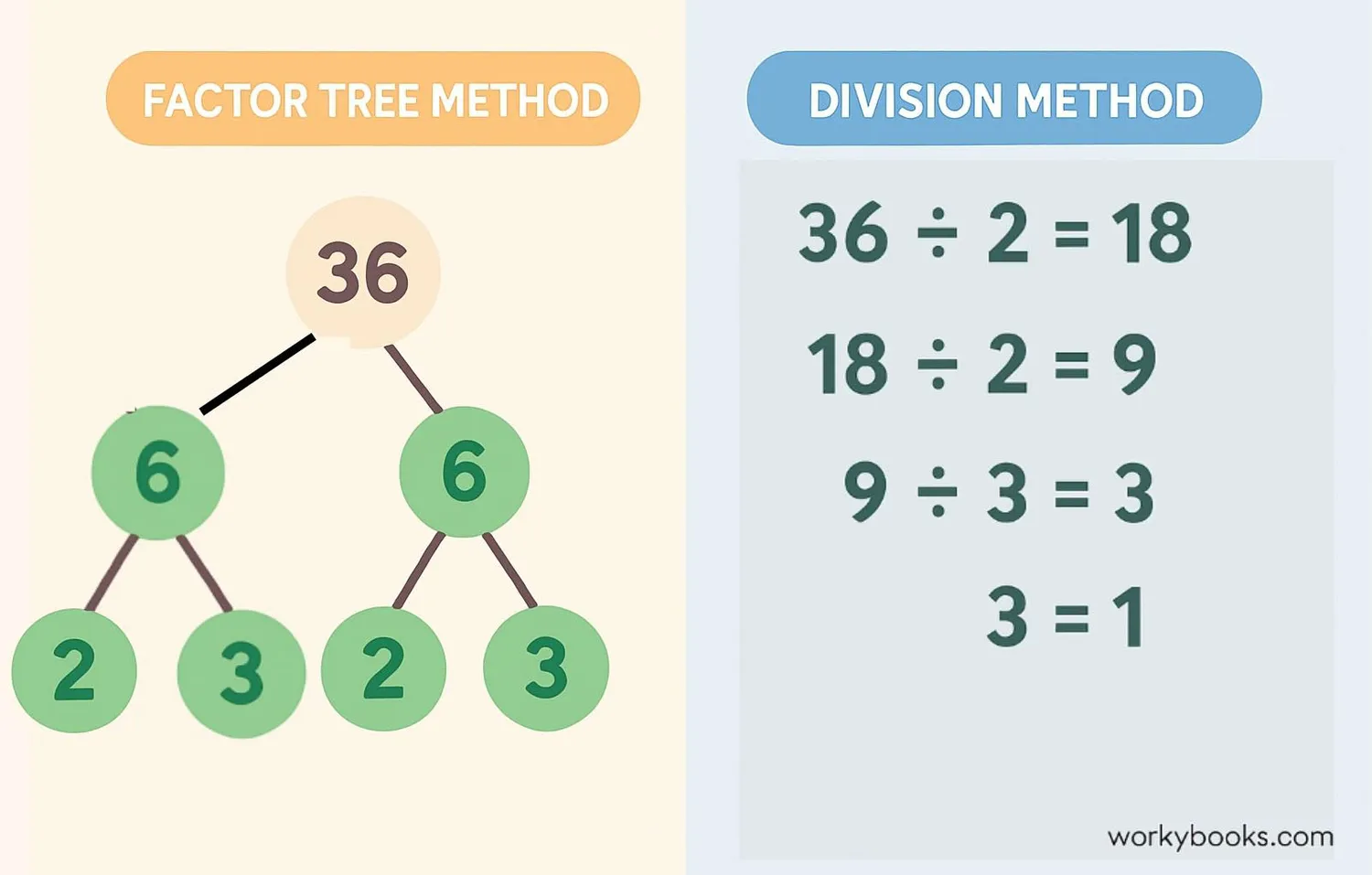
Factor Tree Method
The factor tree method is a visual way to find prime factors. Here's how it works:
- Start with the number you want to factorize at the top
- Find two factors that multiply to make that number
- Continue breaking down each factor until all branches end with prime numbers
- The prime numbers at the bottom are the prime factors
-
36
-
4
- 2
- 2
-
9
- 3
- 3
-
4
36 = 2 × 2 × 3 × 3 = 2² × 3²
Division Method
The division method uses repeated division by prime numbers:
- Divide the number by the smallest prime number possible
- Divide the quotient by the smallest prime number possible
- Continue dividing until the quotient is a prime number
- The divisors are the prime factors
Example: Factorizing 60
30 ÷ 2 = 15
15 ÷ 3 = 5
5 ÷ 5 = 1
60 = 2 × 2 × 3 × 5 = 2² × 3 × 5
Remember
No matter which method you use, the prime factors will always be the same for a given number. This is called the uniqueness of prime factorization.
Prime Factorization Examples
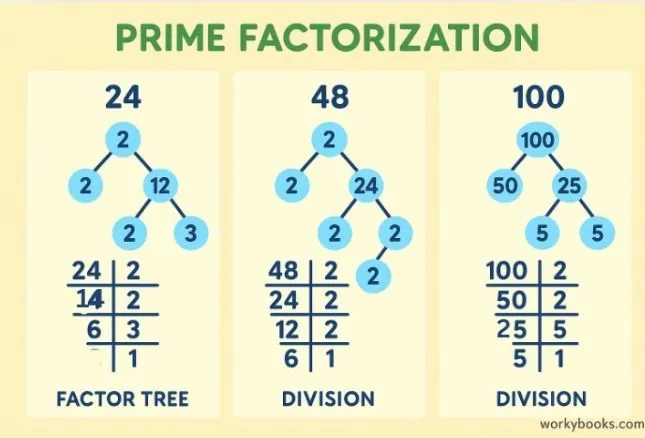
Let's look at some examples of prime factorization:
| Number | Prime Factors | Exponential Form |
|---|---|---|
| 12 | 2 × 2 × 3 | 2² × 3 |
| 24 | 2 × 2 × 2 × 3 | 2³ × 3 |
| 30 | 2 × 3 × 5 | 2 × 3 × 5 |
| 45 | 3 × 3 × 5 | 3² × 5 |
| 60 | 2 × 2 × 3 × 5 | 2² × 3 × 5 |
| 100 | 2 × 2 × 5 × 5 | 2² × 5² |
Pattern Tip
Notice how even numbers always have 2 as a prime factor? Numbers ending with 0 or 5 always have 5 as a prime factor.
Applications of Prime Factorization
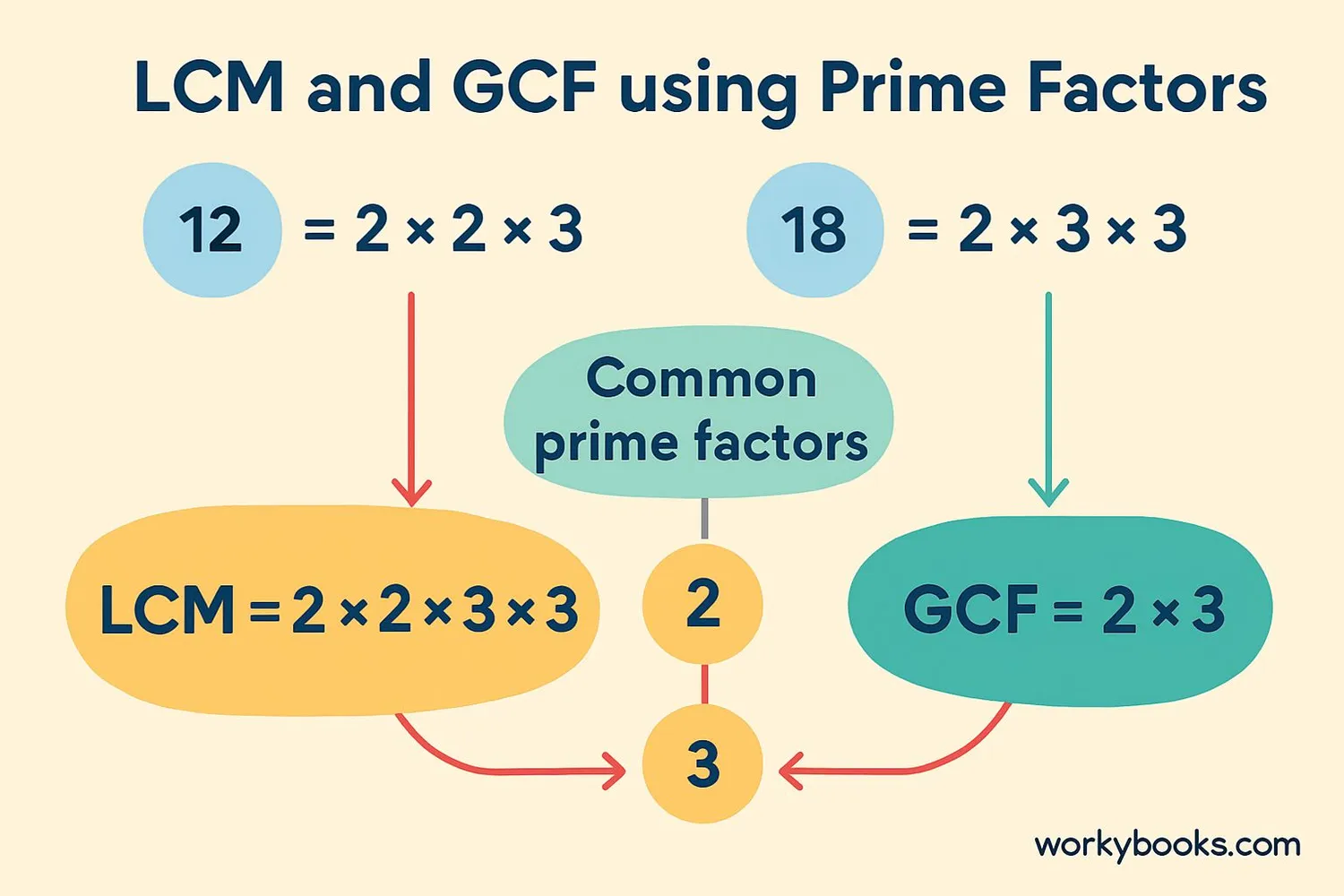
Prime factorization has practical applications in mathematics, especially for finding:
Greatest Common Factor (GCF)
The GCF of two numbers is the largest number that divides both numbers. To find GCF using prime factors:
1. Find the prime factors of each number
2. Identify the common prime factors
3. Multiply the common prime factors (using the lowest power for each)
Example: GCF of 24 and 36
36 = 2² × 3²
GCF = 2² × 3 = 12
Least Common Multiple (LCM)
The LCM of two numbers is the smallest number that is a multiple of both. To find LCM using prime factors:
1. Find the prime factors of each number
2. Take all prime factors (common and uncommon)
3. Use the highest power for each prime factor
Example: LCM of 24 and 36
36 = 2² × 3²
LCM = 2³ × 3² = 8 × 9 = 72
Application Tip
Prime factorization makes finding GCF and LCM much easier, especially for larger numbers.
Prime Factorization Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about prime factorization:
Math Trivia
Discover interesting facts about prime numbers and factorization:
Euclid's Contribution
Euclid, the ancient Greek mathematician, proved that there are infinitely many prime numbers over 2,300 years ago. His elegant proof is still taught in mathematics classes today.
Prime Numbers in Nature
Cicadas use prime numbers in their life cycles! Some species emerge every 13 or 17 years (both prime numbers) to avoid predators with synchronized life cycles.
Prime Numbers in Security
Prime factorization is the basis of modern internet security. Large prime numbers are used in encryption to protect sensitive information like credit card numbers.
Largest Known Prime
The largest known prime number as of 2025 has over 24 million digits! It was discovered through the Great Internet Mersenne Prime Search (GIMPS) project.





