Circle Radius - Definition, Examples, Quiz, FAQ, Trivia
Learn about circle radius with simple explanations, interactive examples, and practice quizzes
What is Circle Radius?
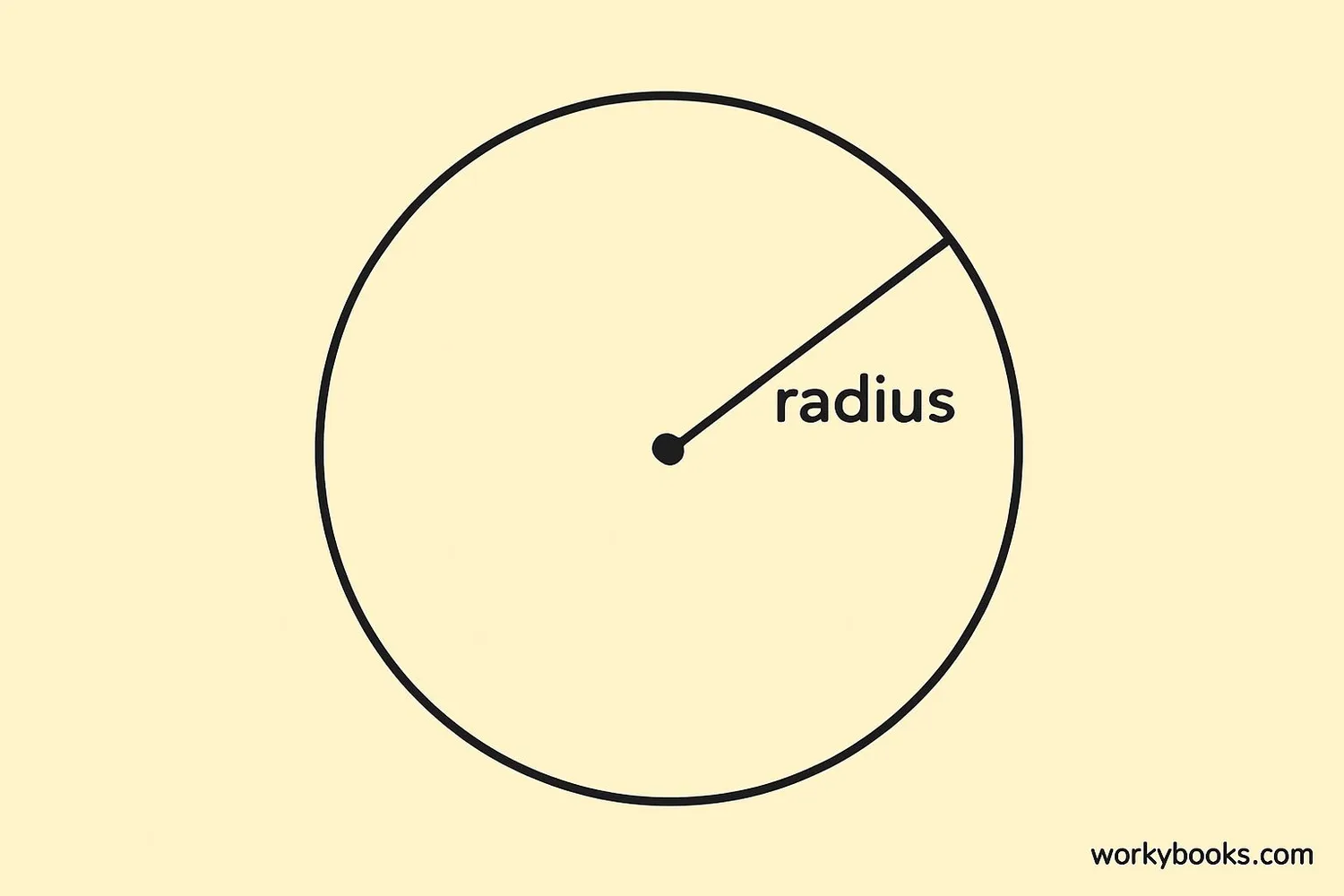
The radius of a circle is the distance from the center point to any point on the edge of the circle.
Think of it like the spoke of a bicycle wheel - each spoke connects the center of the wheel to the outer rim. The length of that spoke is the radius!
Every circle has only one center point, but it has many radii (that's the plural of radius). All radii in a circle are exactly the same length. This is what makes a circle perfectly round!
Key Concept
The radius defines the size of the circle. A larger radius means a larger circle!
How to Find Circle Radius
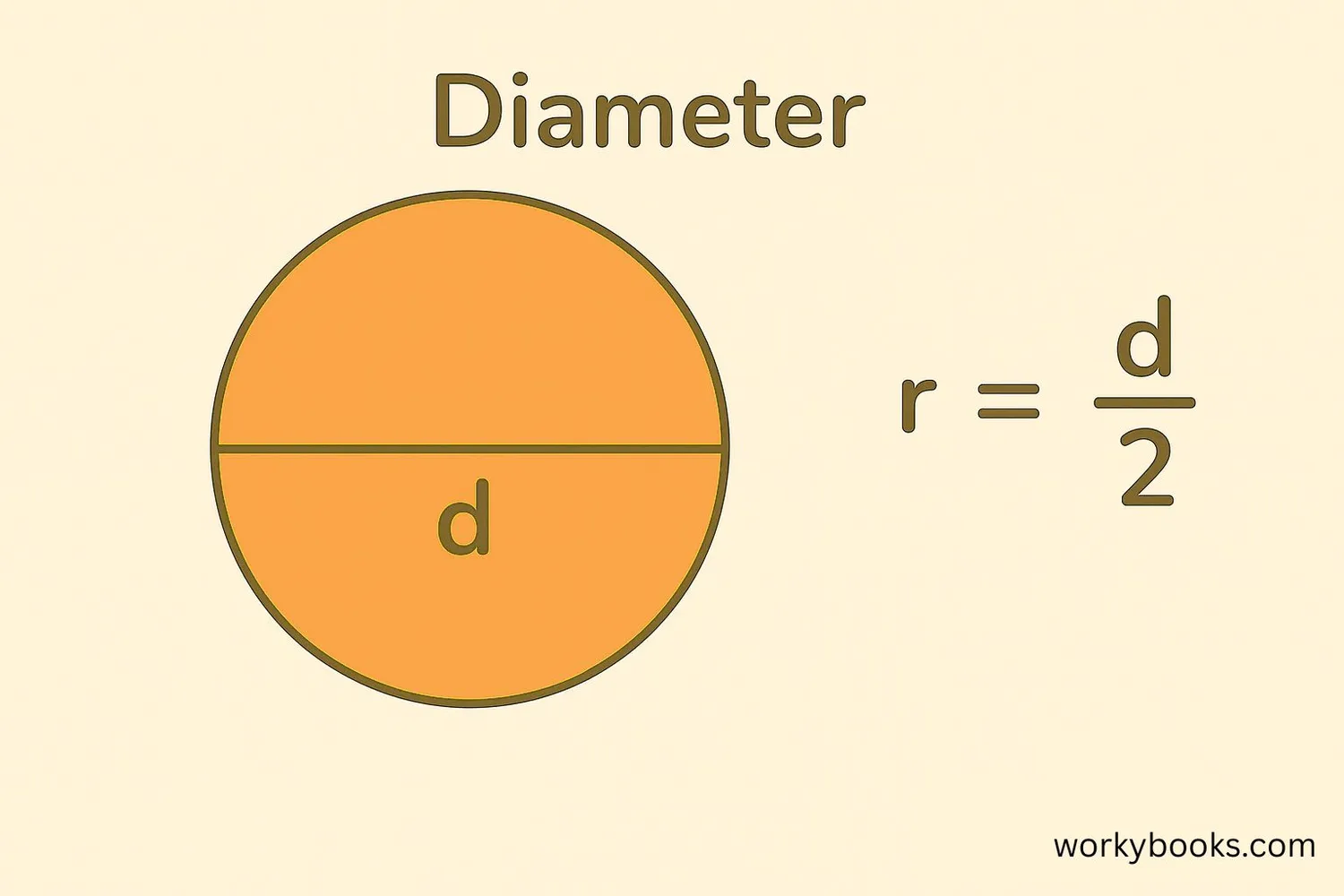
There are several ways to find the radius of a circle:
1. Using Diameter: The diameter is the distance across a circle through its center. The radius is exactly half of the diameter. If you know the diameter, simply divide it by 2 to get the radius.
Radius Formula Using Diameter
Where r is radius and d is diameter
Radius Formula Using Circumference
Where r is radius, C is circumference, and π ≈ 3.14
Radius Formula Using Area
Where r is radius, A is area, and π ≈ 3.14
Remember
π (pi) is a special number in math that represents the ratio of a circle's circumference to its diameter. It's approximately 3.14.
Radius Formulas
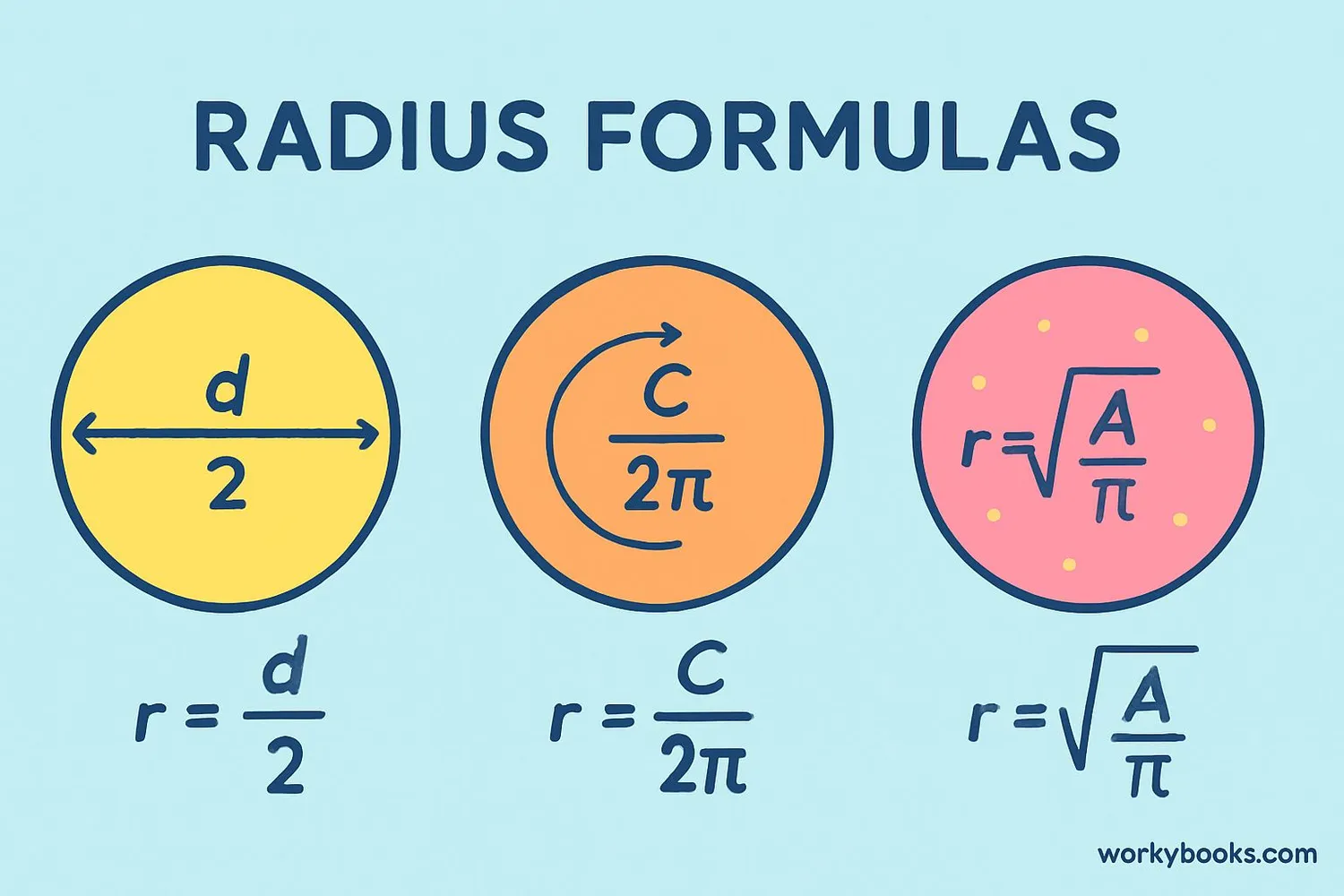
Here's a summary of all the important radius formulas:
| When You Know... | Formula to Find Radius |
|---|---|
| Diameter (d) | r = d ÷ 2 |
| Circumference (C) | r = C ÷ (2 × π) |
| Area (A) | r = √(A ÷ π) |
| Area of Sector (A_s) and Central Angle (θ) | r = √(A_s × 360 ÷ (π × θ)) |
Formula Tip
The diameter formula is the simplest one! If you can measure across a circle, you can find the radius.
Real-World Examples
Let's see how radius works with some real-world examples:
Example 1: A bicycle wheel has a diameter of 60 cm. What is its radius?
Solution: Radius = Diameter ÷ 2 = 60 ÷ 2 = 30 cm
Example 2: A circular swimming pool has a circumference of 31.4 meters. What is its radius?
Solution: Radius = Circumference ÷ (2 × π) = 31.4 ÷ (2 × 3.14) = 31.4 ÷ 6.28 = 5 meters
Example 3: A pizza has an area of 314 cm². What is its radius?
Solution: Radius = √(Area ÷ π) = √(314 ÷ 3.14) = √100 = 10 cm
Example 4: A clock has a minute hand that's 15 cm long. How far does the tip of the minute hand travel in one hour?
Solution: The minute hand is the radius of the circle it travels. In one hour, it makes one full circle.
Circumference = 2 × π × r = 2 × 3.14 × 15 ≈ 94.2 cm
Practice Tip
Look for circles around you and try to estimate their radius. Then measure to check your estimate!
Radius Practice Quiz
Test your understanding of circle radius with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about circle radius:
Circle Trivia
Discover interesting facts about circles and radius:
Ancient Circles
The concept of circles and radius has been known since ancient times. The earliest known wheels, dating back to 3500 BCE, applied circle principles!
The Pi Connection
The number π (pi) has been calculated to over 62 trillion digits! But for most calculations, 3.14 is accurate enough.
Circles in Nature
Circles appear everywhere in nature - from tree rings and raindrop ripples to planets and stars. The circular shape is nature's way of creating efficiency.
Giant Circle
The Sun is approximately 1.4 million kilometers in diameter. That means its radius is about 700,000 kilometers - that's 109 times Earth's radius!





