Reflection in Math - Definition, Examples, Quiz, FAQ, Trivia
Learn about transformations and mirror images with easy explanations and practice activities
What is Reflection?
A reflection is a type of transformation in math that flips a shape over a line to create a mirror image. This line is called the line of reflection.
Think of it like looking at your reflection in a mirror. The original shape is called the pre-image, and the flipped shape is called the image. Reflection doesn't change the size or shape of the figure - it only changes its position and orientation.
Reflection is one of four main transformations in math:
- Translation (sliding a shape)
- Rotation (turning a shape)
- Reflection (flipping a shape)
- Dilation (resizing a shape)
Key Concept
A reflection creates a mirror image of a shape across a line. The distance from any point to the line of reflection is equal to the distance from its image to the line.
How Reflection Works
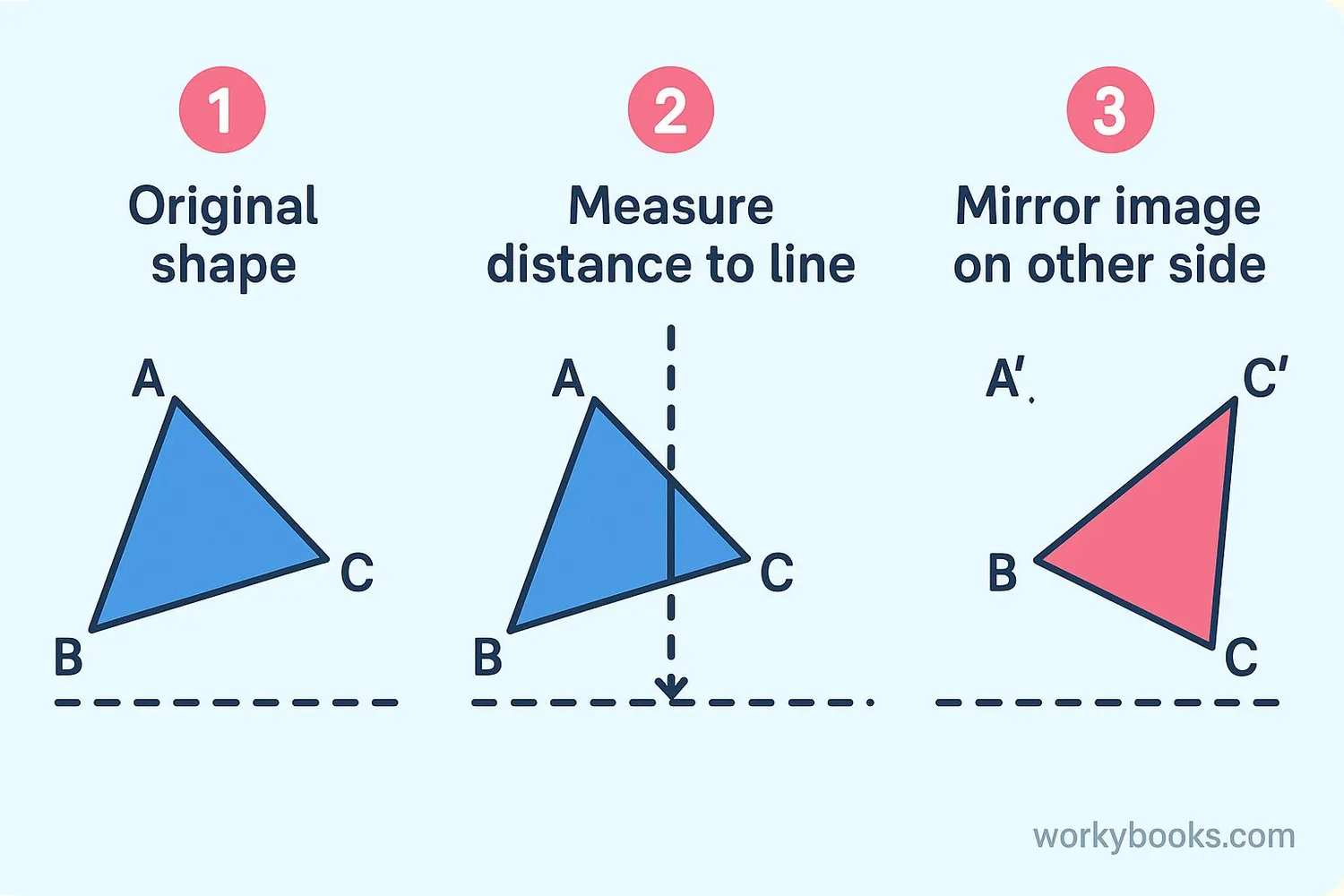
To create a reflection, follow these steps:
- Identify the line of reflection (mirror line)
- For each point in the shape, measure the perpendicular distance to the line
- Place a new point at the same distance on the opposite side of the line
- Connect the new points to form the reflected shape
Remember
Reflection is like folding paper along the mirror line - points that match up after folding are reflections of each other.
Reflection on Coordinate Plane
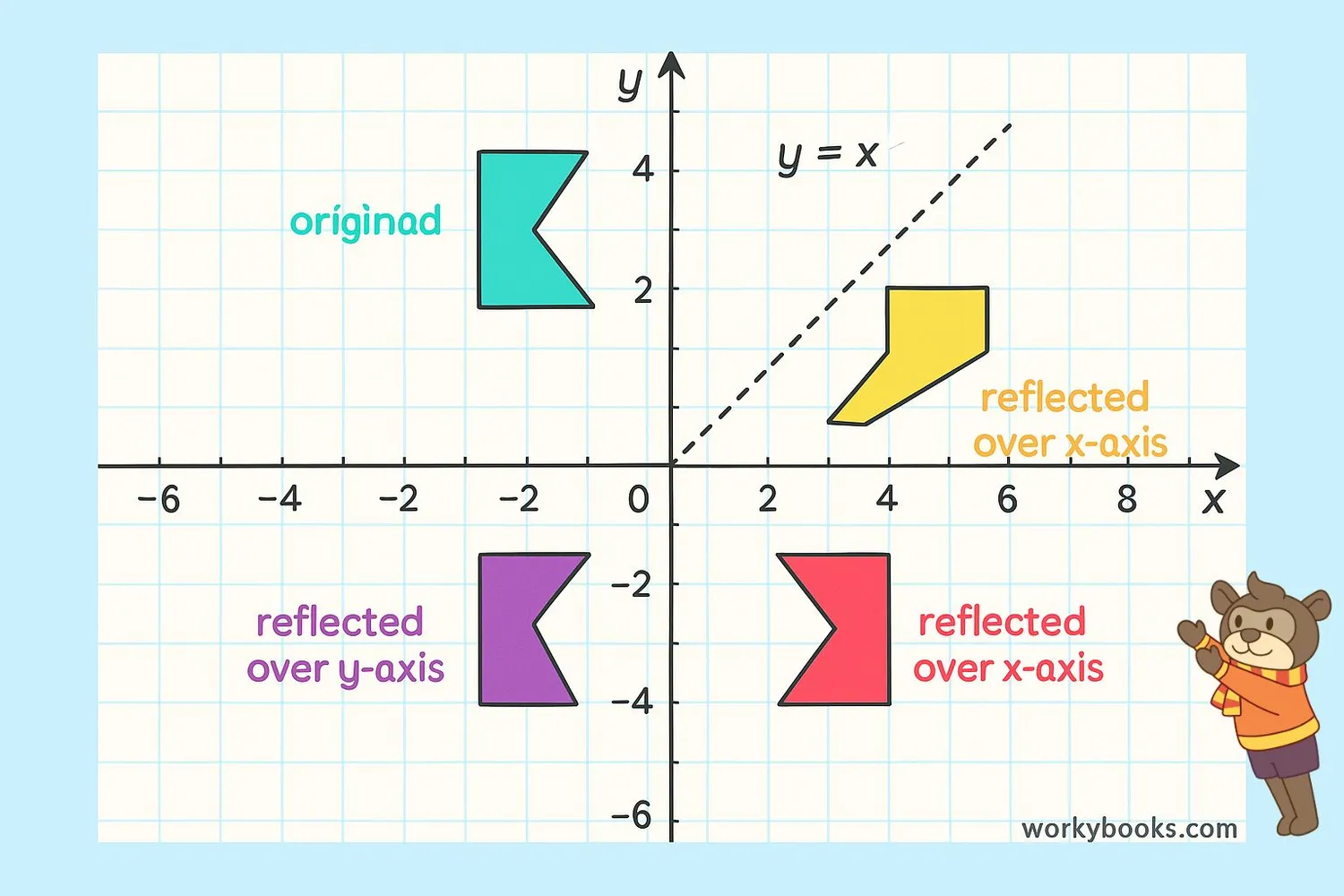
On a coordinate plane, we can reflect shapes over different lines using special rules:
Reflection Rules
Reflection Over X-axis
When reflecting over the x-axis, the x-coordinate stays the same, but the y-coordinate changes sign. For example:
Point (3, 4) reflected over x-axis becomes (3, -4)
Reflection Over Y-axis
When reflecting over the y-axis, the y-coordinate stays the same, but the x-coordinate changes sign. For example:
Point (3, 4) reflected over y-axis becomes (-3, 4)
Coordinate Tip
Reflecting over both axes (origin reflection) changes both signs: (x, y) becomes (-x, -y).
Real-World Examples

Reflection isn't just a math concept - we see it everywhere in the real world:
Example 1: Butterfly wings are symmetrical - each side is a reflection of the other.
Example 2: When you look in a mirror, you see a reflection of yourself.
Example 3: Many buildings and bridges have reflective symmetry in their design.
Example 4: Letters like A, M, T, U, V, W, and Y have reflection symmetry.
Math Example
Reflect the triangle with points A(2,3), B(4,1), C(5,4) over the y-axis:
Solution:
- A(2,3) → A'(-2,3)
- B(4,1) → B'(-4,1)
- C(5,4) → C'(-5,4)
Symmetry Tip
If a shape can be folded along a line so that both halves match exactly, it has reflection symmetry.
Reflection Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about reflection in math:
Math Trivia
Discover interesting facts about reflection and symmetry:
Symmetry in Nature
Most animals have bilateral symmetry (reflection symmetry) because it helps with balance and movement. Even the human body has approximate reflection symmetry!
Architectural Symmetry
Famous buildings like the Taj Mahal and the U.S. Capitol use reflection symmetry in their design to create a sense of balance and beauty.
Art and Reflection
Artist M.C. Escher created famous works using reflection and other transformations. His art shows fish transforming into birds through reflection and other symmetry operations.
Molecular Symmetry
In chemistry, molecules often have reflection symmetry. Understanding molecular symmetry helps scientists predict how molecules will behave and interact.





