Repeating Decimal to Fraction - Definition, Examples, Quiz, FAQ, Trivia
Learn to convert repeating decimals to fractions with easy explanations and practice activities
What is a Repeating Decimal?

A repeating decimal is a decimal number where a digit or group of digits repeats forever. We show repeating digits with a bar above them. For example:
0.333... is written as 0.3̄ (the 3 repeats forever)
0.121212... is written as 0.1̄2̄ (the "12" repeats forever)
Repeating decimals are also called recurring decimals. They represent rational numbers, which means they can be converted to fractions. The repeating part can be a single digit or a group of digits.
Key Concept
All repeating decimals can be expressed as fractions of integers. This is why they're called rational numbers!
How to Convert Repeating Decimals to Fractions
Converting repeating decimals to fractions might seem tricky, but it's easy once you learn the steps. Here's the method:
Identify the Repeating Part
Determine which digits repeat. For example, in 0.777..., the repeating part is "7". In 0.454545..., the repeating part is "45".
Assign a Variable
Set the decimal equal to a variable. For example, let x = 0.777...
Multiply by 10n
Multiply both sides by 10 raised to the power of the number of repeating digits. For one repeating digit (like 7), multiply by 10. For two repeating digits (like 45), multiply by 100.
Subtract the Original Equation
Subtract the original equation from the multiplied equation. This eliminates the repeating part.
Solve for x
Solve the resulting equation for x and simplify the fraction.
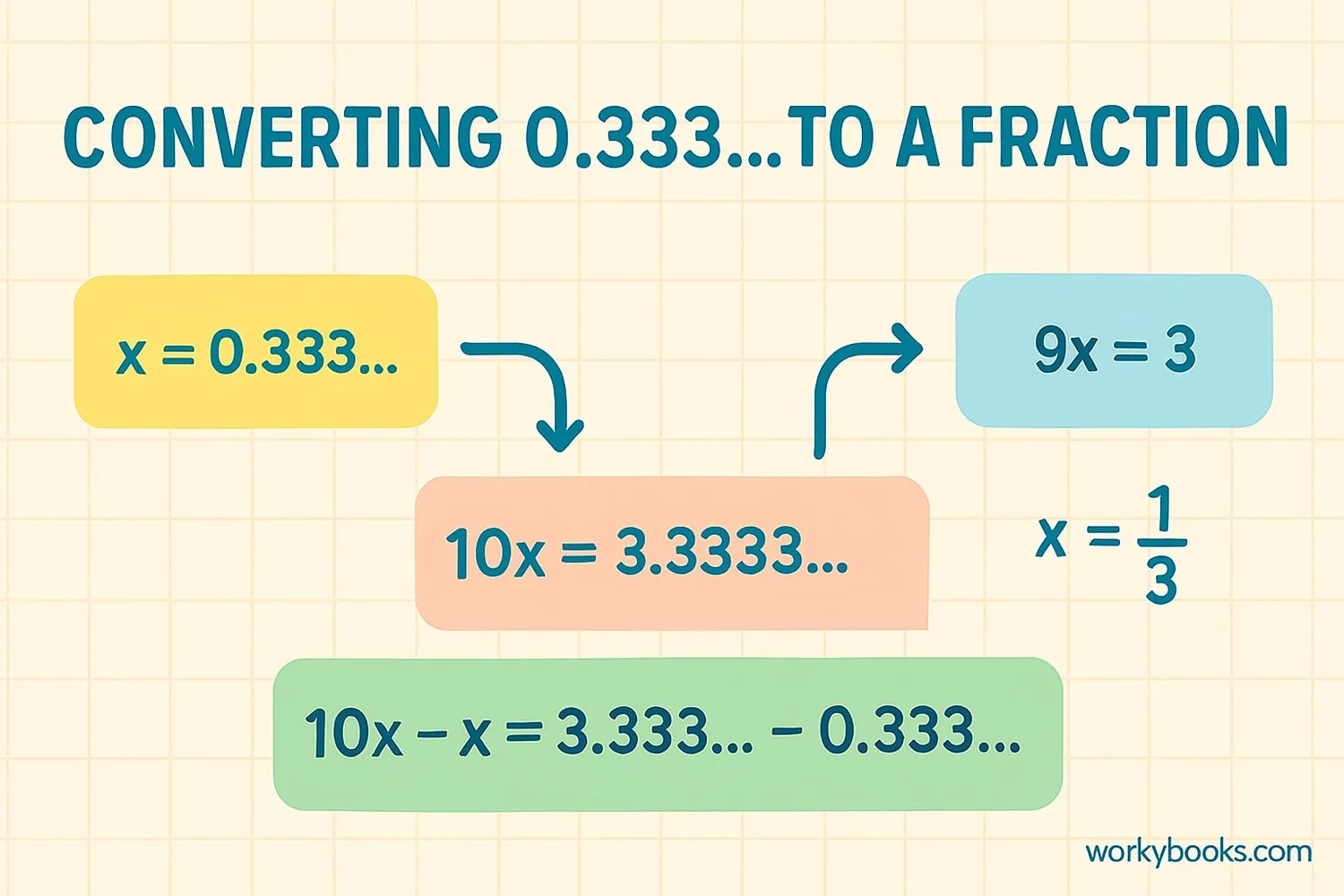
Step 1: Let x = 0.333...
Step 2: Multiply by 10: 10x = 3.333...
Step 3: Subtract: 10x - x = 3.333... - 0.333... → 9x = 3
Step 4: Solve: x = 3/9 = 1/3
Therefore, 0.333... = 1/3
Conversion Formula
The key is to eliminate the repeating part through multiplication and subtraction.
Conversion Tricks and Chart

Here are some useful tricks and patterns for converting repeating decimals to fractions:
Trick 1: For a single repeating digit after the decimal, the fraction is that digit over 9.
Example: 0.444... = 4/9
Trick 2: For two repeating digits, the fraction is those digits over 99.
Example: 0.272727... = 27/99 = 3/11
Trick 3: For decimals with non-repeating parts before the repeating part, adjust accordingly.
Example: 0.1333... = 0.13̄ = 2/15
Common Repeating Decimals to Fractions Chart
| Repeating Decimal | Fraction | Simplified Fraction |
|---|---|---|
| 0.111... | 1/9 | 1/9 |
| 0.222... | 2/9 | 2/9 |
| 0.333... | 3/9 | 1/3 |
| 0.444... | 4/9 | 4/9 |
| 0.555... | 5/9 | 5/9 |
| 0.666... | 6/9 | 2/3 |
| 0.777... | 7/9 | 7/9 |
| 0.888... | 8/9 | 8/9 |
| 0.0909... | 9/99 | 1/11 |
| 0.1818... | 18/99 | 2/11 |
| 0.2727... | 27/99 | 3/11 |
| 0.3636... | 36/99 | 4/11 |
Pattern Tip
Notice how the denominator always has as many 9s as there are repeating digits? That's the key pattern!
Conversion Examples

Let's practice with more examples of converting repeating decimals to fractions:
Step 1: Let x = 0.666...
Step 2: Multiply by 10: 10x = 6.666...
Step 3: Subtract: 10x - x = 6.666... - 0.666... → 9x = 6
Step 4: Solve: x = 6/9 = 2/3
Therefore, 0.666... = 2/3
Step 1: Let x = 0.121212...
Step 2: Multiply by 100 (two repeating digits): 100x = 12.121212...
Step 3: Subtract: 100x - x = 12.121212... - 0.121212... → 99x = 12
Step 4: Solve: x = 12/99 = 4/33
Therefore, 0.121212... = 4/33
Step 1: Let x = 0.4555...
Step 2: Multiply by 10: 10x = 4.555...
Step 3: Multiply by 100: 100x = 45.555...
Step 4: Subtract: 100x - 10x = 45.555... - 4.555... → 90x = 41
Step 5: Solve: x = 41/90
Therefore, 0.4555... = 41/90
Conversion Tip
Always simplify your fractions at the end. For example, 3/9 simplifies to 1/3!
Practice Quiz
Test your conversion skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about repeating decimals and fractions:
Math Trivia
Discover interesting facts about decimals and fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They had special symbols for fractions like 1/2, 1/3, and 1/4, but all other fractions were expressed as sums of these unit fractions.
Decimal Point Invention
The decimal point was invented by John Napier, a Scottish mathematician, in the early 17th century. Before this, fractions were the primary way to represent parts of a whole.
Infinite Fractions
The fraction 1/7 has a fascinating repeating decimal: 0.142857142857... This six-digit pattern repeats endlessly. If you multiply this fraction by 2, 3, etc., you get cyclic permutations of the same digits!
Longest Repeating Decimal
The fraction 1/97 has the longest repeating cycle for a denominator less than 100. Its decimal has 96 repeating digits! The length of the repeating cycle for 1/n can be up to n-1 digits.





