Geometric Transformations - Definition, Examples, Quiz, FAQ, Trivia
Learn how shapes move, turn, flip and change size with translation, rotation, reflection and dilation
What are Geometric Transformations?
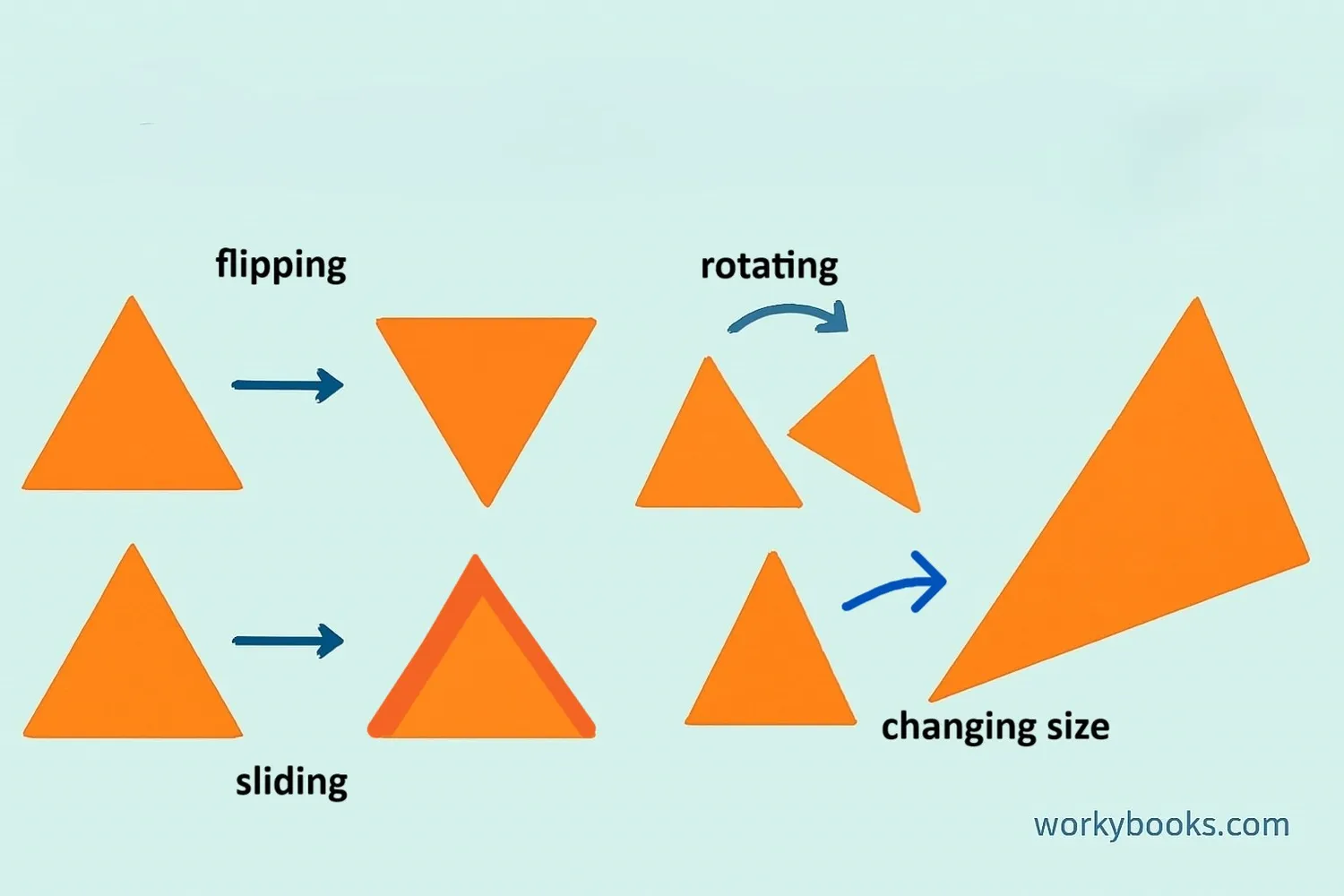
Geometric transformations are like magic tricks we can do with shapes! They change a shape's position, size, or direction without changing its basic form. Think of it as moving furniture in a room - the furniture stays the same, but its location changes.
In math, we call the original shape the pre-image and the transformed shape the image. Transformations help us understand how shapes relate to each other in space, which is important in art, architecture, and video games!
There are four main types of transformations:
- Translation - Sliding a shape without turning it
- Rotation - Turning a shape around a point
- Reflection - Flipping a shape over a line
- Dilation - Making a shape bigger or smaller
Key Concept
Transformations change a shape's position or size but keep its essential properties. The pre-image is the original shape, and the image is the transformed shape.
Types of Transformations
Let's explore the four main types of geometric transformations. Each one does something special to shapes!
Translation
Definition: Translation means sliding a shape from one place to another without turning or flipping it. Every point of the shape moves the same distance in the same direction.
Example: Like sliding a book across a table, or a chess piece moving to a new square.
Rotation
Definition: Rotation means turning a shape around a fixed point called the center of rotation. The shape stays the same size, but its direction changes.
Example: Like the hands of a clock turning, or spinning a toy top.
Reflection
Definition: Reflection means flipping a shape over a line to create a mirror image. The reflected shape is the same size but faces the opposite direction.
Example: Like your reflection in a mirror, or butterfly wings.
Dilation
Definition: Dilation means resizing a shape to make it bigger or smaller. The shape keeps the same proportions but changes size.
Example: Like zooming in on a picture, or a movie projector making an image larger.
Remember
Translation, rotation, and reflection are rigid transformations - they preserve size and shape. Dilation is non-rigid - it preserves shape but not size.
Properties & Rules
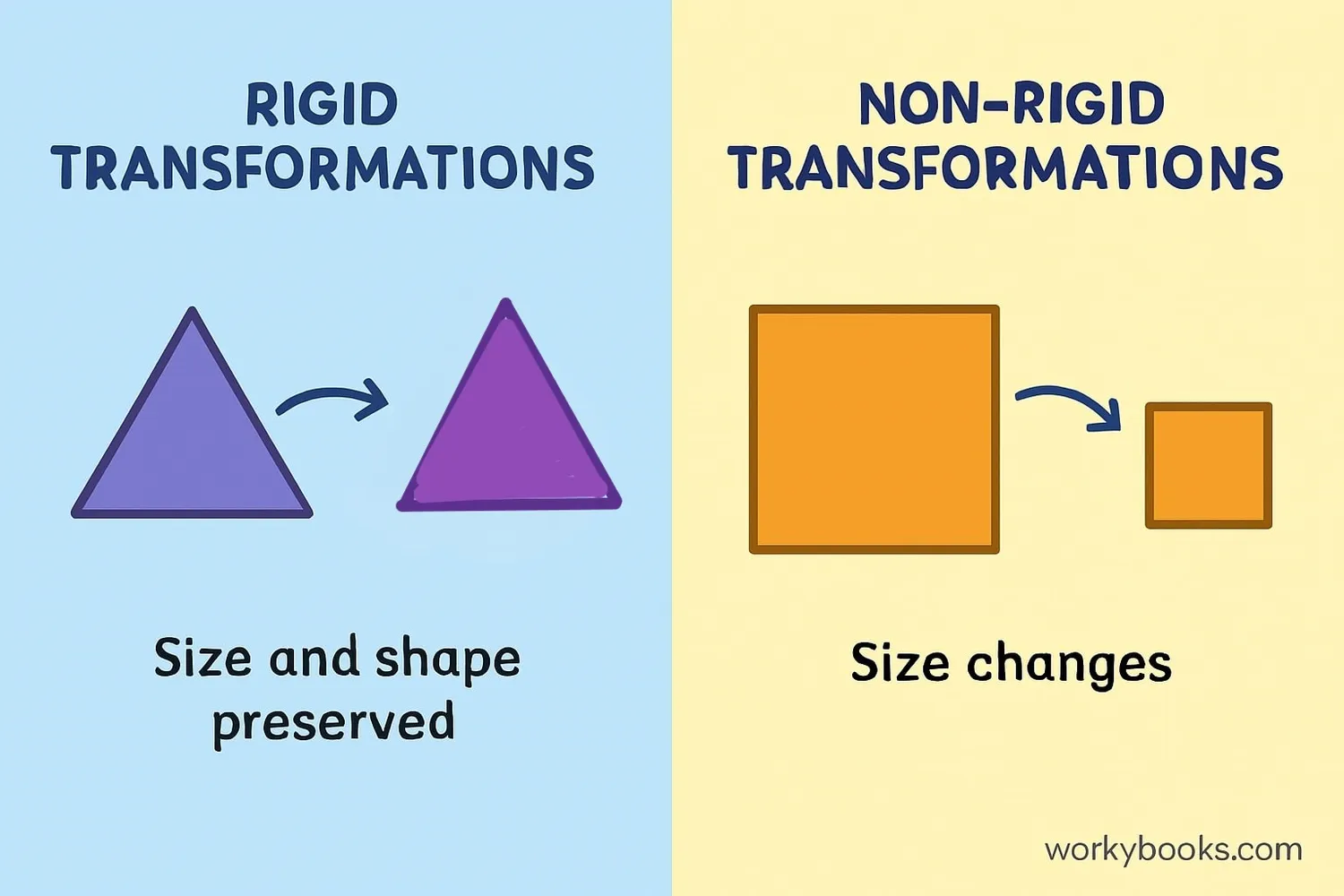
Transformations have special properties that help us understand how shapes change:
Rigid Transformations
These transformations preserve size and shape. The pre-image and image are congruent (exactly the same size and shape).
- Translation
- Rotation
- Reflection
Non-Rigid Transformations
These transformations preserve shape but not size. The pre-image and image are similar (same shape but different size).
- Dilation
Transformation Rules
On a coordinate plane, we use special rules to describe transformations:
Translation: (x, y) → (x + a, y + b)
Moves a units right and b units up
Rotation (90° clockwise): (x, y) → (y, -x)
Reflection (over y-axis): (x, y) → (-x, y)
Dilation: (x, y) → (kx, ky)
Where k is the scale factor
Real-World Examples
Transformations are all around us! Here are some examples of how we see them in everyday life:
Translation
- A car moving down a straight road
- Sliding a drawer open
- A hockey puck sliding across the ice
Rotation
- Ferris wheel turning
- Earth rotating on its axis
- Turning a doorknob
Reflection
- Mountains reflected in a lake
- Butterfly wings
- Mirror images
Dilation
- Zooming in on a map
- Projector making an image larger
- Scale models of buildings
Interactive Transformation Example
Practice Tip
Look for transformations in your environment! Notice how doors rotate, how shadows dilate, and how reflections appear in water.
Transformation Practice Quiz
Test your knowledge of geometric transformations with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about geometric transformations:
Transformation Trivia
Discover interesting facts about geometric transformations:
Ancient Origins
The concept of geometric transformations dates back to ancient Greece. Euclid described transformations in his work "Elements" around 300 BC.
Nature's Transformations
Many flowers exhibit rotational symmetry, while butterflies display reflection symmetry. Snowflakes often have 6-fold rotational symmetry.
Art and Transformation
M.C. Escher, the famous artist, used transformations like translation, rotation, and reflection to create his mind-bending artworks.
Digital Transformations
Every time you pinch to zoom on a smartphone or rotate an image, you're using transformation mathematics in action!





