Transversal - Definition, Examples, Quiz, FAQ, Trivia
Learn about transversals, angle relationships, and properties with visual examples and practice activities
What is a Transversal?
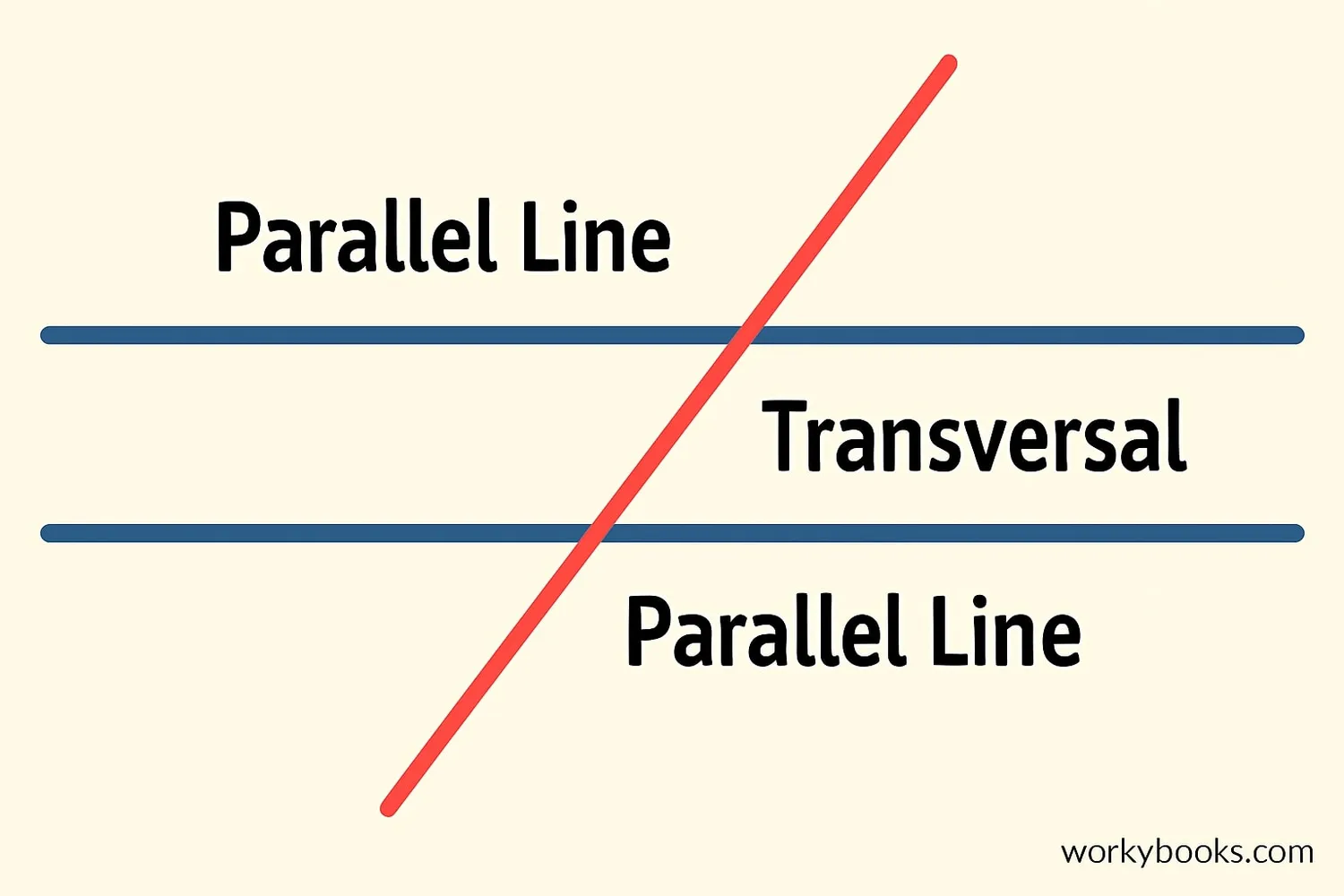
A transversal is a line that crosses two or more other lines at different points. When it crosses parallel lines, special angle relationships are formed that help us solve geometry problems.
Imagine railroad tracks (the parallel lines) and a road crossing them (the transversal). The angles formed at the crossing points have special names and relationships that we'll explore.
Transversals are important in geometry because they help us understand how lines interact and create patterns of angles that always follow specific rules when the lines are parallel.
Key Concept
A transversal must cross at least two lines, but it can cross more. The most interesting relationships happen when it crosses parallel lines.
Angle Relationships
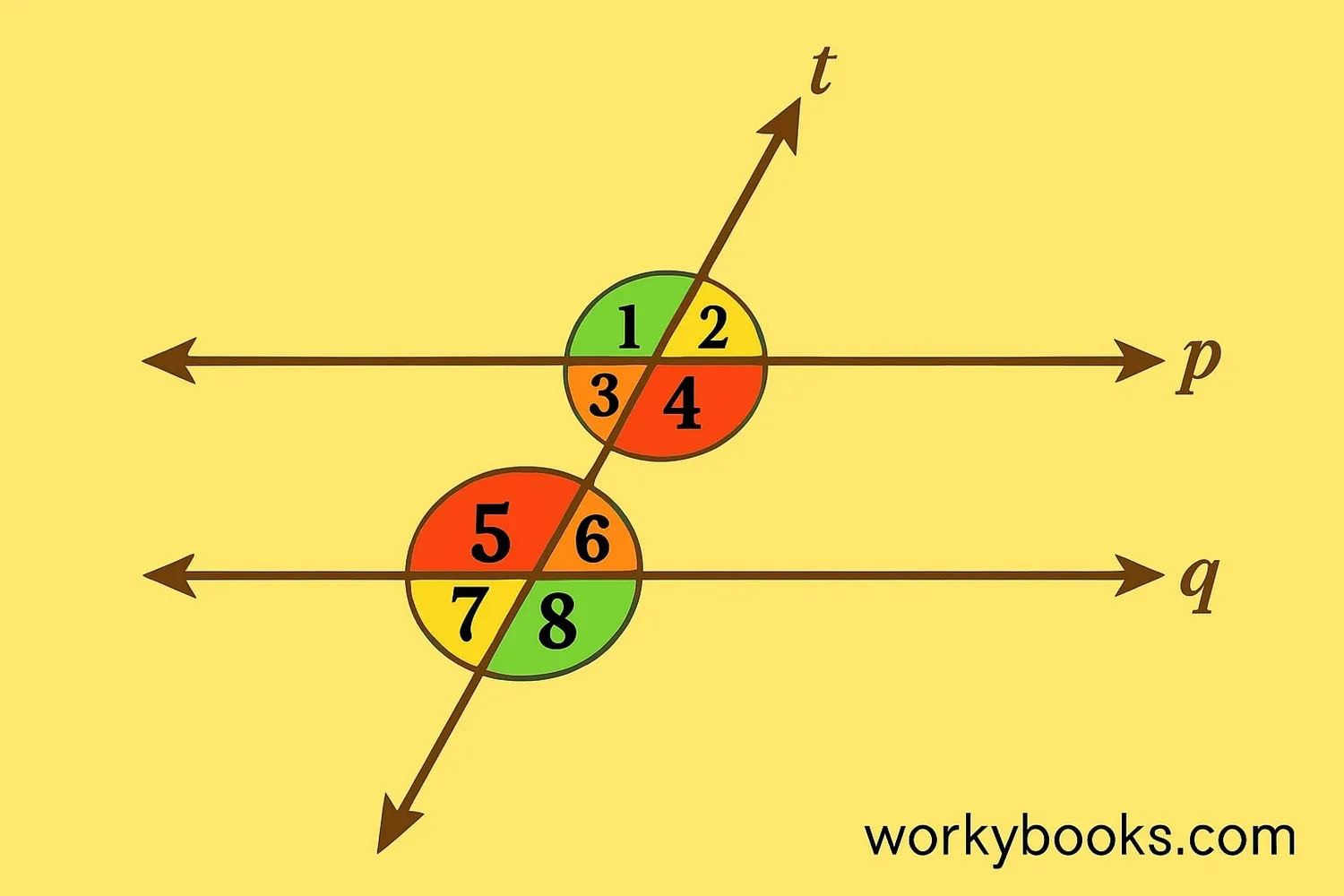
When a transversal crosses two parallel lines, it creates eight angles. These angles have special relationships:
Corresponding Angles
Angles in the same position at each intersection. They are equal when lines are parallel. Example: ∠1 and ∠5, ∠2 and ∠6.
Alternate Interior Angles
Angles inside the parallel lines but on opposite sides of the transversal. They are equal. Example: ∠3 and ∠6, ∠4 and ∠5.
Alternate Exterior Angles
Angles outside the parallel lines but on opposite sides of the transversal. They are equal. Example: ∠1 and ∠8, ∠2 and ∠7.
Consecutive Interior Angles
Angles inside the parallel lines and on the same side of the transversal. They add up to 180°. Example: ∠3 and ∠5, ∠4 and ∠6.
Vertically Opposite Angles
Angles opposite each other when two lines cross. They are always equal. Example: ∠1 and ∠4, ∠2 and ∠3.
Remember
These special relationships only hold true when the transversal crosses parallel lines. If the lines aren't parallel, the angles won't follow these rules.
Properties of Transversals
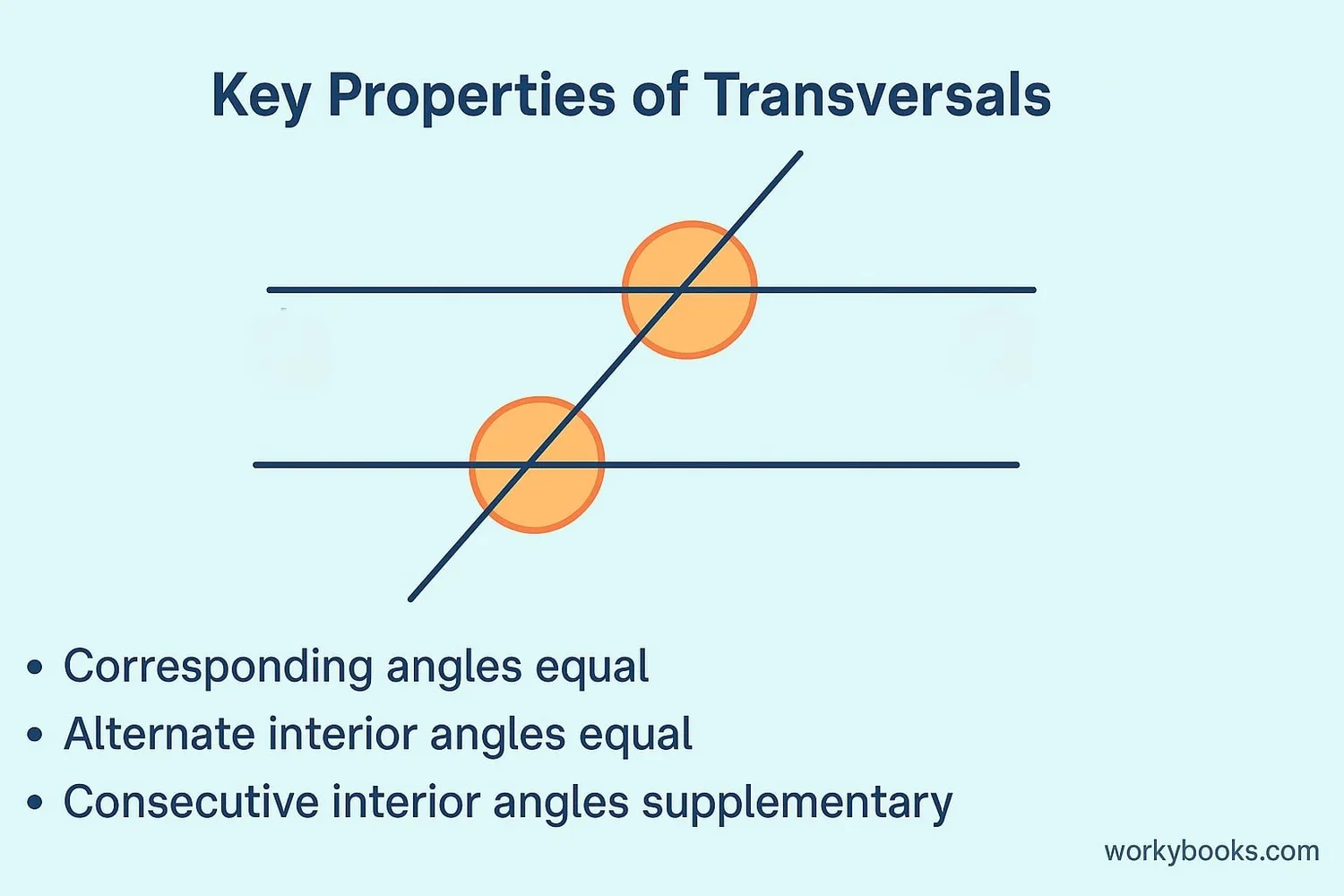
Transversals have special properties when they cross parallel lines. These properties help us solve geometry problems:
Fundamental Properties
- Corresponding angles are equal
- Alternate interior angles are equal
- Alternate exterior angles are equal
- Consecutive interior angles add up to 180°
- Vertically opposite angles are always equal
These properties are like a secret code that helps us find missing angles without measuring. If we know one angle, we can find all the others using these rules!
For example, if we know that two lines are parallel and a transversal crosses them, and we know one angle is 60°, we can find all the other angles using these properties.
Pro Tip
When solving problems, look for these special angle pairs first. They often provide the key to unlocking the solution.
Examples and Applications
Let's see how we use transversal properties to solve problems:
Example 1: Two parallel lines are crossed by a transversal. If one angle is 70°, what is its corresponding angle?
Solution: Corresponding angles are equal, so the corresponding angle is also 70°.
Example 2: In the same setup, what is the alternate interior angle to the 70° angle?
Solution: Alternate interior angles are equal, so it's also 70°.
Example 3: What is the consecutive interior angle to the 70° angle?
Solution: Consecutive interior angles add up to 180°, so 180° - 70° = 110°.
Example 4: A real-world application: In bridge design, engineers use transversal properties to ensure structural integrity. The angles formed by support beams must follow these geometric rules to distribute weight properly.
Practice Tip
Draw the parallel lines and transversal, then label all angles starting from one known angle. The properties will help you fill in the rest!
Practice Quiz
Test your understanding of transversals with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about transversals:
Geometry Trivia
Discover interesting facts about transversals and geometry:
Ancient Geometry
The concept of transversals dates back to ancient Greek mathematicians. Euclid described properties of transversals in his foundational work "Elements" around 300 BCE.
In Nature
Transversal patterns appear in nature, such as in the arrangement of leaves on a stem (phyllotaxis) and the structure of crystals, demonstrating mathematical patterns in the natural world.
Engineering Applications
Engineers use transversal properties when designing bridges, buildings, and roads to ensure structural integrity and proper weight distribution.
In Art and Design
Artists and designers use transversal principles in perspective drawing to create the illusion of depth and in patterns for textiles and architecture.





