Volume of a Cylinder - Definition, Examples, Quiz, FAQ, Trivia
Learn to calculate cylinder volume with formulas, examples, and practice activities
What is Cylinder Volume?
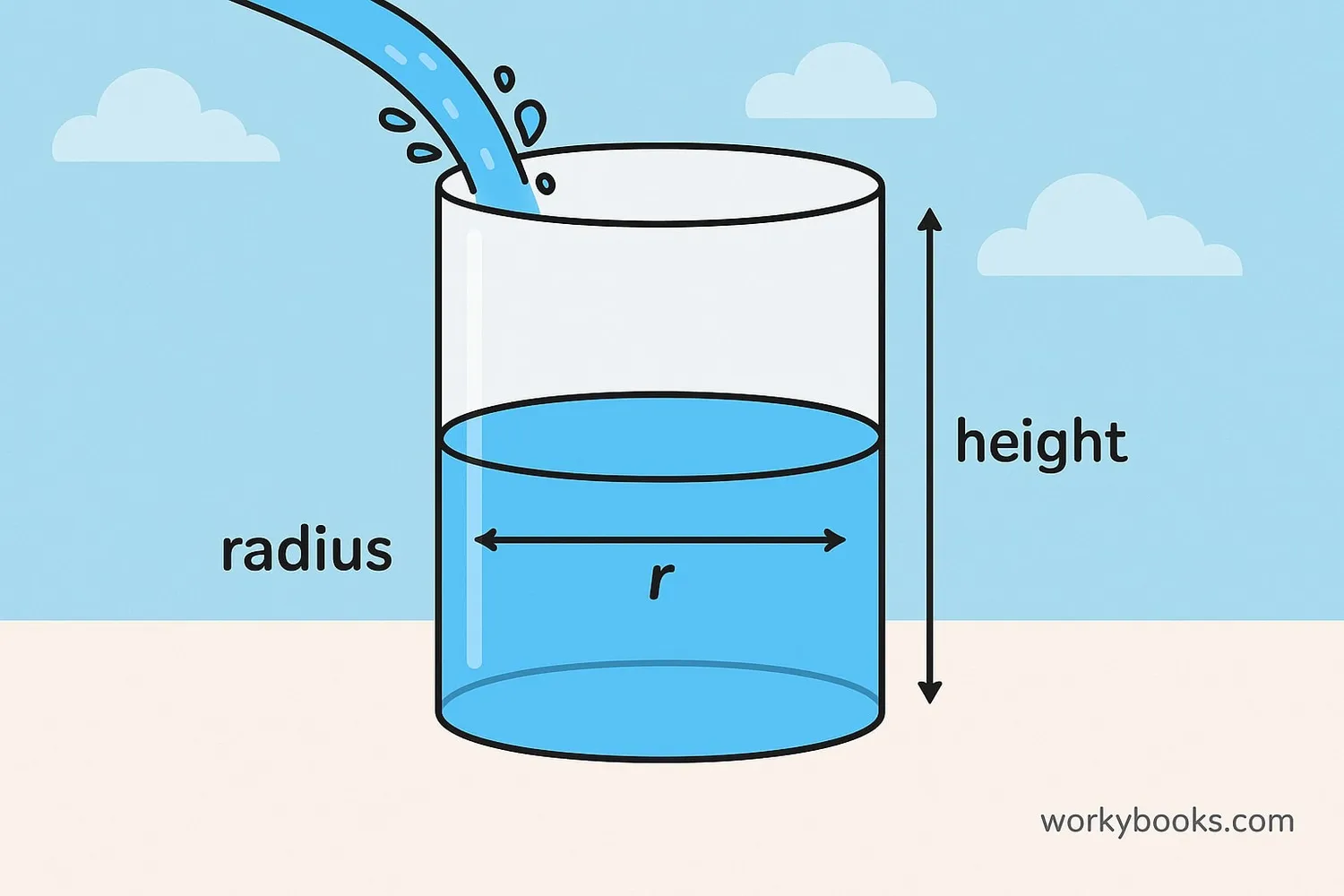
The volume of a cylinder is the amount of space it takes up. It tells us how much the cylinder can hold inside it. Volume is measured in cubic units like cubic centimeters (cm³) or cubic meters (m³).
A cylinder has two important measurements:
• Radius (r) - The distance from the center to the edge of the circular base
• Height (h) - The distance between the two circular bases
Understanding volume helps us solve real problems like:
- How much water a water bottle can hold
- How much grain fits in a silo
- How much paint is needed for a pipe
Key Concept
Volume = Base Area × Height. For cylinders, the base is a circle, so we use πr² for the base area.
How to Calculate Cylinder Volume
To find the volume of any cylinder, we use this formula:
Volume Formula
Where:
V = Volume
π ≈ 3.14 (pi, a special number)
r = radius of the base
h = height of the cylinder
Example: A cylinder has a radius of 4 cm and height of 10 cm. What is its volume?
Step 1: Write the formula → V = πr²h
Step 2: Plug in values → V = 3.14 × (4)² × 10
Step 3: Calculate → V = 3.14 × 16 × 10 = 502.4 cm³
So the cylinder's volume is 502.4 cubic centimeters.
Remember
Radius is half the diameter. If you know diameter, divide it by 2 to get radius before using the formula.
Volume for Different Cylinders
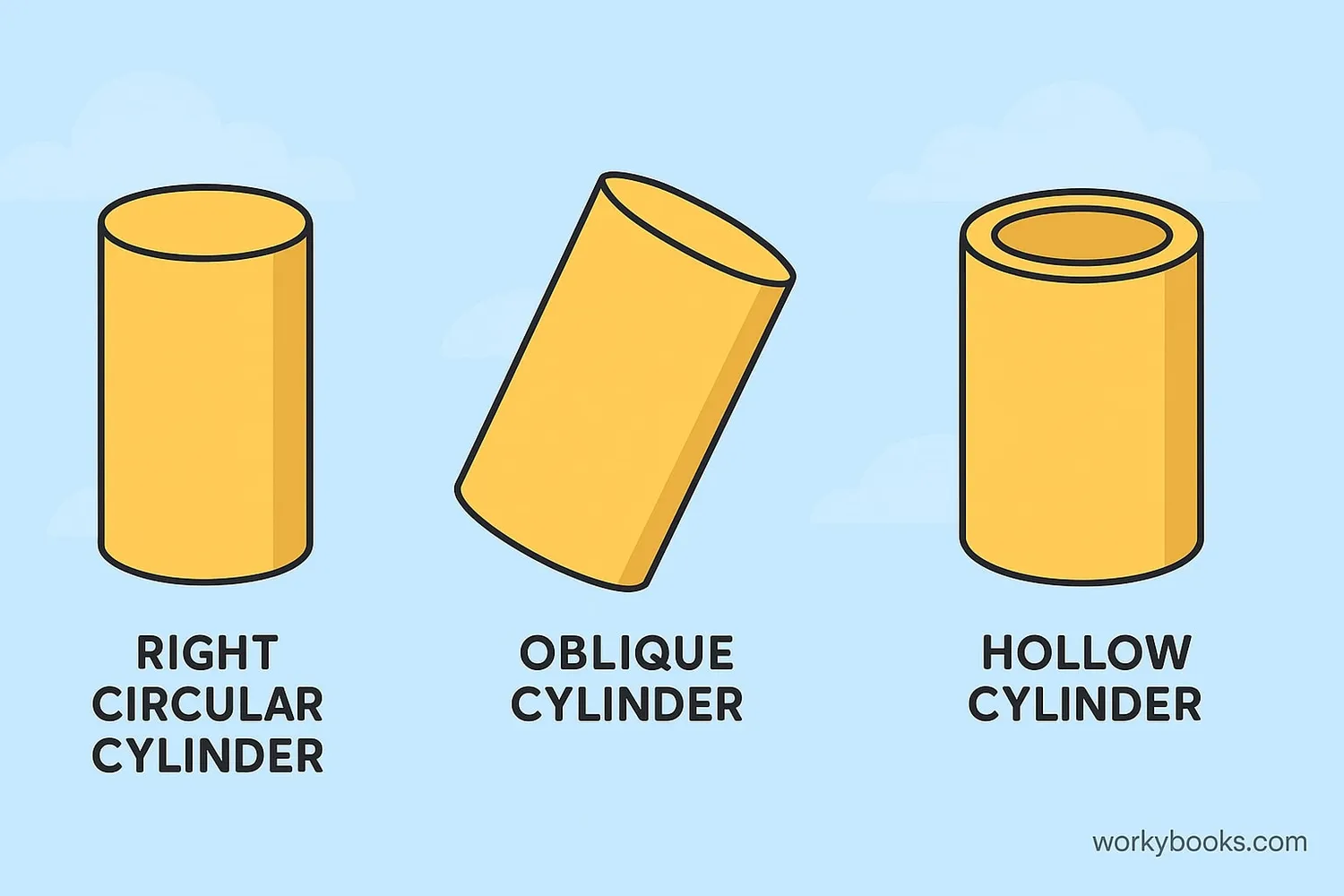
There are different types of cylinders, but the volume formula works for most of them:
Right Circular Cylinder:
This is the standard cylinder with straight sides perpendicular to the bases. Use V = πr²h
Oblique Cylinder:
This cylinder has slanted sides, but as long as the cross-section is circular, we still use V = πr²h
Hollow Cylinder:
For cylinders with an empty center (like a pipe), we subtract the inner cylinder volume:
V = πh(R² - r²) where R is outer radius and r is inner radius
Important Note
For any cylinder, as long as the cross-section is circular and uniform, the volume formula V = πr²h works!
Real-World Examples
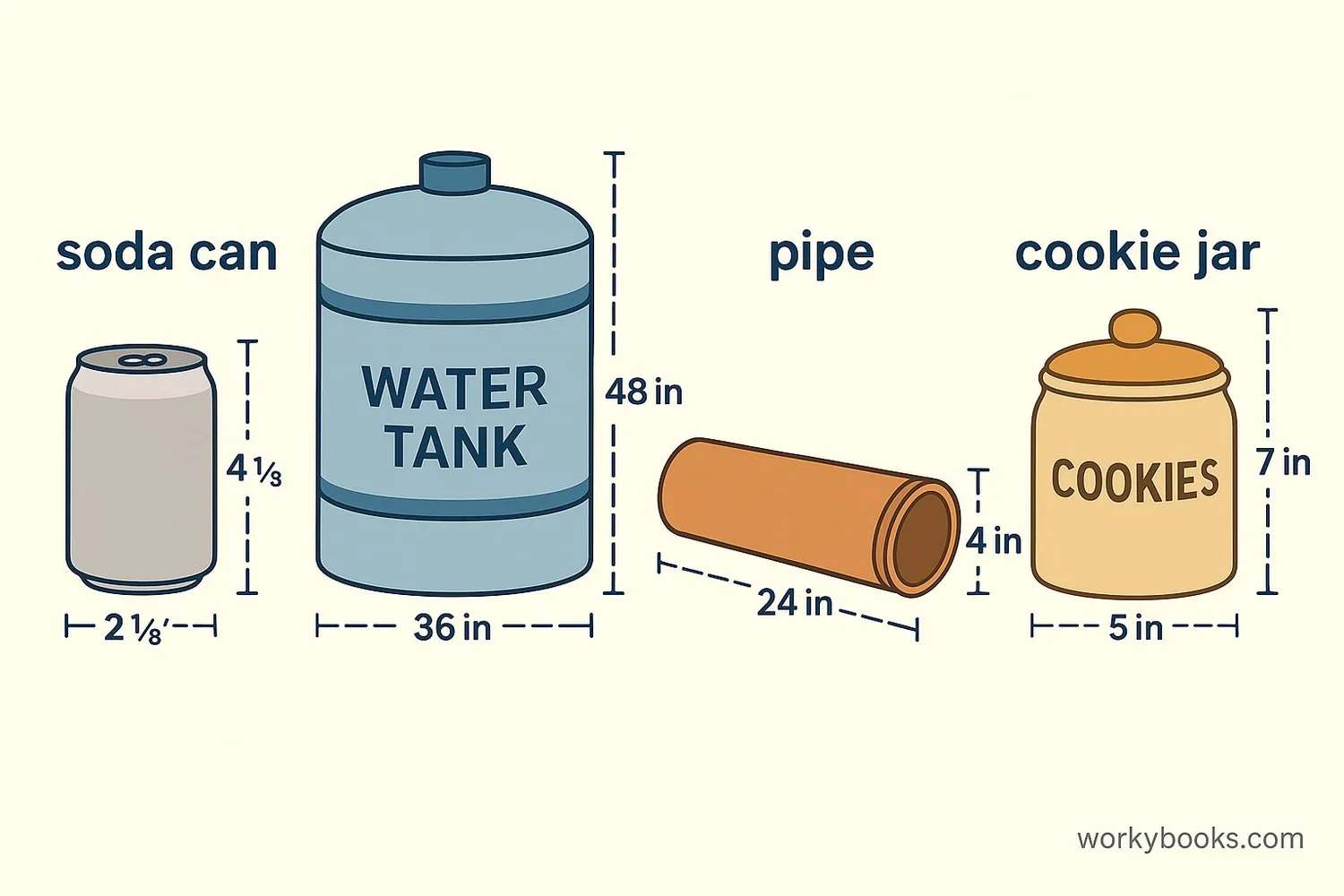
Let's calculate volume for some real objects:
Example 1: Soda Can
V = πr²h = 3.14 × (3.3)² × 12 ≈ 410 cm³
That's about 410 ml (since 1 cm³ = 1 ml)
V = πr²h = 3.14 × (1)² × 3 ≈ 9.42 m³
That's 9,420 liters of water!
V = πh(R² - r²) = 3.14 × 200 × (10² - 8²)
V = 3.14 × 200 × (100 - 64) = 3.14 × 200 × 36 ≈ 22,608 cm³
Measurement Tip
1 cm³ = 1 milliliter, and 1000 cm³ = 1 liter. Use this to convert between volume and capacity.
Volume Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about cylinder volume:
Math Trivia
Discover interesting facts about cylinders and volume:
Ancient Measurement
The ancient Egyptians used cylinder volume calculations to measure grain storage in silos over 4,000 years ago. Their methods were surprisingly accurate!
Water Tower Capacity
The world's largest water tower is in Kuwait. It holds over 9,000 cubic meters of water - that's enough to fill 3.6 Olympic swimming pools!
Rocket Fuel
NASA engineers use cylinder volume calculations to determine how much fuel fits in rocket boosters. A single Space Shuttle booster held over 500,000 gallons of fuel!
Tallest Cylinder
The tallest cylindrical structure is the KVLY-TV mast in North Dakota, standing at 629 meters (2,063 ft) tall. That's taller than the Empire State Building!


