Volume of Cylinder - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate the space inside cylinders with easy explanations, examples, and practice activities
What is Volume of a Cylinder?
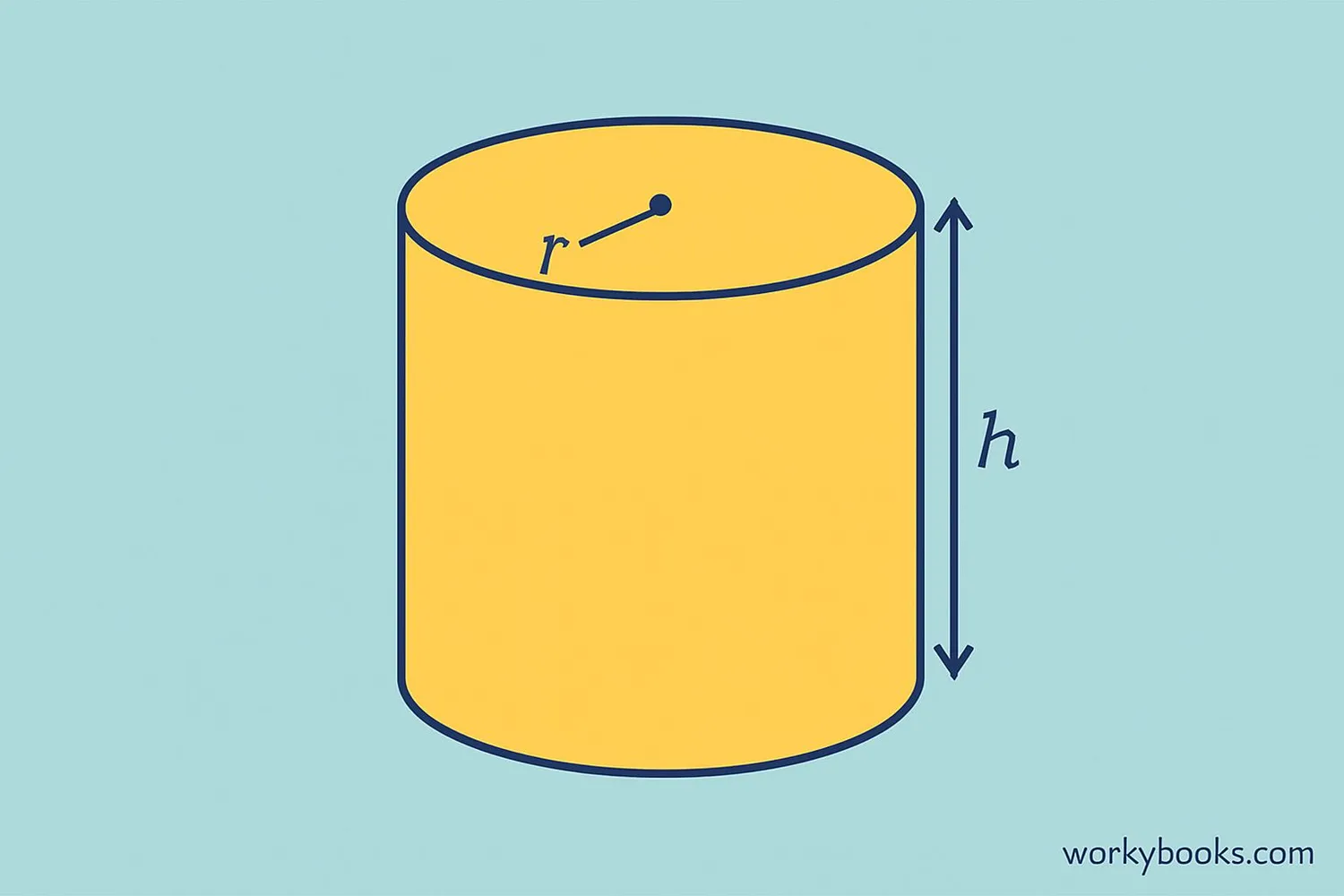
The volume of a cylinder tells us how much space is inside it. Imagine filling a can with water - the volume would be how much water it can hold.
A cylinder is a 3D shape with:
- Two identical circular bases (like the top and bottom of a can)
- A curved surface connecting the bases
- A height (h) - the distance between the bases
- A radius (r) - the distance from the center to the edge of the base
Volume is measured in cubic units like cm³, m³, or liters. Understanding volume helps us solve real problems like:
• How much juice fits in a bottle
• The amount of water in a pipe
• The capacity of storage tanks
Key Concept
Volume measures the space inside a 3D object. For cylinders, we calculate it using the base area and height.
Volume of Cylinder Formula

To calculate a cylinder's volume, we use this formula:
Volume Formula
Where:
V = Volume
π ≈ 3.14 (Pi)
r = radius of the base
h = height of the cylinder
1. πr² calculates the area of the circular base
2. × h multiplies the base area by height to get volume
Example: For a cylinder with radius 3 cm and height 5 cm:
Step 1: Calculate base area → π × 3² ≈ 3.14 × 9 ≈ 28.26 cm²
Step 2: Multiply by height → 28.26 × 5 ≈ 141.3 cm³
So the volume is about 141.3 cubic centimeters.
Remember
Always square the radius first (r²), then multiply by π, then by height. Keep units consistent (all cm or all m).
Real-World Examples

Let's practice with real-world cylinder volumes:
Example 1: A soda can has radius 3.1 cm and height 12 cm. What's its volume?
Solution: V = π × (3.1)² × 12 ≈ 3.14 × 9.61 × 12 ≈ 362 cm³ (or 362 ml)
Example 2: A water tank has diameter 2m (so radius 1m) and height 5m. Calculate its volume in liters.
Solution: V = π × (1)² × 5 ≈ 15.7 m³ = 15,700 liters (since 1m³ = 1000L)
Example 3: Find the volume of a pencil with radius 0.4 cm and length 18 cm.
Solution: V = π × (0.4)² × 18 ≈ 3.14 × 0.16 × 18 ≈ 9 cm³
Example 4: A cylindrical glass holds 500ml (500cm³) when full. If its radius is 4cm, how tall is it?
Solution: Rearrange formula: h = V ÷ (πr²) = 500 ÷ (3.14 × 16) ≈ 9.95 cm
Try measuring cylindrical objects around you and calculate their volumes!
Conversion Tip
1 milliliter (mL) = 1 cubic centimeter (cm³). For liters: 1000 cm³ = 1 liter.
Volume of Cylinder Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about cylinder volume:
Math Trivia
Discover interesting facts about cylinders and measurement:
Ancient Measurements
The ancient Egyptians used cylindrical grain silos over 4,000 years ago. They developed early volume calculations to track food supplies, though their methods were different from ours today.
Water Towers
Most water towers are cylindrical because this shape provides the strongest structure for holding large volumes of water while using the least material. A typical water tower holds about 1 million gallons!
Rocket Fuel
Space rockets use cylindrical fuel tanks because cylinders can hold large volumes efficiently. The Saturn V rocket's first stage held over 2 million liters of fuel in cylindrical tanks.
Largest Cylinder
The world's largest cylindrical aquarium is in Berlin, holding 1 million liters of water. It's 25 meters tall with a diameter of 11 meters - that's a volume of about π × (5.5)² × 25 ≈ 2,375 cubic meters!


