Algebraic Identities - Definition, Examples, Quiz, FAQ, Trivia
Learn essential math formulas with clear explanations, examples, and practice activities
What are Algebraic Identities?
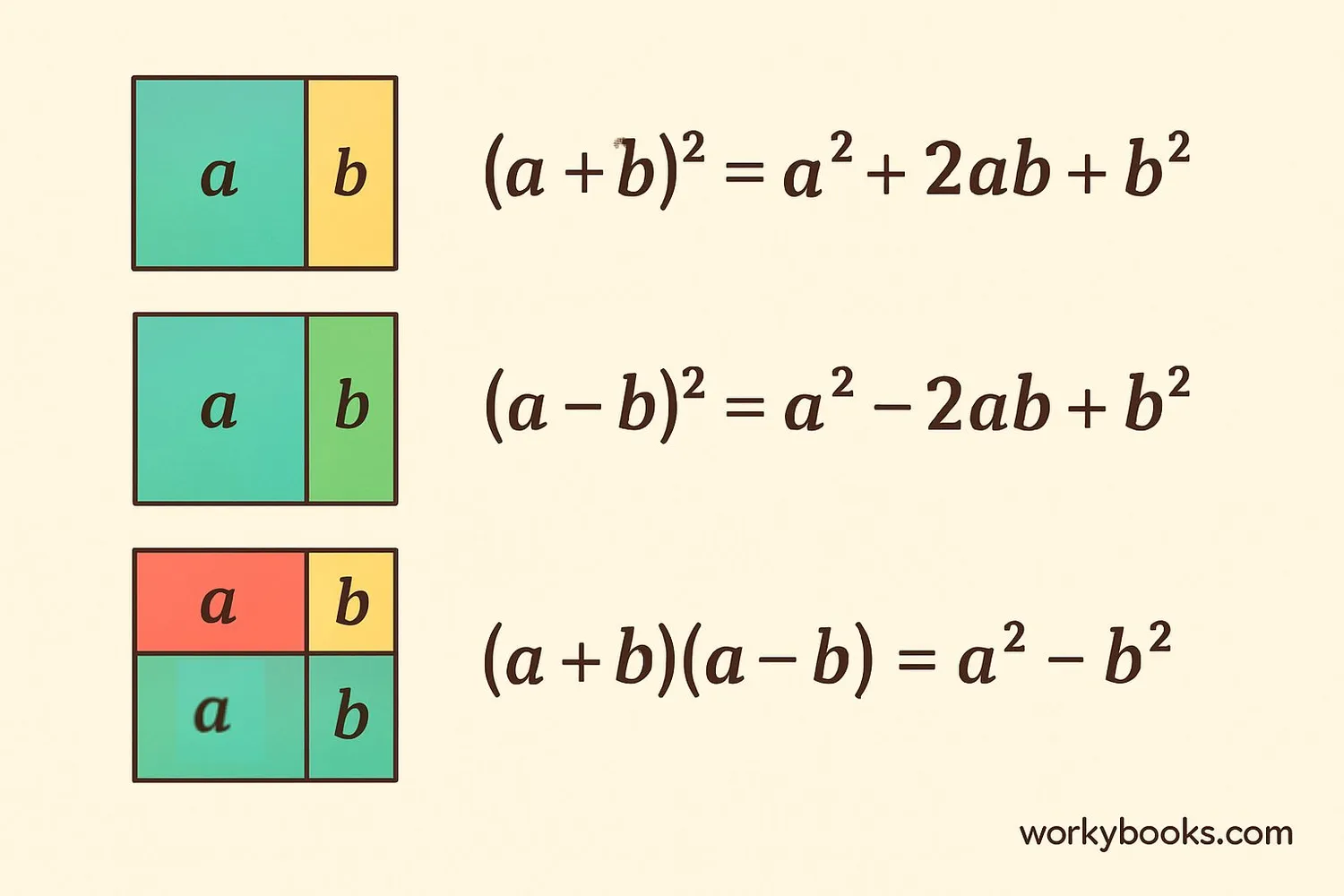
Algebraic identities are special equations that are always true for all values of the variables. They're like mathematical shortcuts that help us solve problems faster and simplify complex expressions.
Think of them as reliable friends in math - they always work no matter what numbers you use! These identities save us time because we don't have to do the same calculations repeatedly.
Algebraic identities are especially useful for:
- Simplifying complex expressions
- Solving equations more quickly
- Factoring polynomials
- Expanding expressions
Key Concept
Algebraic identities are equations that hold true for all values of the variables they contain.
Basic Algebraic Identities
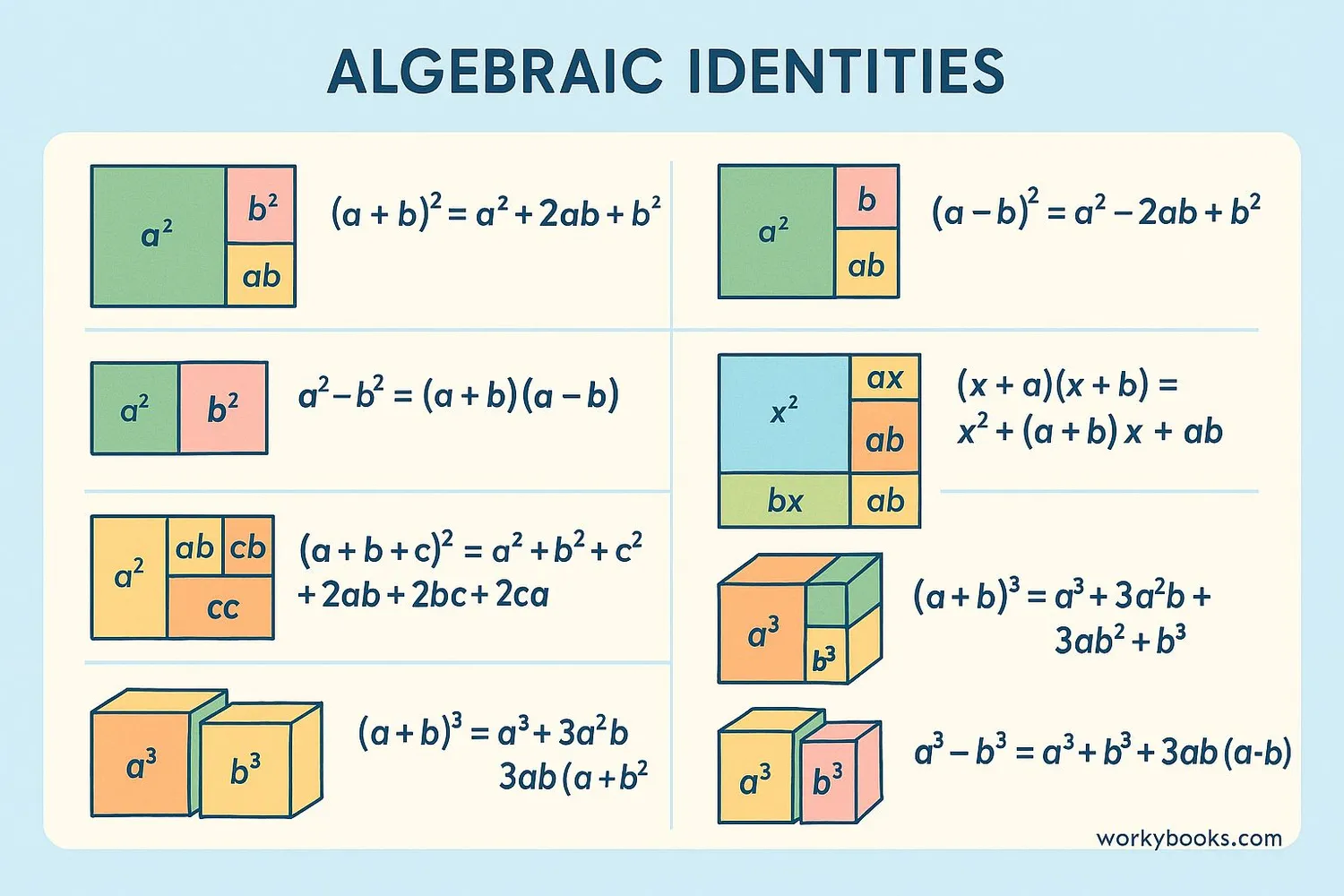
Here are the most important algebraic identities you should know. These form the foundation for more complex algebraic work:
Square of a Sum
When you square a sum of two terms, it equals the sum of the squares plus twice their product.
Square of a Difference
When you square a difference of two terms, it equals the sum of the squares minus twice their product.
Difference of Squares
The difference between two squares factors into the product of their sum and difference.
Product of Binomials
When multiplying two binomials with the same first term, the result is a quadratic expression.
Cube of a Sum
The cube of a sum expands to the sum of cubes plus three times the products of squares and terms.
Cube of a Difference
The cube of a difference expands similarly to the sum but with alternating signs.
Sum of Cubes
The sum of two cubes factors into a binomial and a trinomial expression.
Difference of Cubes
The difference of two cubes factors similarly to the sum but with sign differences.
Remember
These identities work for any values of a and b. Try plugging in numbers to verify them yourself!
Examples of Algebraic Identities
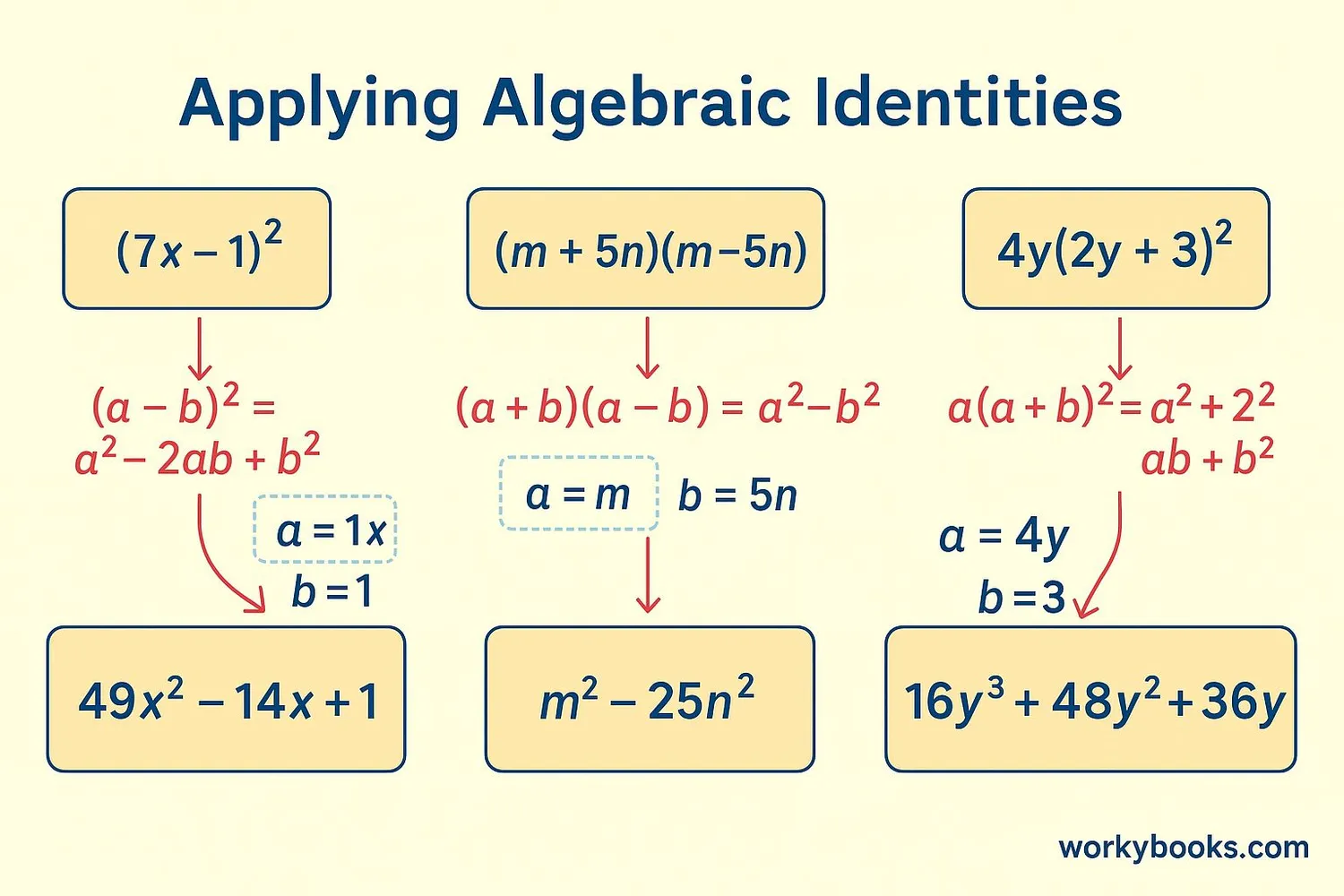
Let's see how these identities work with numbers. We'll work through some examples step by step:
Example 1: Using (a + b)²
Expand (3 + 4)² using the identity
Solution: (3 + 4)² = 3² + 2×3×4 + 4² = 9 + 24 + 16 = 49
Example 2: Using a² - b²
Factorize 25x² - 16
Solution: 25x² - 16 = (5x)² - 4² = (5x + 4)(5x - 4)
Example 3: Using (x + a)(x + b)
Expand (x + 3)(x + 5)
Solution: (x + 3)(x + 5) = x² + (3+5)x + (3×5) = x² + 8x + 15
Example 4: Using (a - b)³
Expand (2x - 1)³
Solution: (2x - 1)³ = (2x)³ - 3×(2x)²×1 + 3×(2x)×1² - 1³ = 8x³ - 12x² + 6x - 1
Practice Tip
Try creating your own examples by choosing different values for a and b. This helps you understand how identities work.
Algebraic Identities Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about algebraic identities:
Math Trivia
Discover interesting facts about algebra and mathematics:
Origin of Algebra
The word "algebra" comes from the Arabic word "al-jabr" which means "reunion of broken parts." It was first used by the Persian mathematician Muhammad ibn Musa al-Khwarizmi in the 9th century.
Algebraic Symbolism
The use of letters to represent unknowns in equations was developed by French mathematician François Viète in the 16th century. Before this, mathematicians used words to describe equations.
Algebra in Space
Algebraic identities are fundamental to space travel calculations. NASA engineers use them to calculate trajectories, orbital mechanics, and spacecraft design parameters.
Mental Math Records
Many mental math champions use algebraic identities to perform complex calculations quickly. The identity a² - b² = (a+b)(a-b) is especially useful for calculating differences of large squares mentally.





