Alternate Exterior Angles - Definition, Examples, Facts & Quiz, FAQ, Trivia
Learn about angle relationships with easy explanations, visual examples, and interactive activities
What are Alternate Exterior Angles?
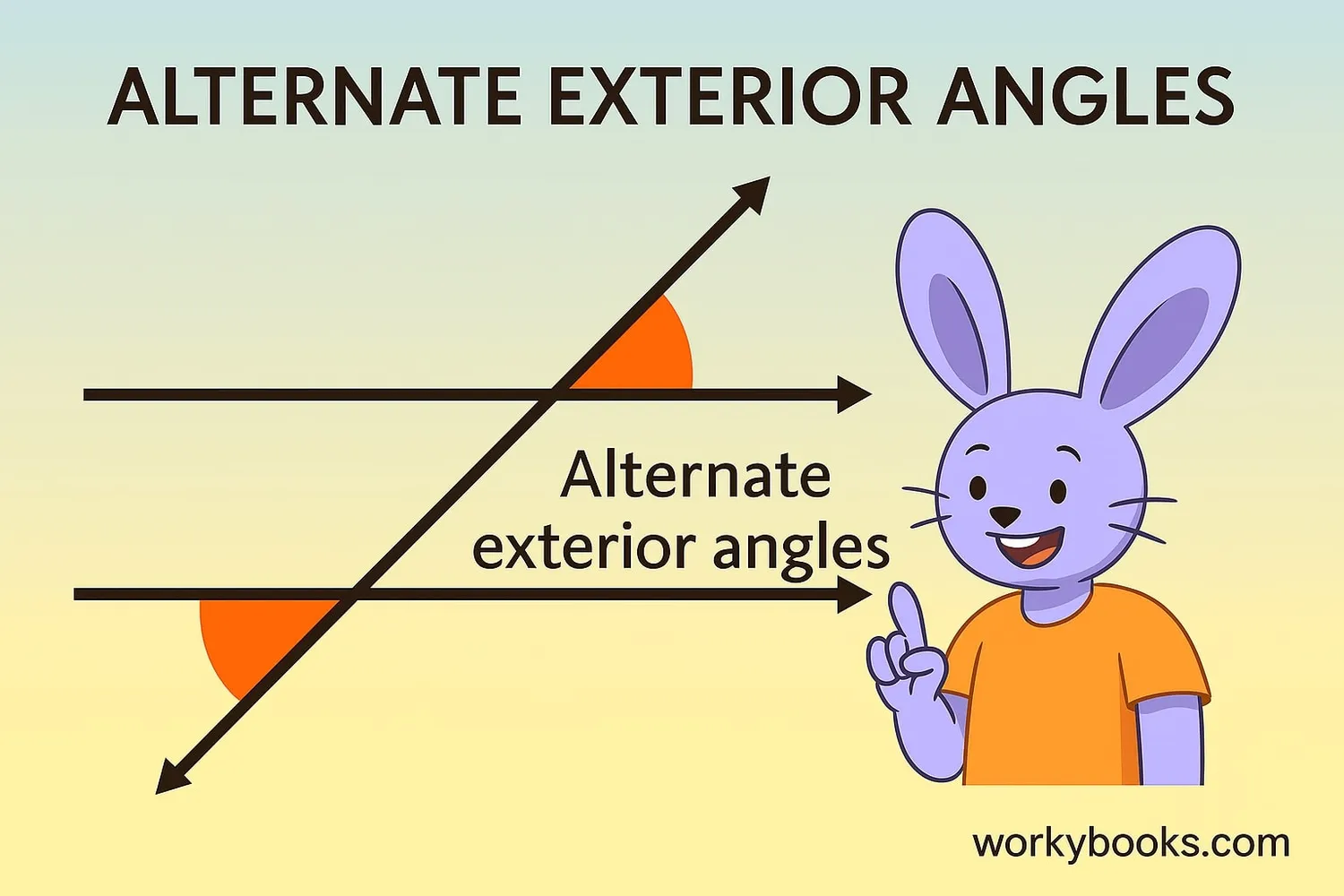
Alternate exterior angles are pairs of angles that are:
1. Outside the two parallel lines
2. On opposite sides of the transversal
3. Not adjacent to each other
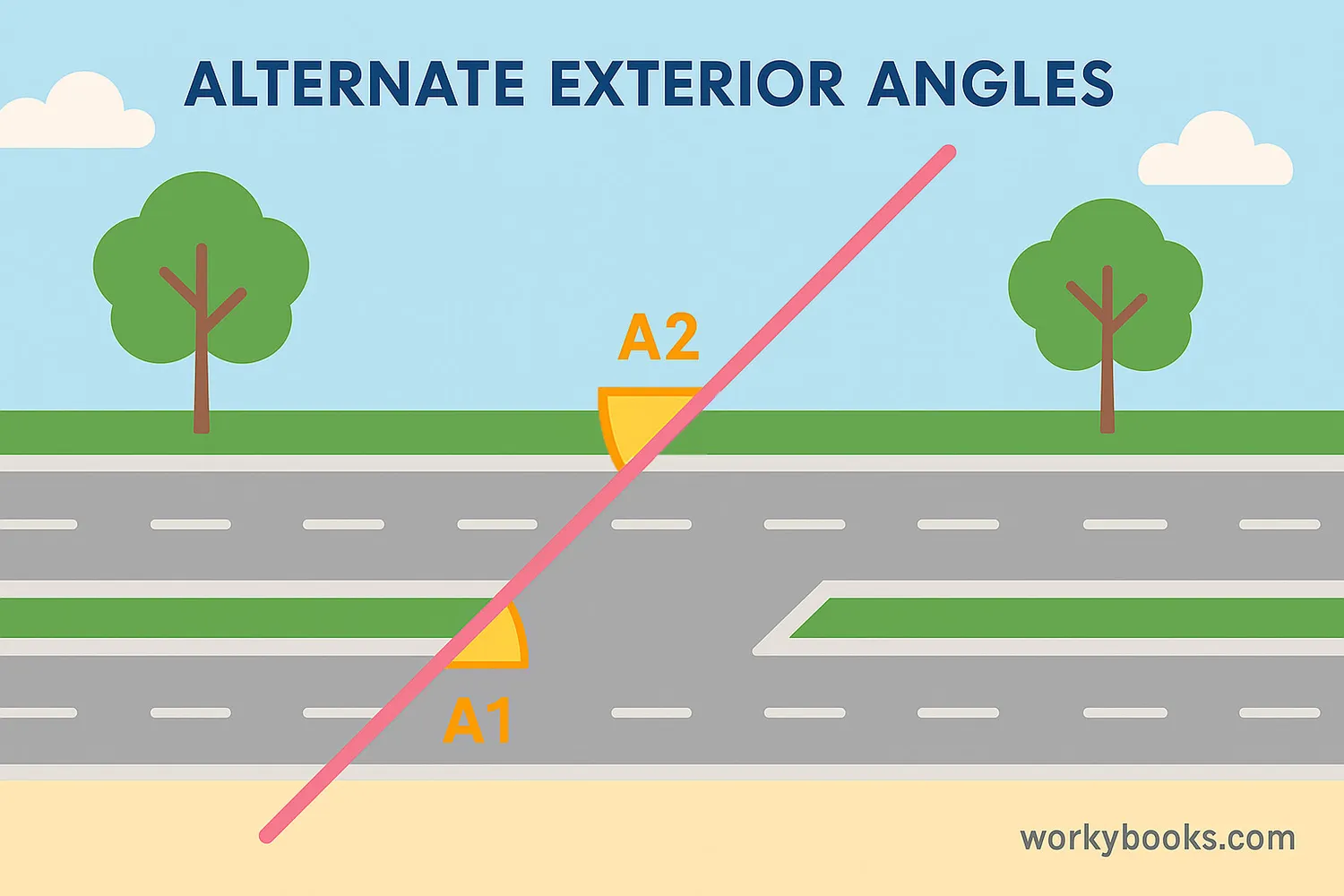
When two parallel lines are cut by a transversal (a line that crosses both parallel lines), eight angles are formed. The alternate exterior angles are the angles that are on the outer side of the parallel lines and on opposite sides of the transversal.
In the diagram above, angles 1 and 7 are alternate exterior angles, and angles 2 and 8 are also alternate exterior angles.
Key Concept
Alternate exterior angles are found when you have two parallel lines and a transversal crossing them.
Alternate Exterior Angles Theorem
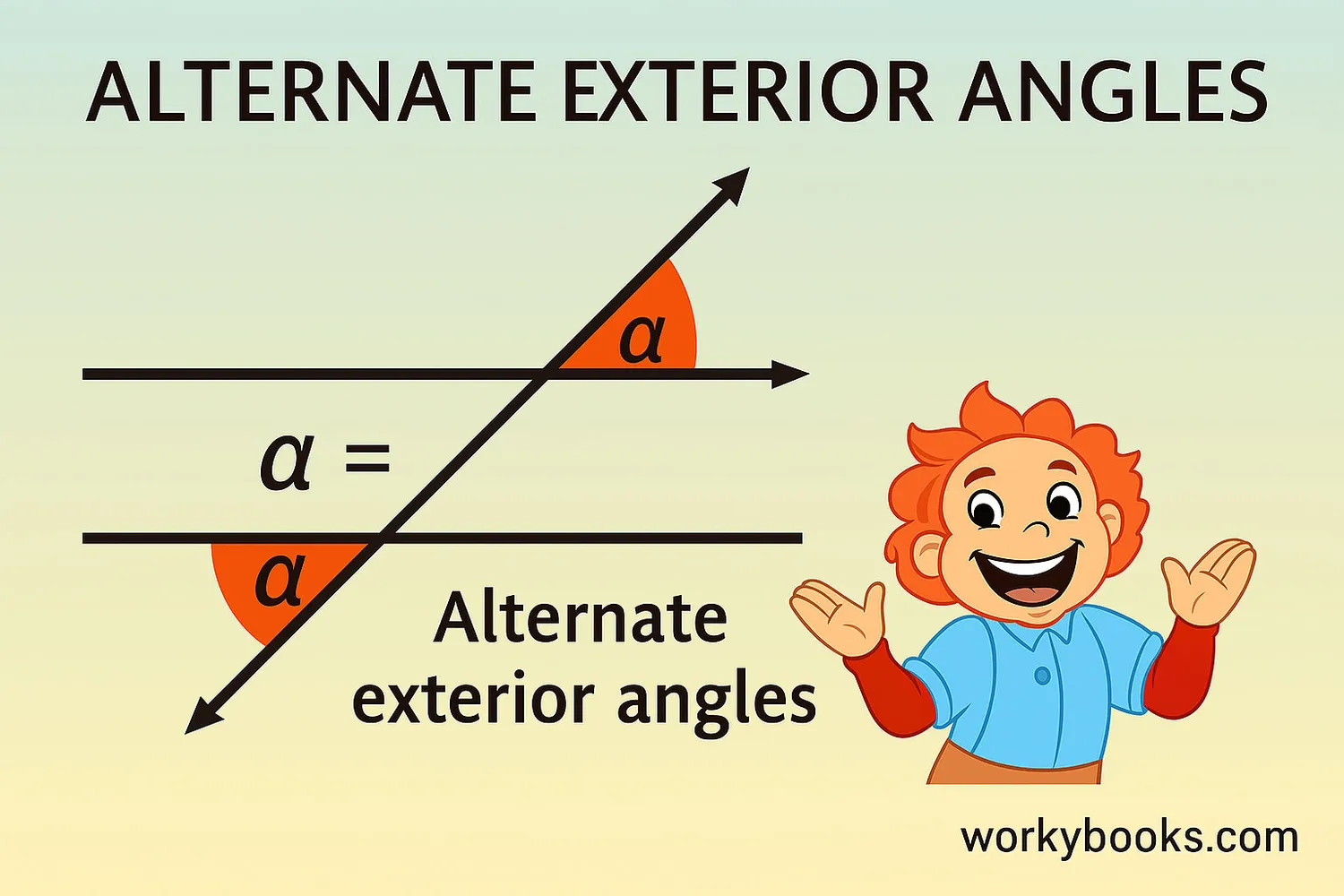
The Alternate Exterior Angles Theorem states:
Theorem Statement
If two parallel lines are cut by a transversal, then each pair of alternate exterior angles is equal.
Why is this important? This theorem helps us solve geometry problems without measuring every angle. If we know one alternate exterior angle, we automatically know its pair!
Remember
The theorem only works when the lines are parallel. If the lines aren't parallel, the alternate exterior angles won't be equal.
Proof of the Alternate Exterior Angles Theorem
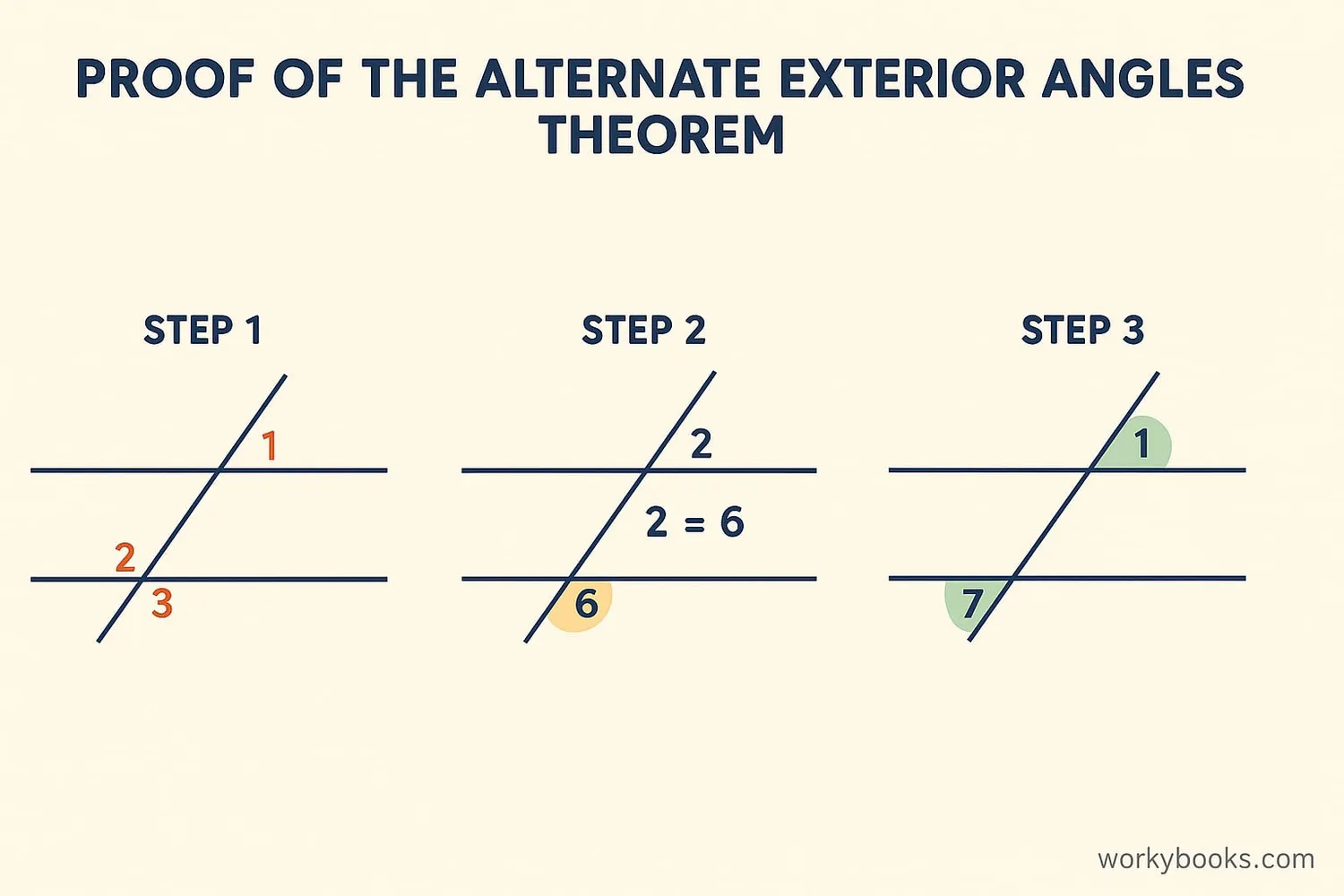
Let's prove why alternate exterior angles are equal when lines are parallel:
Step 1: Consider two parallel lines cut by a transversal.
Step 2: We know that corresponding angles are equal (Corresponding Angles Postulate).
Step 3: Notice that one alternate exterior angle (like angle 1) corresponds to the other alternate exterior angle (like angle 7).
Step 4: Since corresponding angles are equal, and these are corresponding angles, they must be equal.
Therefore, we've proved that alternate exterior angles are equal when lines are parallel!
Proof Tip
Remember that the proof depends on the Corresponding Angles Postulate. This is why corresponding angles are so important in geometry!
Are Alternate Exterior Angles Congruent?
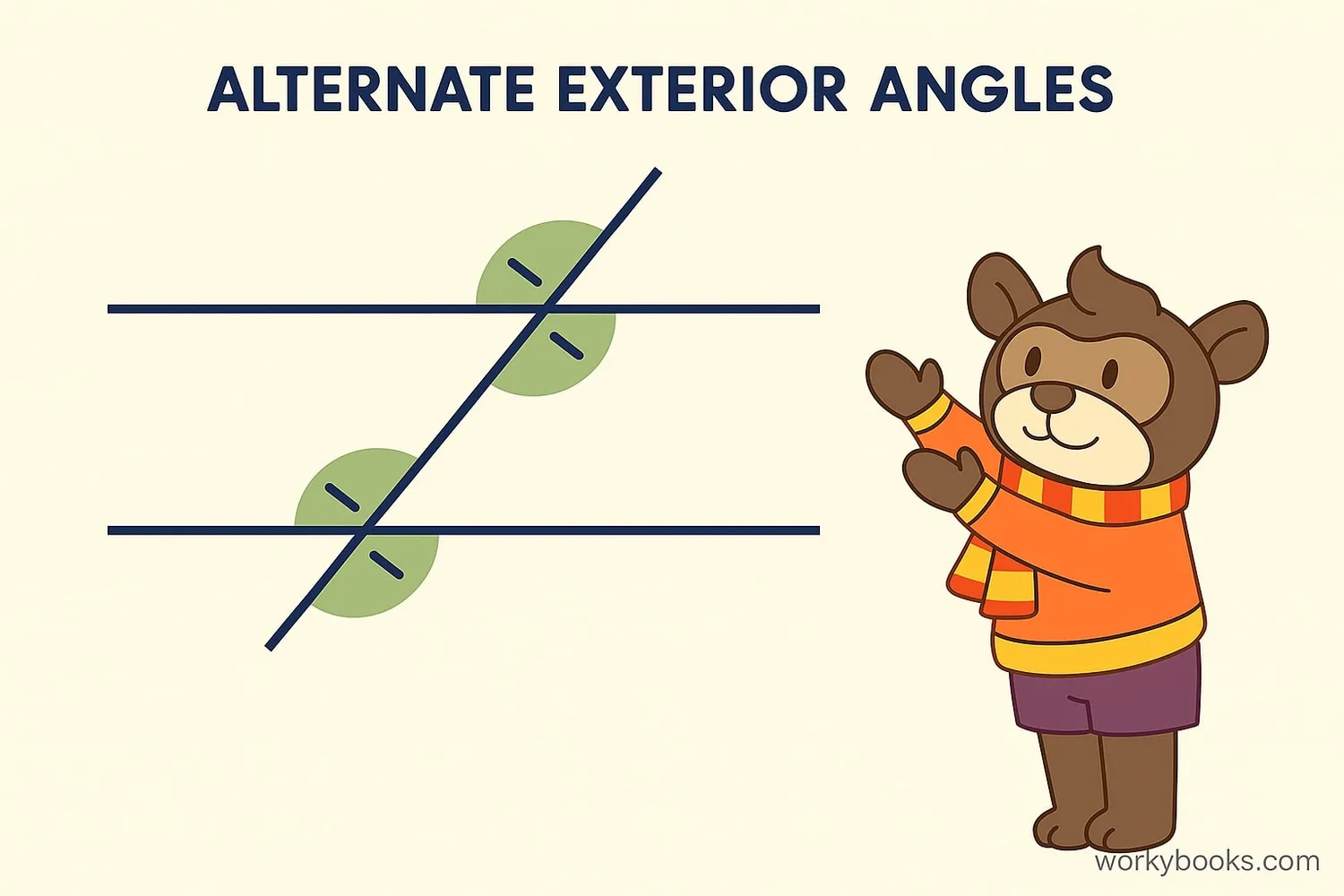
Yes! When two parallel lines are cut by a transversal, the alternate exterior angles are always congruent. This means they have exactly the same measurement.
For example:
If angle 1 measures 120°, then angle 7 (its alternate exterior pair) will also measure 120°.
If angle 2 measures 60°, then angle 8 will also measure 60°.
This congruence is what makes alternate exterior angles so useful in geometry problems. We can use this relationship to find missing angle measurements without using a protractor.
Important Note
Alternate exterior angles are only congruent when the lines are parallel. If the lines aren't parallel, this relationship doesn't hold true.
Real-World Examples
Alternate exterior angles aren't just for textbooks! You can find them in the world around you:
1. Railroad Tracks: The tracks are parallel lines, and the wooden ties are transversals. The angles formed at the intersection create alternate exterior angles.
2. Window Grills: Many windows have parallel bars with diagonal supports forming transversals.
3. Bridge Structures: Engineers use parallel beams with diagonal supports, creating many pairs of angles.
4. Book Shelves: The shelves are parallel, and the side supports act as transversals.
Next time you're outside, look for parallel lines crossed by another line - you'll see geometry in action!
Observation Tip
Look for structures with repeating parallel patterns - they often contain many examples of alternate exterior angles.
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about alternate exterior angles:
Geometry Trivia
Discover interesting facts about angles and geometry:
Ancient Angle Knowledge
The ancient Egyptians used angle relationships when building the pyramids around 2500 BC. They understood practical geometry even before formal mathematical proofs existed.
Nature's Angles
Honeybees build their hives with hexagonal cells that form precise 120° angles. This efficient design uses the least amount of wax while creating strong structures.
Angles in Space
Astronomers use angles to measure distances between stars. The concept of parallax angle helps determine how far away stars are from Earth.
Angle World Record
The most precise angle ever measured was in a scientific experiment where researchers measured an angle to within 0.0000000001 degrees - that's incredibly precise!





