Square Root of 200 - Definition, Examples, Quiz, FAQ, Trivia
Learn what square roots are and how to find the square root of 200 with different methods
What is Square Root?
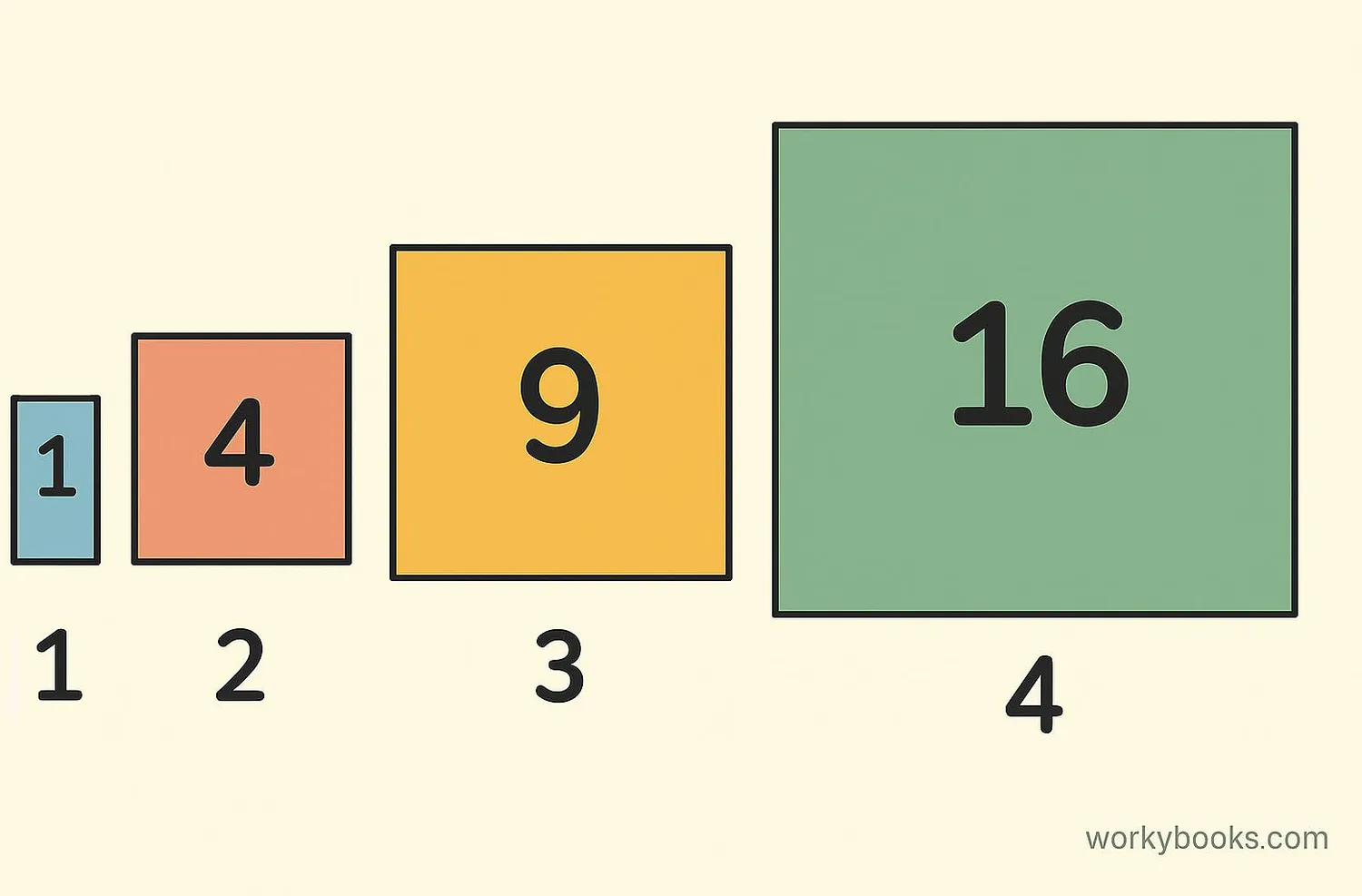
A square root of a number is a value that, when multiplied by itself, gives the original number. The square root symbol is called the radical symbol (√).
For example:
√9 = 3 because 3 × 3 = 9
√16 = 4 because 4 × 4 = 16
Numbers like 9 and 16 are called perfect squares because their square roots are whole numbers. The number 200 is not a perfect square, but we can still find its square root.
Square Root Definition
This means y is the square root of x because y multiplied by itself equals x.
Key Concept
The square root of 200 is approximately 14.1421. This is an irrational number, meaning its decimal form never ends and never repeats.
Methods to Find √200

There are several ways to find the square root of 200. Let's look at three methods:
1. Prime Factorization Method
Step 1: Break down 200 into prime factors:
200 = 2 × 2 × 2 × 5 × 5
Step 2: Pair the prime factors:
(2 × 2) and (5 × 5) with one 2 left unpaired
Step 3: Take one number from each pair:
2 × 5 = 10
Step 4: Multiply by the square root of the unpaired factor:
√200 = 10 × √2 ≈ 10 × 1.4142 ≈ 14.1421
2. Long Division Method
This method involves dividing the number in steps:
1. Group digits in pairs from the decimal point
2. Find the largest number whose square is ≤ the first pair
3. Subtract and bring down the next pair
4. Double the quotient and find the next digit
5. Repeat until you reach desired precision
Following these steps gives us √200 ≈ 14.1421
3. Estimation Method
We know that:
14² = 196
15² = 225
Since 200 is between 196 and 225, √200 is between 14 and 15.
The difference is 200 - 196 = 4
Total difference is 225 - 196 = 29
So √200 ≈ 14 + (4/29) ≈ 14.1379
This is close to the actual value of ≈14.1421
Remember
The square root of 200 is irrational, so we usually write it as √200 or approximate it as 14.14.
Examples with √200
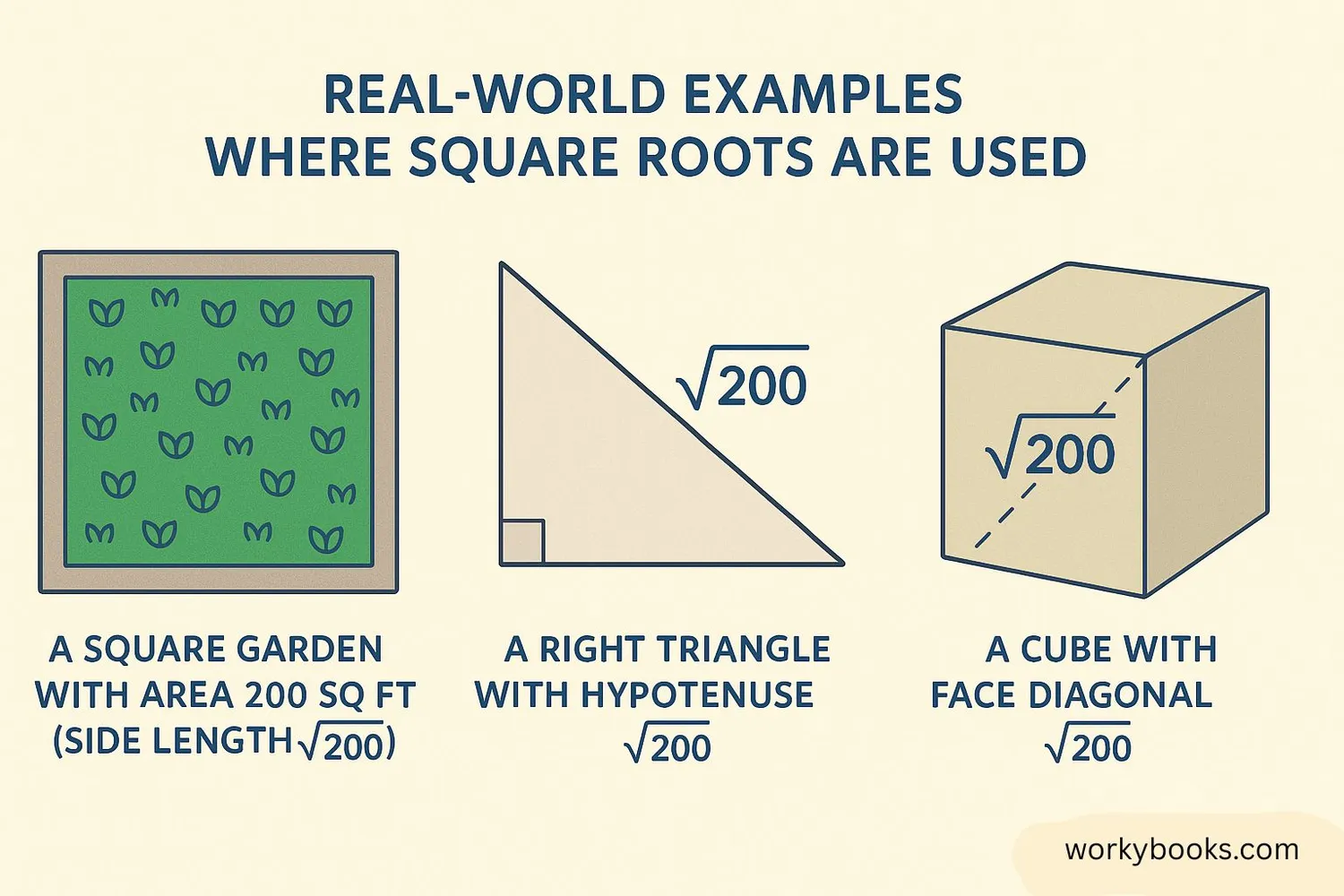
Let's see how √200 appears in different situations:
Example 1: A square garden has an area of 200 square feet. How long is each side?
Solution: Side length = √200 ≈ 14.14 feet
Example 2: In a right triangle, if the two shorter sides are 10 and 10, what is the hypotenuse?
Solution: Hypotenuse = √(10² + 10²) = √200 ≈ 14.14 units
Example 3: The diagonal of a square is 20 cm. What is the length of each side?
Solution: Diagonal = side × √2 → side = 20/√2 = 10√2 ≈ 14.14 cm
Example 4: Simplify 3√200
Solution: 3√200 = 3 × √(100×2) = 3 × 10√2 = 30√2 ≈ 42.4264
Simplification Tip
√200 can be simplified to 10√2 because 200 = 100 × 2, and √100 = 10.
Square Root Quiz
Test your understanding of square roots with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about square roots:
Math Trivia
Discover interesting facts about square roots and numbers:
Ancient Square Roots
The Babylonians had methods for finding square roots as early as 2000 BCE! They used a form of the estimation method similar to what we use today.
Irrational Discovery
The ancient Greeks were shocked to discover irrational numbers like √2. According to legend, the mathematician who proved √2 was irrational was drowned for revealing this "heresy."
Square Roots in Space
NASA uses square roots in rocket trajectory calculations. The distance between two points in space is calculated using a 3D version of the Pythagorean theorem involving square roots.
Square Root Records
The world record for calculating the most digits of √2 is over 10 trillion digits! The calculation took 94 days using a powerful computer.





