Square Root of 20 - Definition, Examples, Quiz, FAQ, Trivia
Learn how to find square roots with easy explanations, visual examples, and practice activities
What is Square Root?

A square root is a number that, when multiplied by itself, gives the original number. It's the opposite of squaring a number. The square root symbol is called the radical symbol (√).
For example:
• The square root of 4 is 2 because 2 × 2 = 4
• The square root of 9 is 3 because 3 × 3 = 9
• The square root of 16 is 4 because 4 × 4 = 16
Numbers that have whole number square roots are called perfect squares. Numbers like 20 that don't have whole number square roots are called imperfect squares.
Square Root Formula
This means that b multiplied by itself equals a
Key Concept
The square root operation answers the question: "What number multiplied by itself gives this result?"
Square Root of 20
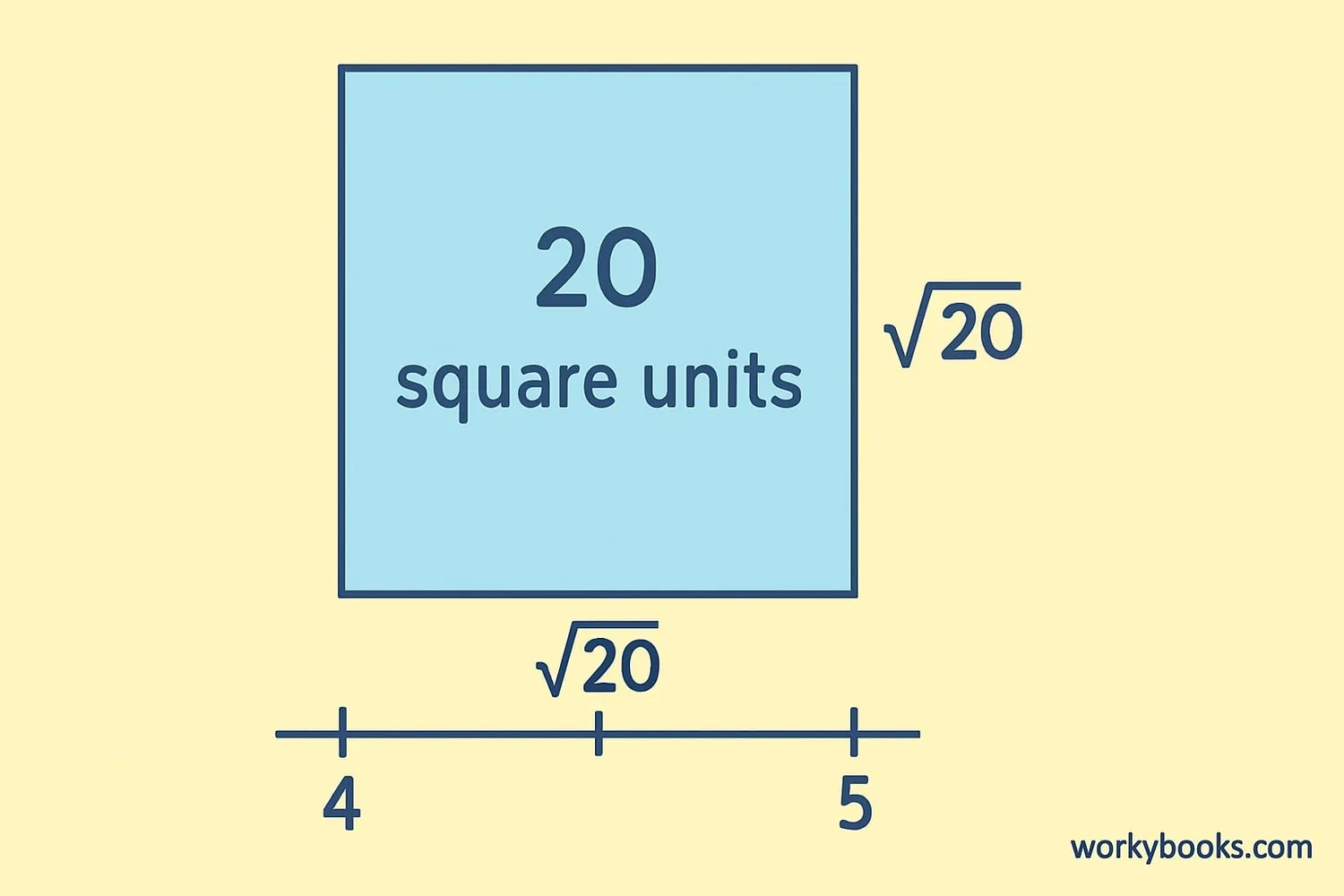
The square root of 20 is written as √20. Since 20 is not a perfect square, √20 is not a whole number. It's approximately 4.472.
We know this because:
• 4 × 4 = 16 (which is less than 20)
• 5 × 5 = 25 (which is greater than 20)
So √20 must be between 4 and 5. Using calculation methods, we find it's approximately 4.472.
Approximation
4.472 × 4.472 = 20.000 (approximately)
Remember
Every positive number has two square roots - a positive and a negative. For √20, we have +4.472 and -4.472.
Methods to Find Square Root of 20
There are several ways to find the square root of a number. Let's look at three methods for finding √20:
1. Prime Factorization Method
2. Long Division Method
3. Repeated Subtraction Method
Method Tip
The long division method is most precise for finding decimal values of square roots, while prime factorization is great for simplifying radicals.
Is √20 Rational or Irrational?

The square root of 20 is an irrational number. Here's why:
• A rational number can be expressed as a fraction a/b where a and b are integers
• √20 = 2√5, and √5 is irrational (it cannot be expressed as a simple fraction)
• The decimal expansion of √20 is non-terminating and non-repeating: 4.472135954999579...
Since √20 cannot be expressed as a simple fraction and its decimal goes on forever without repeating, it is irrational.
Rational vs. Irrational
Non-terminating, non-repeating decimal → Irrational
Key Concept
Square roots of non-perfect squares are always irrational numbers. Since 20 is not a perfect square, √20 is irrational.
Square Root Quiz
Test your understanding of square roots with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about square roots:
Math Trivia
Discover interesting facts about square roots and mathematics:
Ancient Square Roots
The Babylonians calculated square roots as early as 2000 BCE using a method similar to long division. They had clay tablets showing √2 accurate to six decimal places!
Golden Ratio
The golden ratio (approximately 1.618) involves square roots in its calculation: (1 + √5)/2. This ratio appears in nature, art, and architecture.
Radical Symbol Origin
The radical symbol (√) was first used by Christoph Rudolff in 1525. It may have evolved from the letter "r" for "radix" (Latin for root), or from a dot with an upward stroke.
Square Root Records
The most decimal places of √20 ever calculated is over 10 trillion digits! In 2021, a Swiss university calculated √20 to 10,000,000,000,000 decimal places.





