Square Root of 169 - Definition, Examples, Quiz, FAQ, Trivia
Learn what √169 means and how to calculate it with easy explanations and practice activities
What is Square Root?
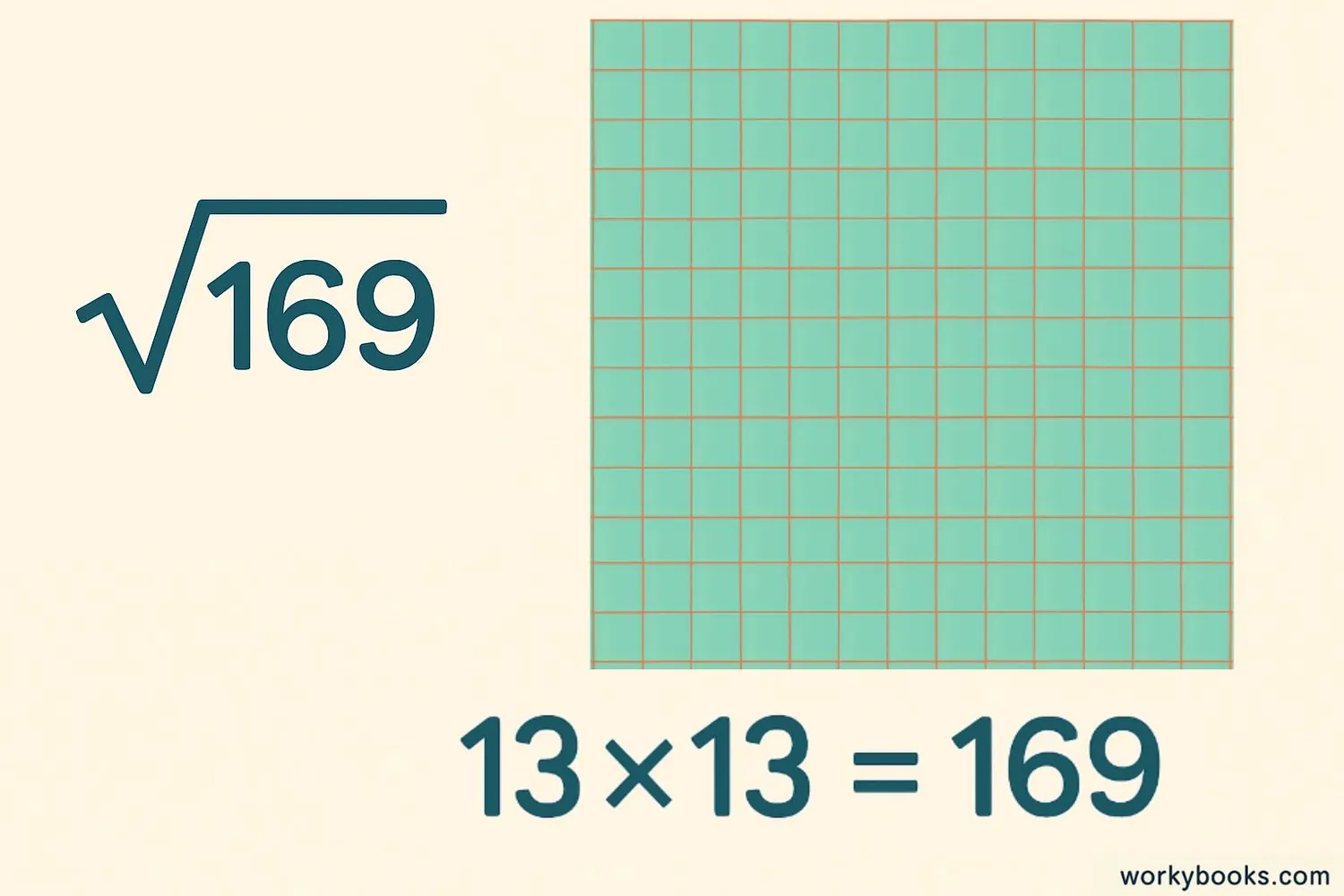
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 169 is 13 because 13 × 13 = 169.
The square root symbol is called the radical symbol (√). The number inside the radical symbol is called the radicand. So in √169, 169 is the radicand.
Every positive number has two square roots: a positive and a negative. For 169, the square roots are 13 and -13 because both 13×13 and (-13)×(-13) equal 169. The positive square root is called the principal square root.
because
13 × 13 = 169
Key Concept
Square roots are the opposite of squaring a number. If 13² = 169, then √169 = 13.
How to Find the Square Root of 169

Finding the square root of 169 is straightforward because 169 is a perfect square (a number that is the square of an integer).
Here's how to find it:
Square Root Formula
We need to find the number that when multiplied by itself equals 169.
10 × 10 = 100 (too small)
11 × 11 = 121 (too small)
12 × 12 = 144 (too small)
13 × 13 = 169 (perfect!)
14 × 14 = 196 (too big)
So the square root of 169 is 13.
Remember
Perfect squares like 169 have whole number square roots. Numbers that aren't perfect squares have decimal square roots.
Methods to Find the Square Root
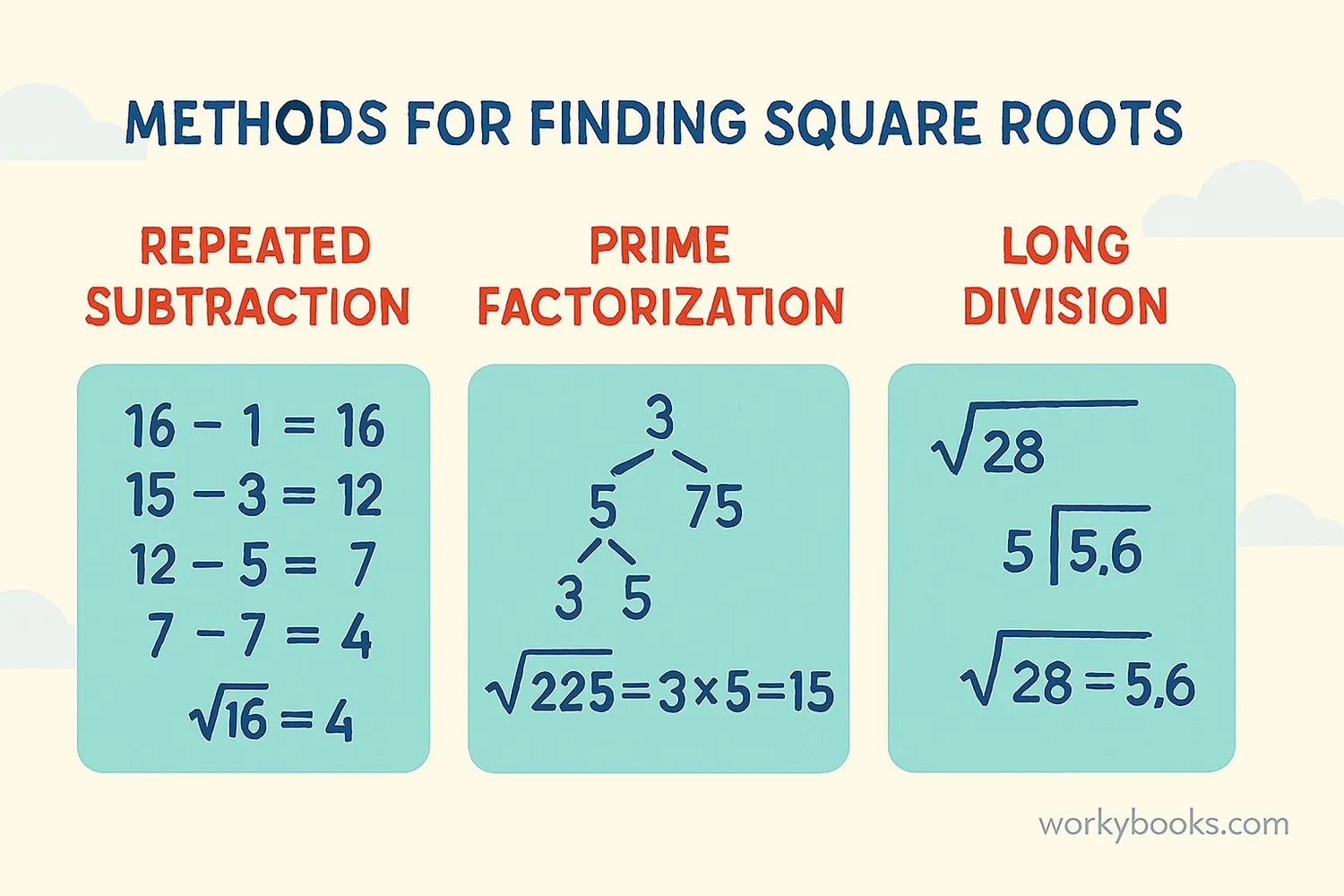
1. Repeated Subtraction Method
- Start with 169
- Subtract consecutive odd numbers: 1, 3, 5, 7...
- Count how many subtractions until you reach zero
- That count is the square root
168 - 3 = 165
165 - 5 = 160
... continue subtracting ...
After 13 subtractions, we reach 0
∴ √169 = 13
2. Prime Factorization Method
- Factor 169 into prime factors
- 169 = 13 × 13
- Group identical factors in pairs
- Take one factor from each pair
- Multiply these factors together
√169 = √(13 × 13) = 13
3. Long Division Method
- Place a bar over the number 169
- Find the largest number whose square is ≤ 1 (which is 1)
- Subtract and bring down the next pair (69)
- Double the quotient (1 becomes 2) and find a digit (X) such that (20 + X) × X ≤ 69
- 3 fits: (20 + 3) × 3 = 69
- Subtract and get remainder 0
1 3
√1 69
-1
-----
0 69
- 69
-----
0
Method Tip
Prime factorization is easiest for perfect squares like 169. Use long division for numbers that aren't perfect squares.
Is √169 Rational or Irrational?

The square root of 169 is a rational number because it can be expressed as a simple fraction.
Why?
• 13 is a whole number
• It can be written as 13/1 (a ratio of two integers)
• Its decimal representation (13.0) terminates
In contrast, an irrational number cannot be expressed as a simple fraction and has a decimal that goes on forever without repeating. Examples include √2 (≈1.414213...) and π (≈3.14159...).
Since 169 is a perfect square (13² = 169), its square root is always rational.
Important Note
All perfect squares have rational square roots. Numbers that aren't perfect squares have irrational square roots.
Square Root Practice Quiz
Test your understanding of square roots with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about square roots:
Math Trivia
Discover interesting facts about square roots and mathematics:
Ancient Square Roots
The concept of square roots dates back to ancient Babylon around 1800 BCE. Babylonian mathematicians calculated square roots using geometric methods on clay tablets.
Radical Symbol Origin
The radical symbol (√) was first used in 1525 by mathematician Christoph Rudolff. It comes from the letter "r" for "radix" (Latin for "root"). The horizontal bar was added later to show how much of the expression is under the radical.
Square Root Day
Square Root Day is celebrated when both the day and month are the square root of the last two digits of the year. For example: 4/4/16 (√16=4) or 5/5/25 (√25=5). The next one will be 6/6/36 (June 6, 2036).
Mental Math Trick
To quickly square a number ending with 5: Multiply the first digit(s) by itself plus one, then add 25. For 15²: 1×(1+1)=2, then add 25 → 225. For 25²: 2×3=6, then 625. This works for 35², 45², etc!





