Binary Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn the language of computers with simple explanations and interactive activities
What is the Binary Number System?

The binary number system is how computers understand and process information. Unlike our decimal system that uses 10 digits (0-9), binary uses only two digits: 0 and 1.
Why only two digits? Computers use electricity to work, and it's easier to represent information with just two states:
• 0 = OFF (no electricity)
• 1 = ON (electricity flowing)
Each binary digit is called a bit. A group of 8 bits is called a byte, which can represent a single character like 'A' or '7'.
Key Concept
Binary is a base-2 number system, while our everyday numbers use base-10. This means each position represents a power of 2 instead of a power of 10.
How the Binary System Works
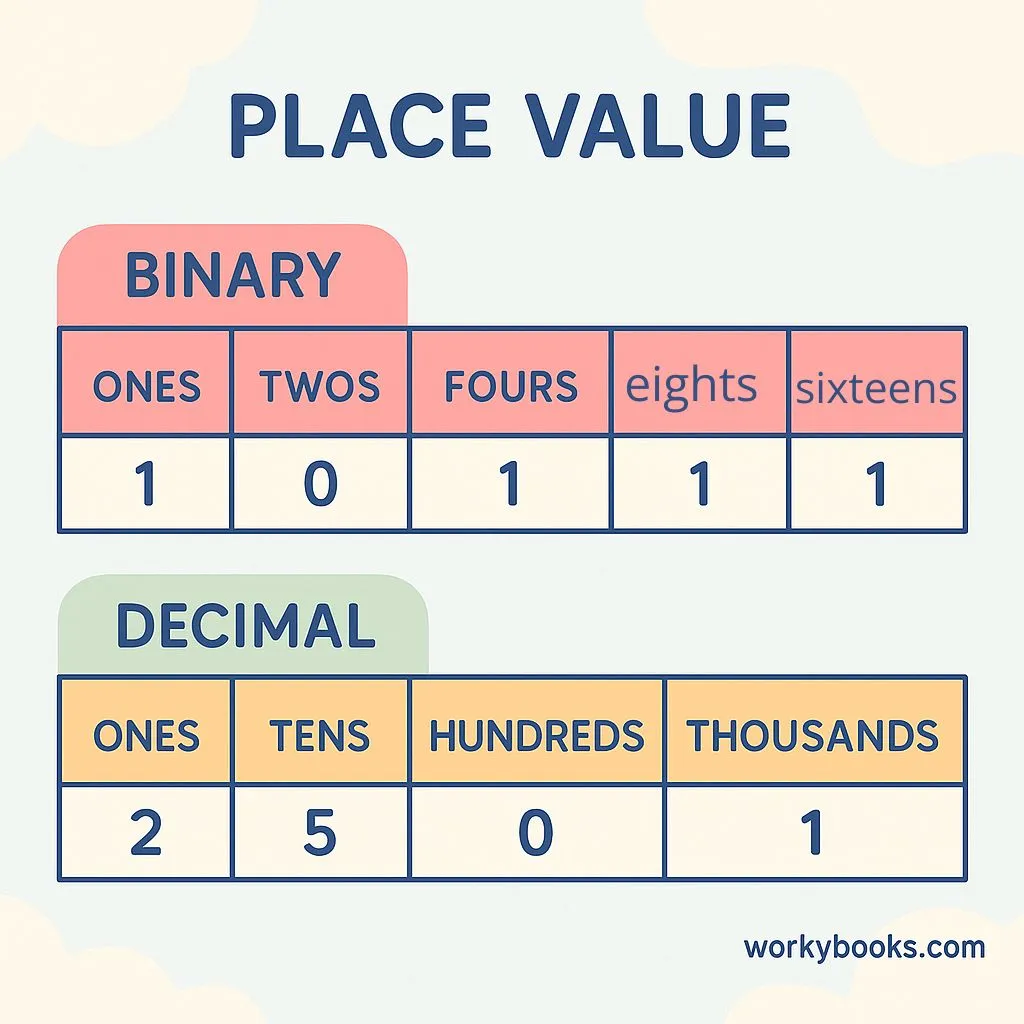
In binary, each digit's position represents a power of 2, starting from the right:
To find the decimal value of a binary number:
1. Write the binary digits
2. Multiply each digit by its place value
3. Add all the results together
Example: Binary 1011
= (1×8) + (0×4) + (1×2) + (1×1)
= 8 + 0 + 2 + 1
= 11 in decimal
Remember
The rightmost bit is called the Least Significant Bit (LSB), and the leftmost is the Most Significant Bit (MSB).
Binary Conversion Methods
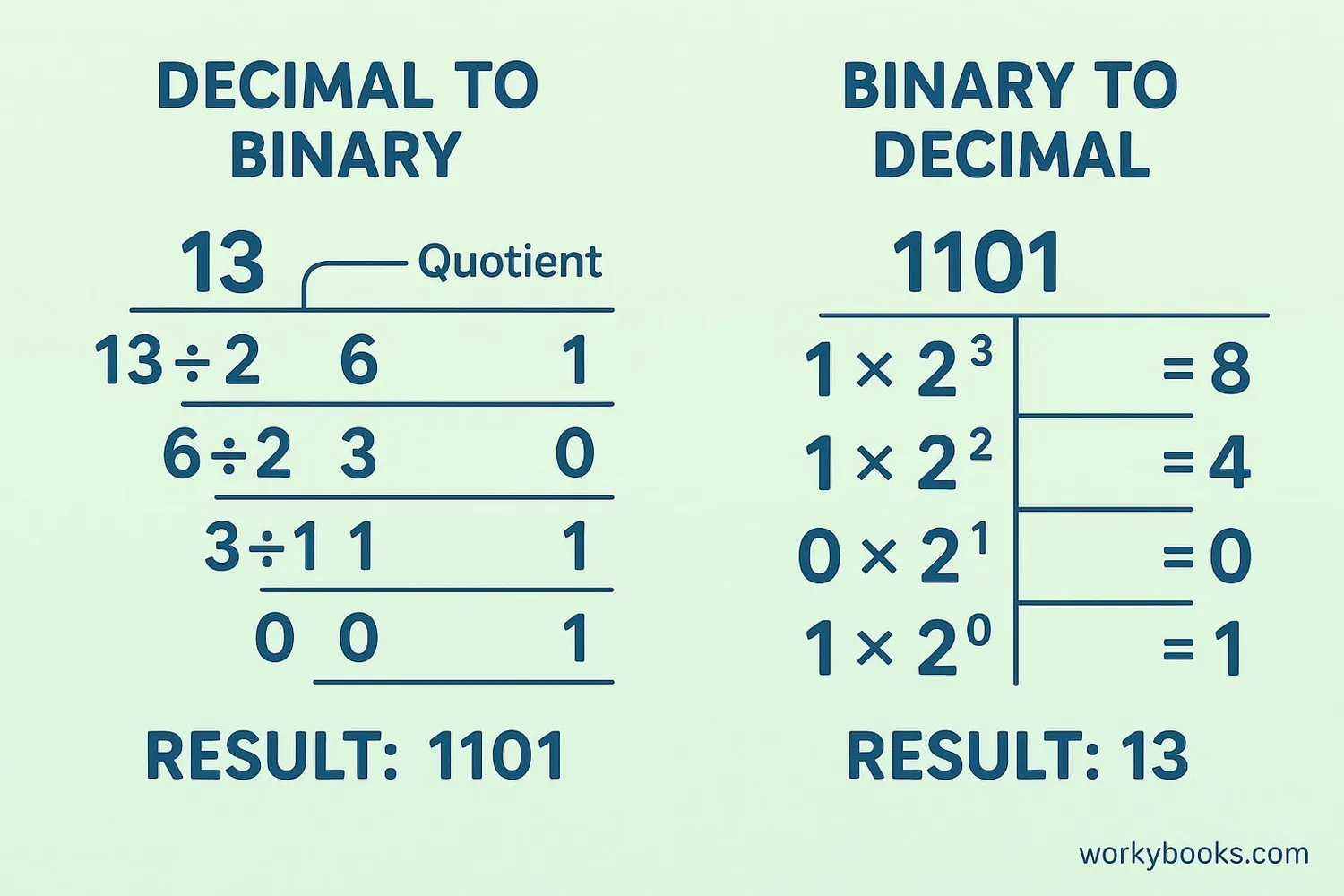
Decimal to Binary Conversion
To convert a decimal number to binary:
1. Divide the number by 2
2. Write down the remainder (0 or 1)
3. Divide the quotient by 2 again
4. Repeat until the quotient is 0
5. The binary number is the remainders read from bottom to top
Example: Convert 13 to binary
13 ÷ 2 = 6 remainder 1 ↑
6 ÷ 2 = 3 remainder 0 ↑
3 ÷ 2 = 1 remainder 1 ↑
1 ÷ 2 = 0 remainder 1 ↑
Binary: 1101
Binary to Decimal Conversion
To convert binary to decimal:
1. Write down the place values (1,2,4,8,16,... from right)
2. Multiply each binary digit by its place value
3. Add all the products together
Example: Convert 10101 to decimal
Place values: 16, 8, 4, 2, 1
Calculation: (1×16) + (0×8) + (1×4) + (0×2) + (1×1) = 16+0+4+0+1 = 21
Try It Yourself!
Real-World Examples

Binary is used everywhere in computing:
1. Text Representation: Each letter has a binary code. For example:
'B' = 01000010
'C' = 01000011
3. Sound: Music and sounds are converted to binary by measuring sound waves many times per second.
4. Computer Programs: All software and apps are written using binary instructions that tell the computer what to do.
5. Data Storage: Your files, photos, and videos are all stored as long sequences of 0s and 1s on your device.
Did You Know?
A single high-quality photo can contain millions of binary digits!
Binary Numbers Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about binary numbers:
Computer Number Trivia
Discover interesting facts about numbers in computing:
First Computer Program
Ada Lovelace wrote the first computer program in the 1840s for Charles Babbage's Analytical Engine. Her notes included what's now considered the first algorithm intended for machine processing.
Massive Numbers
A single terabyte (TB) of storage can hold about 8,000,000,000,000 bits! That's enough for approximately 300 hours of HD video or 250,000 photos.
Processing Speed
A modern computer processor can perform billions of binary calculations per second. A 3 GHz processor performs about 3,000,000,000 operations each second!
Space Computers
The Apollo Guidance Computer that took astronauts to the moon had only 64 kilobytes of memory and operated at 0.043 MHz - less powerful than a modern calculator!





