Circle Theorems - Definition, Examples, Quiz, FAQ, Trivia
Learn about circle rules with simple explanations, diagrams, and practice activities
What are Circle Theorems?
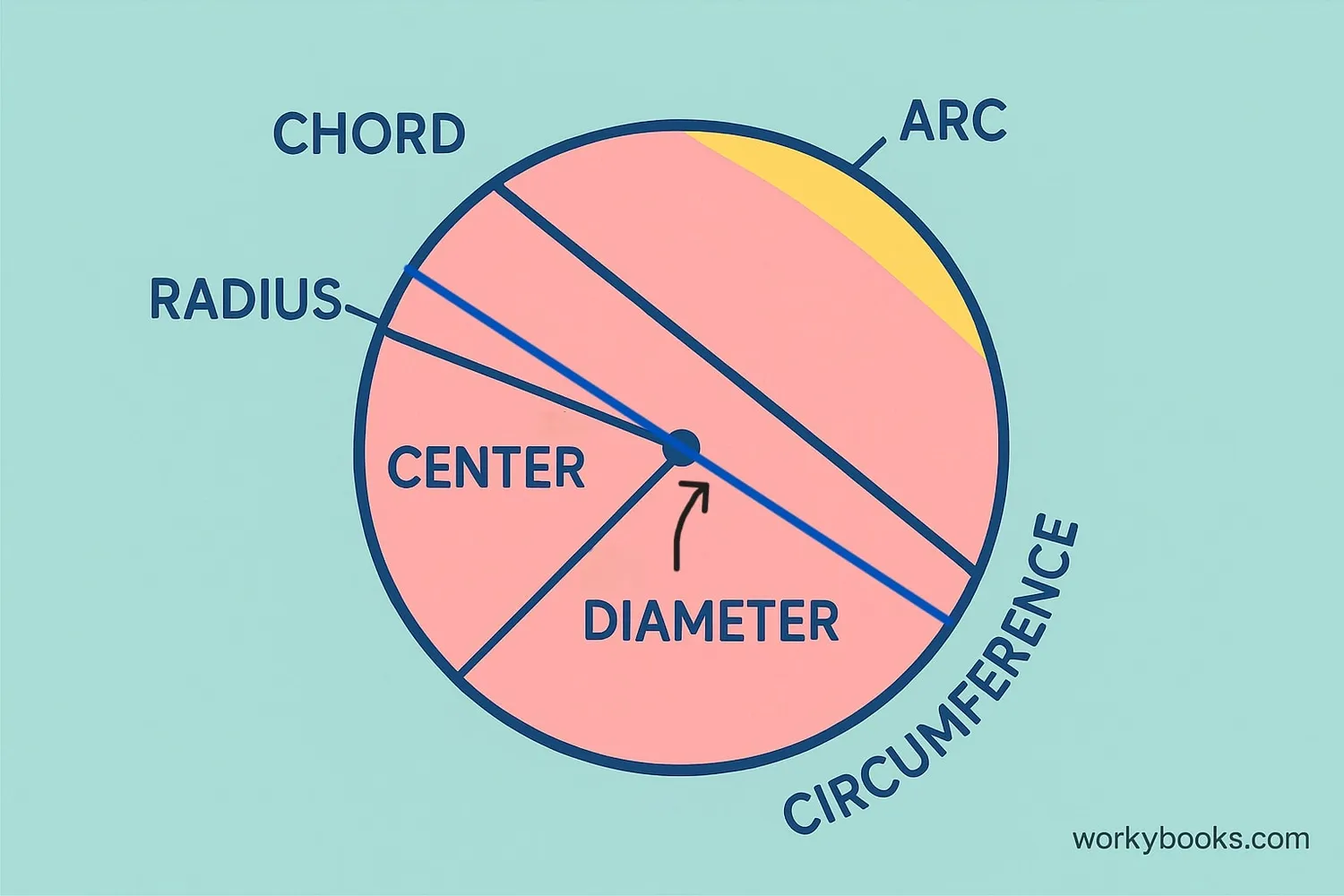
Circle theorems are special rules that describe how angles and lines work inside and around circles. They help us solve geometry problems involving circles without measuring everything.
Circles are everywhere - in wheels, coins, and even the sun! Understanding circle theorems helps us see the patterns and relationships in these shapes.
Circle theorems are like secret codes that unlock the mysteries of circles. Once you know them, you can solve many circle problems quickly and easily!
Key Concept
A circle is a set of points that are all the same distance from a center point. The distance from the center to any point on the circle is called the radius.
Circle Theorems List
Here are the most important circle theorems you should know:
Angle at the Center Theorem
The angle at the center of a circle is twice the angle at the circumference when both angles stand on the same arc.
Angle in a Semicircle Theorem
An angle inscribed in a semicircle is always a right angle (90 degrees).
Angles in Same Segment Theorem
Angles in the same segment of a circle are equal.
Cyclic Quadrilateral Theorem
In a cyclic quadrilateral (a 4-sided shape with all corners on a circle), opposite angles add up to 180 degrees.
Tangent Theorem
A tangent to a circle is perpendicular to the radius at the point of contact.
Alternate Segment Theorem
The angle between a tangent and a chord is equal to the angle in the alternate segment.
Remember
Circle theorems work for any circle, no matter how big or small it is. That's the magic of circles!
How to Use Circle Theorems
Using circle theorems is like solving a puzzle. Here's how to approach circle theorem problems:
Step-by-Step Guide
- Identify circle parts: Look for the center, radius, chords, tangents, and angles.
- Look for patterns: Notice if angles are at the center or circumference, or if there's a cyclic quadrilateral.
- Recall relevant theorems: Which theorem might apply to what you see?
- Apply the theorem: Use the theorem to create equations or find relationships.
- Solve step by step: Work through the problem logically, writing down each step.
- Check your answer: Does it make sense? Could you use another theorem to confirm?
Pro Tip
Always mark equal angles with the same number of arcs. This visual trick helps you see relationships more easily.
Circle Theorem Examples
Let's see how circle theorems work in practice:
Example 1: Angle at the Center
In a circle, an angle at the center is 120°. What is the angle at the circumference standing on the same arc?
Solution: Using the theorem: Angle at circumference = ½ × Angle at center = ½ × 120° = 60°
Example 2: Angle in a Semicircle
Triangle ABC is inscribed in a circle with AB as diameter. Angle at B is 40°. What is angle at C?
Solution: Since AB is diameter, angle at C is in a semicircle = 90°. So angle at C is 90°.
Example 3: Cyclic Quadrilateral
In cyclic quadrilateral ABCD, angle A = 85°, angle B = 95°. What are angles C and D?
Solution: Opposite angles add to 180°. So angle A + angle C = 180° → 85° + C = 180° → C = 95°
Angle B + angle D = 180° → 95° + D = 180° → D = 85°
Practice Tip
Try drawing your own circle diagrams and mark the angles. The more you practice, the easier it becomes to spot which theorem to use!
Circle Theorem Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about circle theorems:
Circle Trivia
Discover interesting facts about circles and their theorems:
Ancient Circles
The ancient Greeks studied circles over 2,500 years ago. Mathematicians like Euclid and Archimedes discovered many circle properties that we still use today.
Circles in Nature
Circles appear everywhere in nature - from the cross-section of tree trunks to the shape of planets and stars. Even bubbles form spheres, which are 3D circles!
Perfect Circles?
In mathematics, a circle is perfectly round, but in nature, perfect circles are rare. Even the most precise human-made circles have tiny imperfections when viewed closely.
Pi Day
March 14 (3/14) is celebrated as Pi Day because π (pi) is approximately 3.14. Pi is the ratio of a circle's circumference to its diameter, and it appears in many circle formulas.


