Constant Rate of Change - Definition, Examples, Quiz, FAQ, Trivia
Understanding slope, linear functions, and proportional relationships
What is Constant Rate of Change?
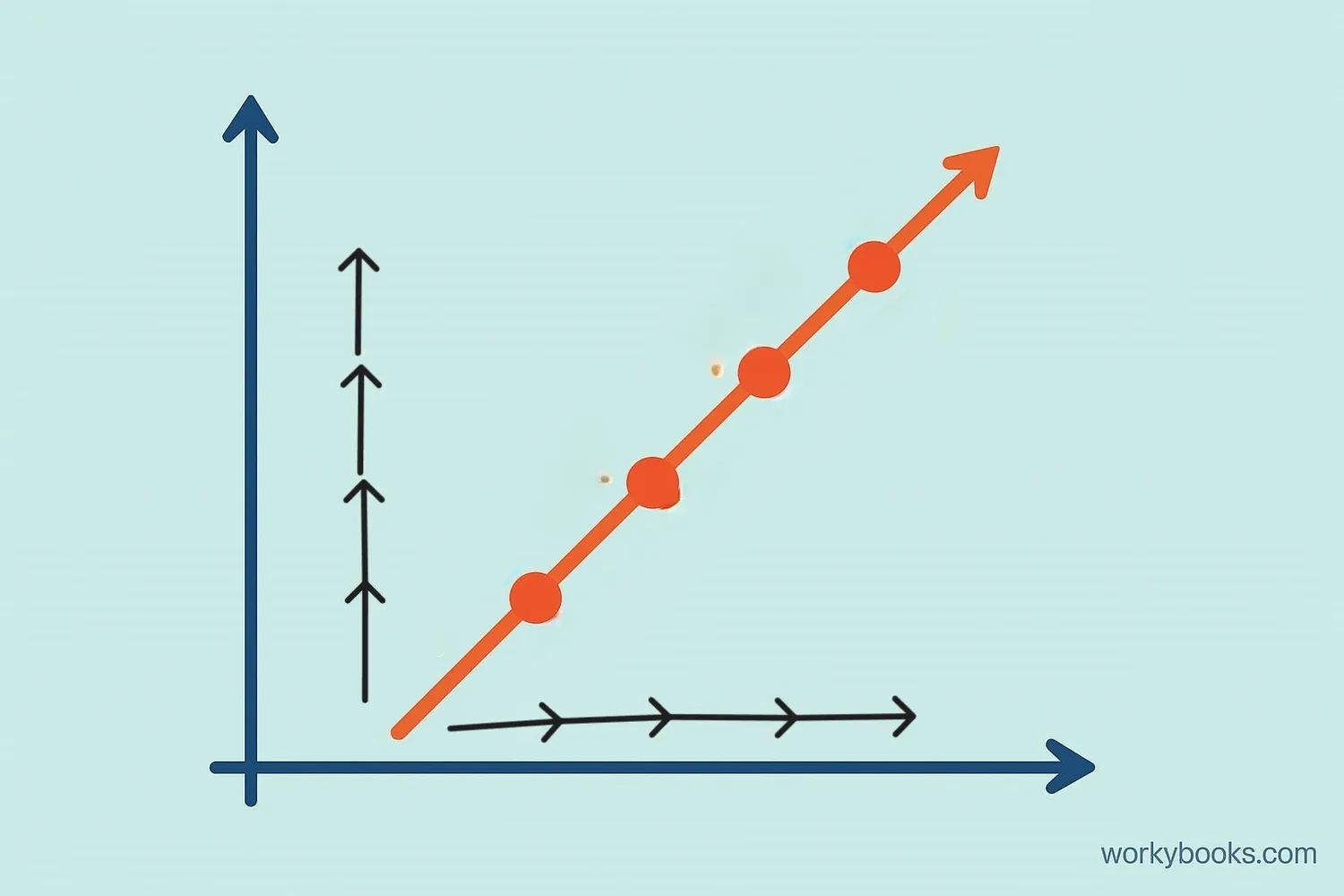
A constant rate of change means that something changes by the same amount over equal time periods or intervals. It's like walking at a steady pace: every minute you cover the same distance.
Imagine you're saving money. If you save $5 every week, that's a constant rate of change. The amount you save changes at a steady, predictable rate. In mathematics, this is often called a linear relationship because it creates a straight line when graphed.
Key characteristics of constant rate of change:
- The relationship between two quantities is proportional
- The graph is always a straight line
- The ratio between the two quantities stays the same
- It can be described by the equation y = mx + b
Key Concept
A constant rate of change means that for every unit increase in one quantity, the other quantity changes by a fixed amount.
How to Find Constant Rate of Change
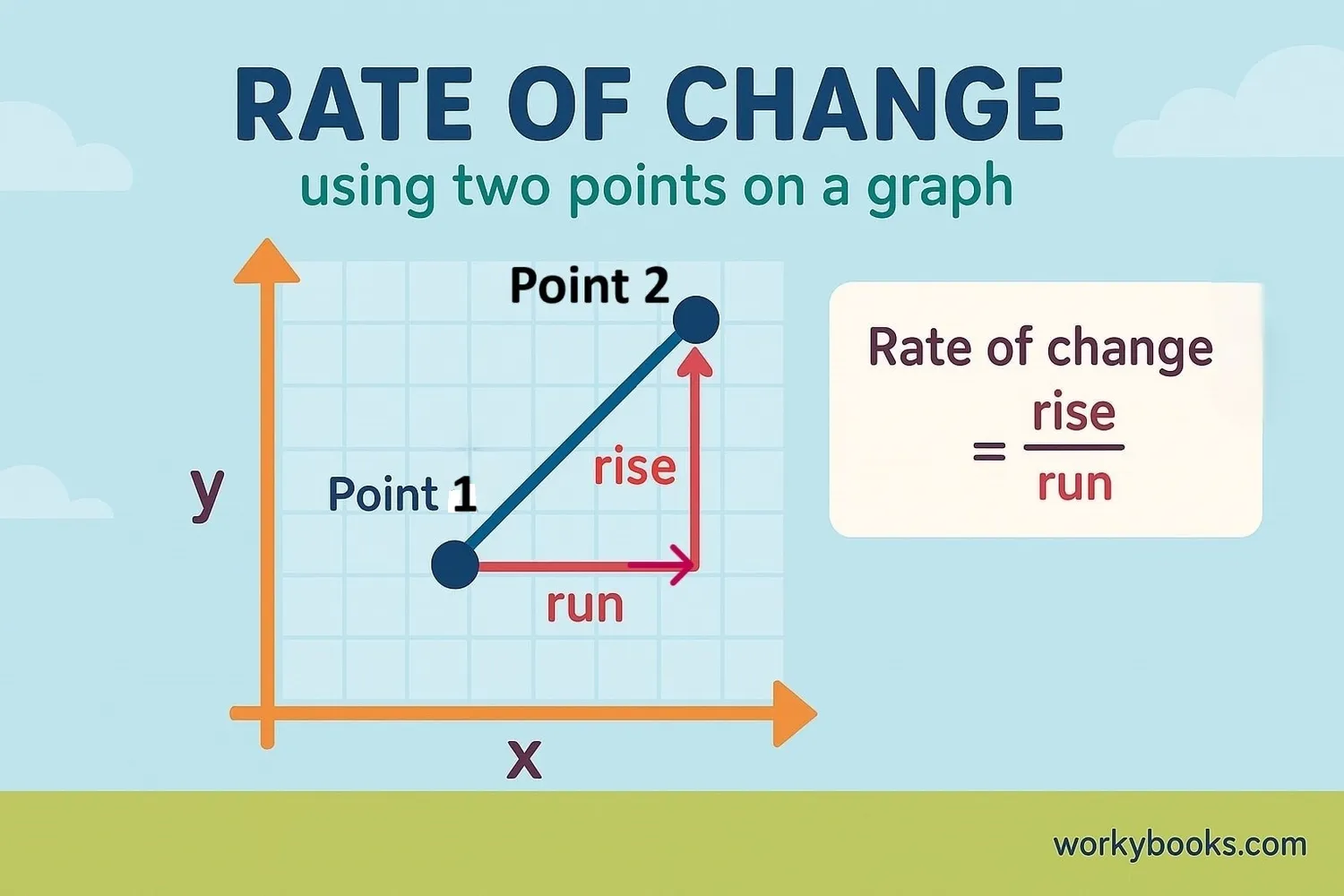
You can find the constant rate of change using this simple formula:
Rate of Change Formula
This is also known as "rise over run" when looking at a graph.
Time & Distance Example
| Time (hours) | Distance (miles) |
|---|---|
| 0 | 0 |
| 1 | 50 |
| 2 | 100 |
| 3 | 150 |
To find the rate of change, pick any two points. Between hour 1 and hour 2:
Change in time (x) = 2 - 1 = 1 hour
Change in distance (y) = 100 - 50 = 50 miles
Rate of change = 50 miles / 1 hour = 50 miles per hour
Remember
Constant rate of change means the ratio between two quantities is always the same. If one quantity doubles, the other doubles too.
Slope and Linear Functions
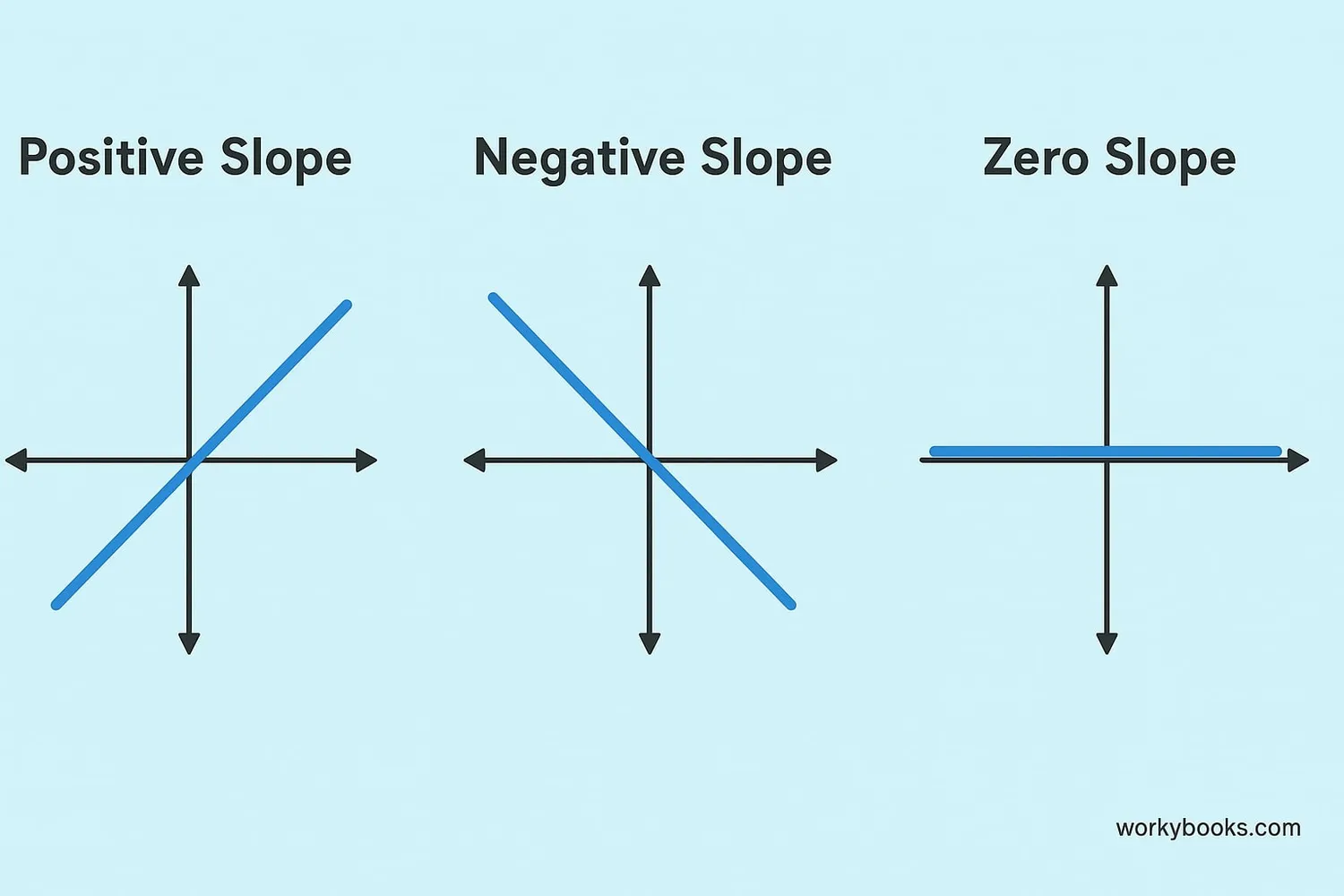
In mathematics, the constant rate of change is called slope. It's a measure of how steep a line is. Slope is represented by the letter m in the equation of a line:
Slope-Intercept Form
Where m is the slope (rate of change) and b is the y-intercept (starting point).
- Positive slope: The line goes upward from left to right (increasing)
- Negative slope: The line goes downward from left to right (decreasing)
- Zero slope: The line is horizontal (no change)
- Undefined slope: The line is vertical (not a function)
Connection
Slope is just another name for constant rate of change. They mean the same thing!
Real-World Examples
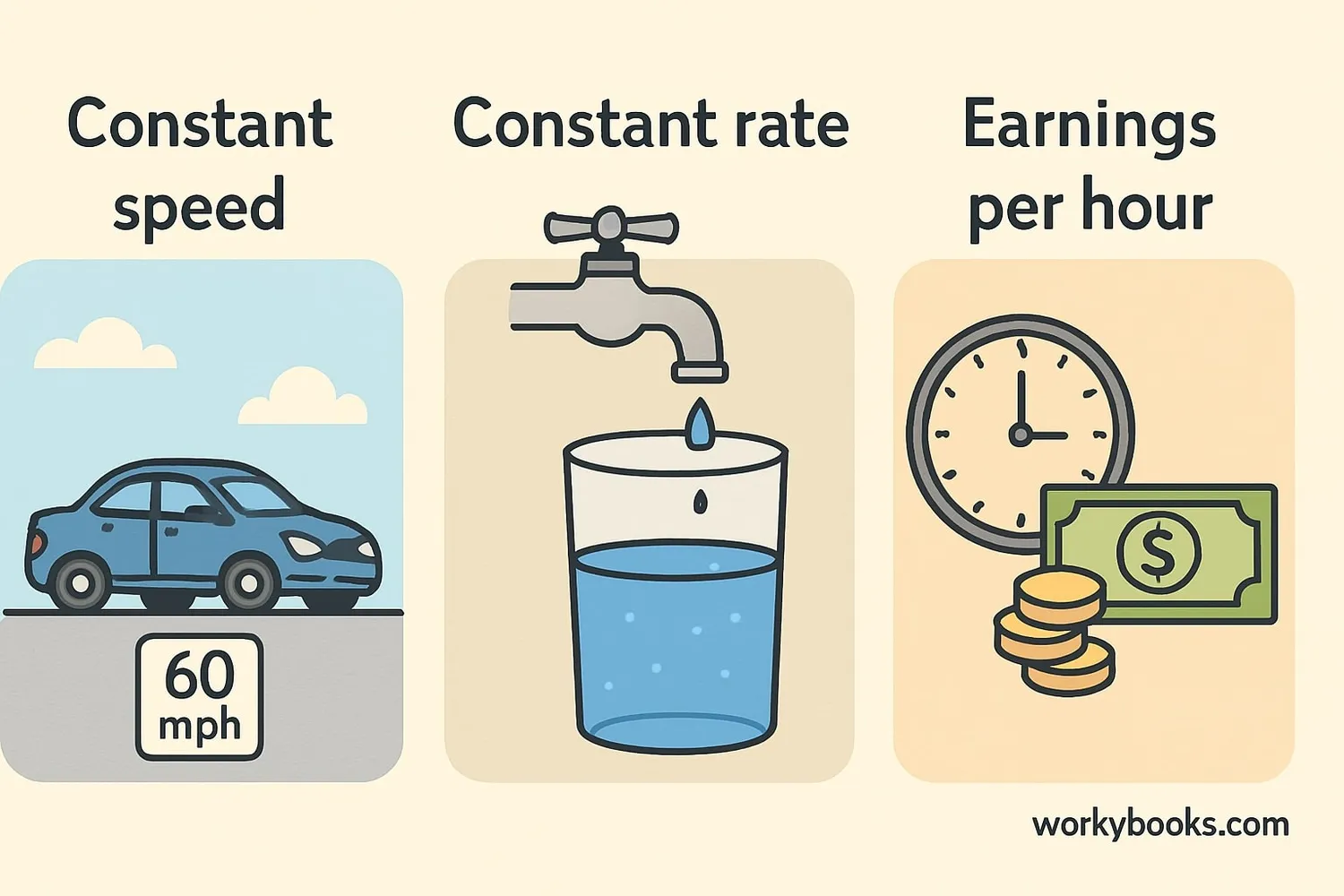
Constant rate of change is all around us! Here are some common examples:
1. Driving at Constant Speed
If a car travels at 60 miles per hour, its distance changes at a constant rate. In 1 hour it travels 60 miles, in 2 hours 120 miles, and so on.
2. Filling a Swimming PoolIf water flows into a pool at 100 gallons per minute, the amount of water increases at a constant rate. After 1 minute: 100 gallons, after 2 minutes: 200 gallons, etc.
3. Earning MoneyIf you earn $15 per hour, your total earnings increase at a constant rate. Work 1 hour: $15, work 2 hours: $30, work 3 hours: $45.
4. Plant GrowthSome plants grow at a constant rate. If a plant grows 2 inches per week, after 1 week it's 2 inches tall, after 2 weeks 4 inches, after 3 weeks 6 inches.
Try It Yourself
Look for constant rates of change in your daily life - how fast your family uses milk, how many pages you read per day, or how your height changes over time!
Practice Quiz
Test your understanding of constant rate of change with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about constant rate of change:
Math Trivia
Discover interesting facts about rates and measurement:
Ancient Measurement
The concept of constant rate of change dates back to ancient Egypt, where builders used constant slopes to construct pyramids with precise angles.
Galileo's Discovery
Galileo discovered that falling objects accelerate at a constant rate due to gravity. This constant acceleration is approximately 9.8 m/s².
Space Travel
Rocket scientists use constant rates of change to calculate fuel consumption during space missions. A small miscalculation can lead to missing the target!
Speed Records
The fastest constant speed ever achieved by a vehicle is 763 mph (1,228 km/h) by the Thrust SSC jet car in 1997. That's faster than the speed of sound!





