Degree of a Polynomial - Definition, Examples, Quiz, FAQ, Trivia
Learn about polynomials, their degrees, and types with easy explanations and practice activities
What is a Polynomial?
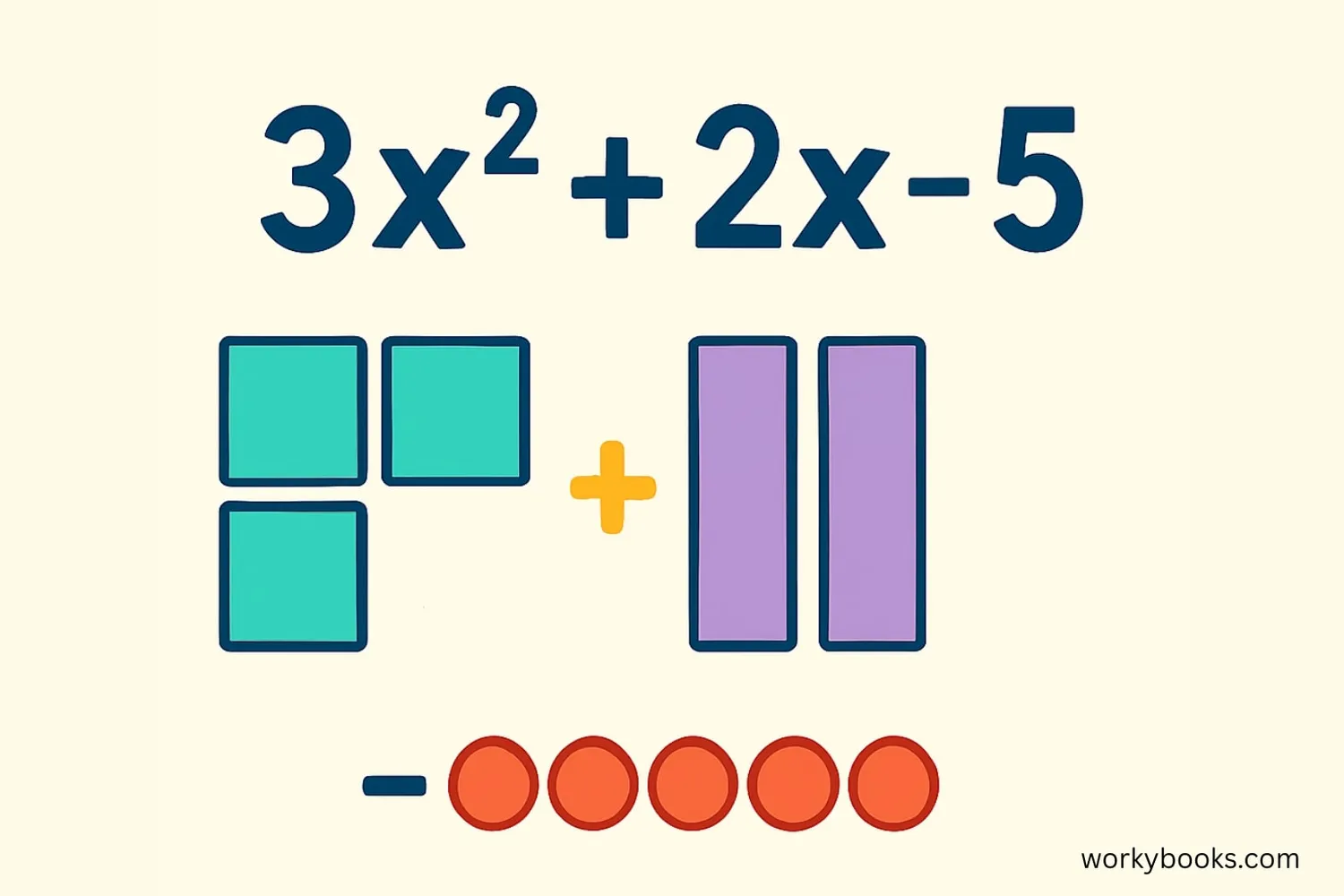
A polynomial is a mathematical expression made up of terms. Each term can include:
- Numbers (called coefficients like 3, 2, 5)
- Variables (like x or y)
- Exponents (like the 2 in x²)
Polynomials are connected using addition (+) or subtraction (-) operations.
Here's an example of a polynomial:
Key Concept
Polynomials can have constants (like 5), variables (like x), and exponents (like ²), but they never have division by a variable or negative exponents.
Polynomial Terms

Polynomials are made of terms separated by + or - signs. Each term has three important parts:
1. Coefficient: The number in front of the variable
2. Variable: The letter that represents an unknown value
3. Exponent: The small number that shows how many times the variable is multiplied
Let's look at this polynomial:
4x³ (coefficient: 4, variable: x, exponent: 3)
-2x² (coefficient: -2, variable: x, exponent: 2)
7x (coefficient: 7, variable: x, exponent: 1)
-9 (constant term, no variable)
The leading term is the term with the highest exponent. In this case, it's 4x³.
Remember
The constant term (like -9) has no variable. We can think of it as having an exponent of 0, since any number to the power of 0 is 1.
Degree of a Polynomial
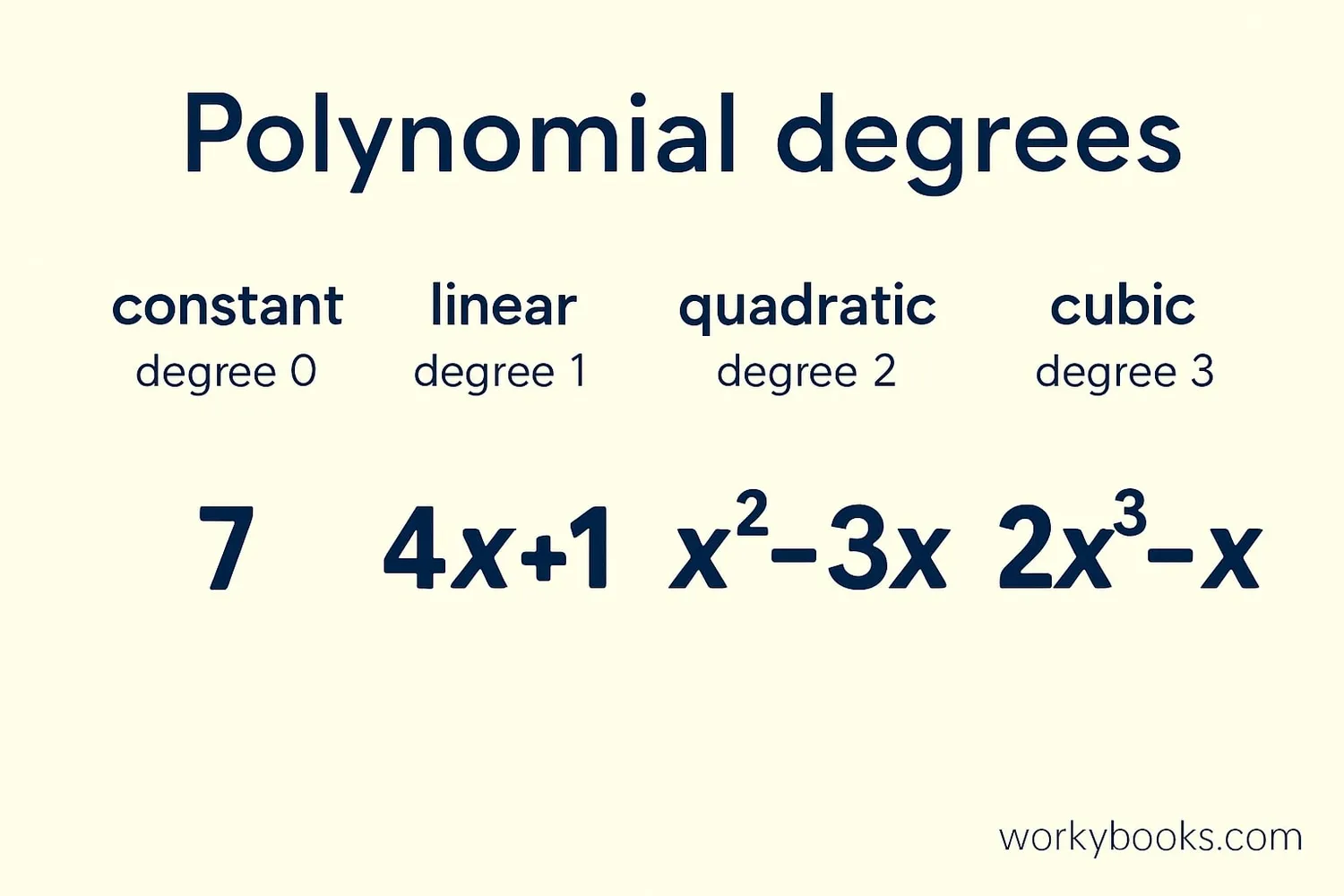
The degree of a polynomial is the highest exponent of its variable. It tells us about the polynomial's "power" and helps us understand its behavior.
How to find the degree:
1. Look at each term's exponent
2. Find the largest exponent
3. That's the degree of the polynomial!
Example:
The degree helps us name polynomials:
- Degree 0: Constant polynomial
- Degree 1: Linear polynomial
- Degree 2: Quadratic polynomial
- Degree 3: Cubic polynomial
- Degree 4: Quartic polynomial
Important
The degree of a constant polynomial (like 5 or -2) is 0 because we can write it as 5x⁰.
Types of Polynomials

Polynomials can be classified in two ways: by the number of terms they have, and by their degree.
By Number of Terms:
- Monomial: A polynomial with only one term (e.g., 3x²)
- Binomial: A polynomial with two terms (e.g., 2x + 5)
- Trinomial: A polynomial with three terms (e.g., x² + 3x - 4)
By Degree:
- Constant: Degree 0 (e.g., 7 or -3)
- Linear: Degree 1 (e.g., 2x + 3)
- Quadratic: Degree 2 (e.g., x² - 4x + 4)
- Cubic: Degree 3 (e.g., 4x³ - 3x² + 2x - 1)
- Quartic: Degree 4 (e.g., x⁴ - 16)
Knowing these types helps us understand how to work with different polynomials.
Tip
When classifying a polynomial, you can mention both its type by terms and by degree. For example: "This quadratic trinomial" for x² - 4x + 4.
Examples

Let's practice identifying polynomials and finding their degrees:
Example 1: 2x - 5
- Number of terms: 2 (binomial)
- Highest exponent: 1
- Degree: 1 (linear)
Example 2: x³ + 4x² - 7x + 2
- Number of terms: 4 (no special name)
- Highest exponent: 3
- Degree: 3 (cubic)
Example 3: 5x⁴
- Number of terms: 1 (monomial)
- Highest exponent: 4
- Degree: 4 (quartic)
Example 4: 10
- Number of terms: 1 (monomial)
- Highest exponent: 0
- Degree: 0 (constant)
Now try these yourself:
1. 3x² - 2x + 1
2. 7x - 4
3. 9
Practice Tip
Always write polynomials in standard form (terms from highest to lowest exponent) to easily identify the leading term and degree.
Polynomial Practice Quiz
Test your understanding of polynomials with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about polynomials:
Math Trivia
Discover interesting facts about polynomials and mathematics:
Ancient Polynomials
The earliest known work with polynomial equations dates back to Babylonian mathematicians around 2000 BC! They solved quadratic equations on clay tablets without using modern algebraic notation.
Polynomials in Space
NASA uses polynomials to calculate spacecraft trajectories. The paths of planets and spacecraft can be modeled using polynomial equations that account for gravity and motion.
The Polynomial Record
The longest polynomial ever written had over 1,200 terms! Mathematicians sometimes work with very high-degree polynomials to model complex systems like weather patterns.
Word Origins
The word "polynomial" comes from Greek: "poly" meaning "many" and "nomial" meaning "term". So polynomial literally means "many terms" - a perfect description!





