Diagonal of a Cube - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate face diagonals and space diagonals of cubes with step-by-step examples
What is a Cube?
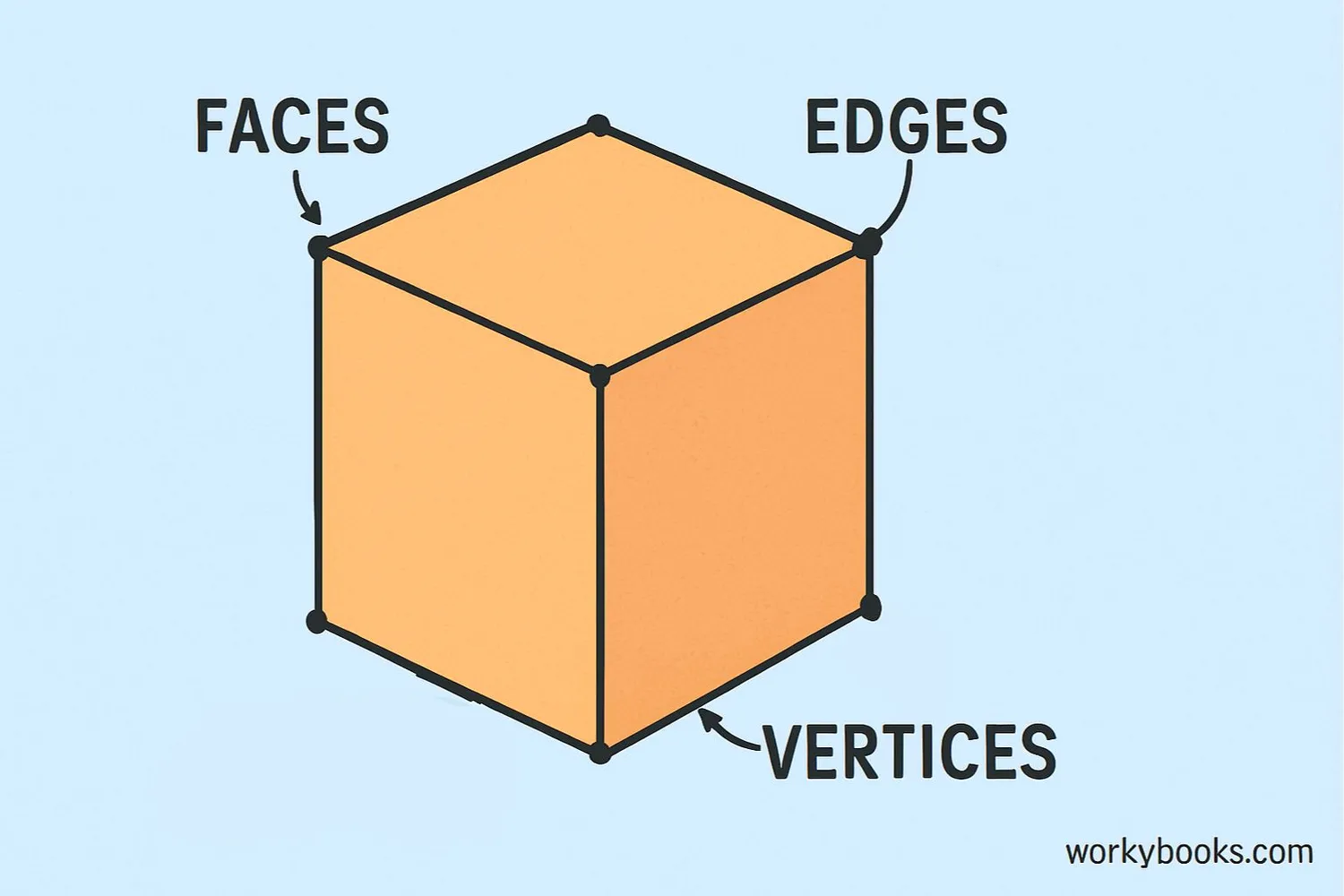
A cube is a special three-dimensional shape where all sides are equal squares. It's like a box with six identical faces.
Key properties of a cube:
- All faces are perfect squares
- All edges are equal in length
- All angles are right angles (90 degrees)
- It has 6 faces, 12 edges, and 8 vertices (corners)
Faces
All identical squares
Edges
All equal in length
Vertices
Corners where edges meet
Key Concept
The most important thing about a cube is that all edges are the same length. We call this length "s" (for side length).
Diagonals in a Cube
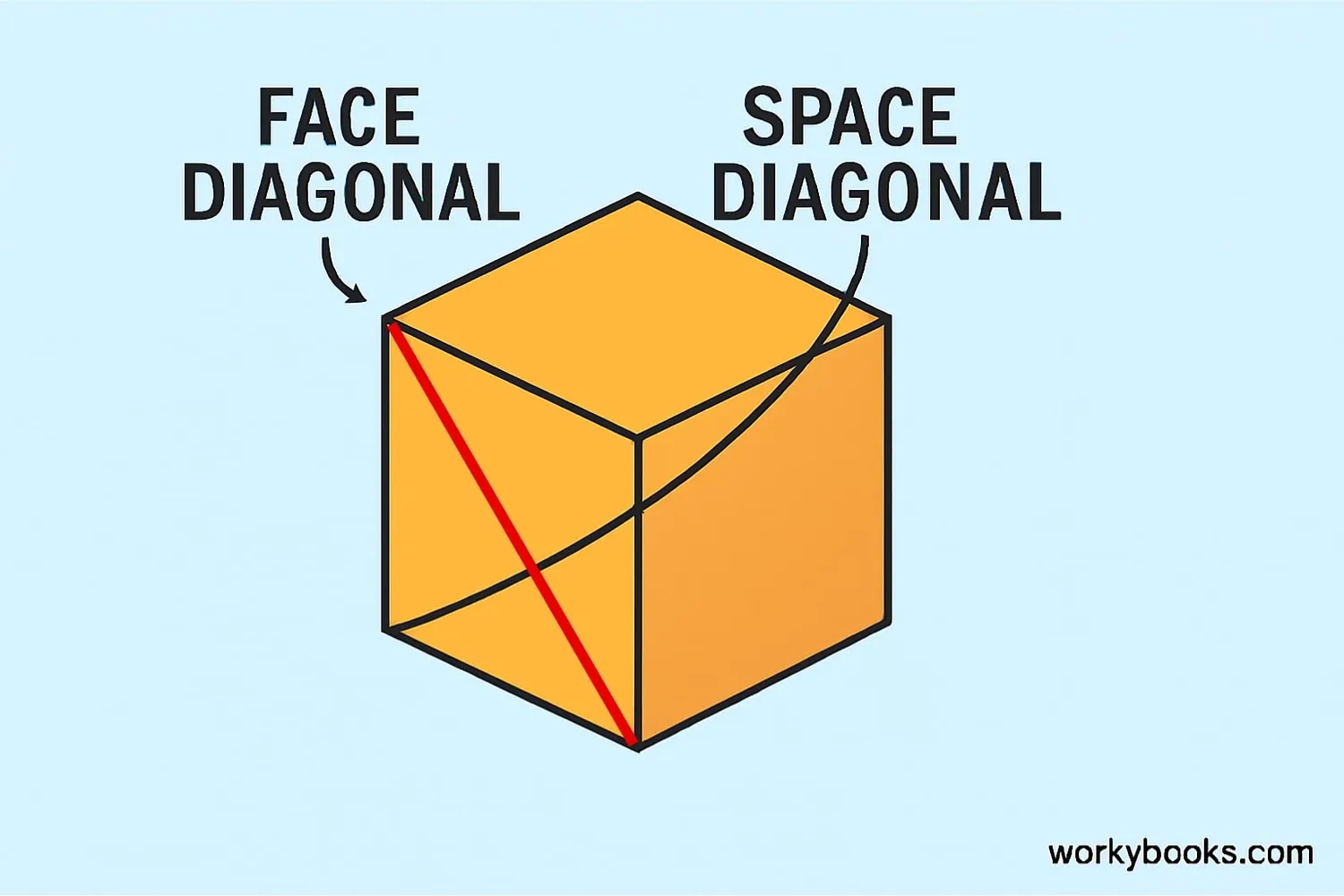
There are two types of diagonals in a cube:
1. Face Diagonal: This is a line connecting two opposite corners on the same face of the cube.
It stays on the surface and doesn't go through the inside of the cube.
2. Space Diagonal: This is a line connecting two opposite corners of the cube, going through its interior.
It passes through the inside of the cube from one corner to the farthest corner.
Remember
Face diagonals stay on the cube's surface, while space diagonals go through the inside of the cube.
Diagonal Formulas
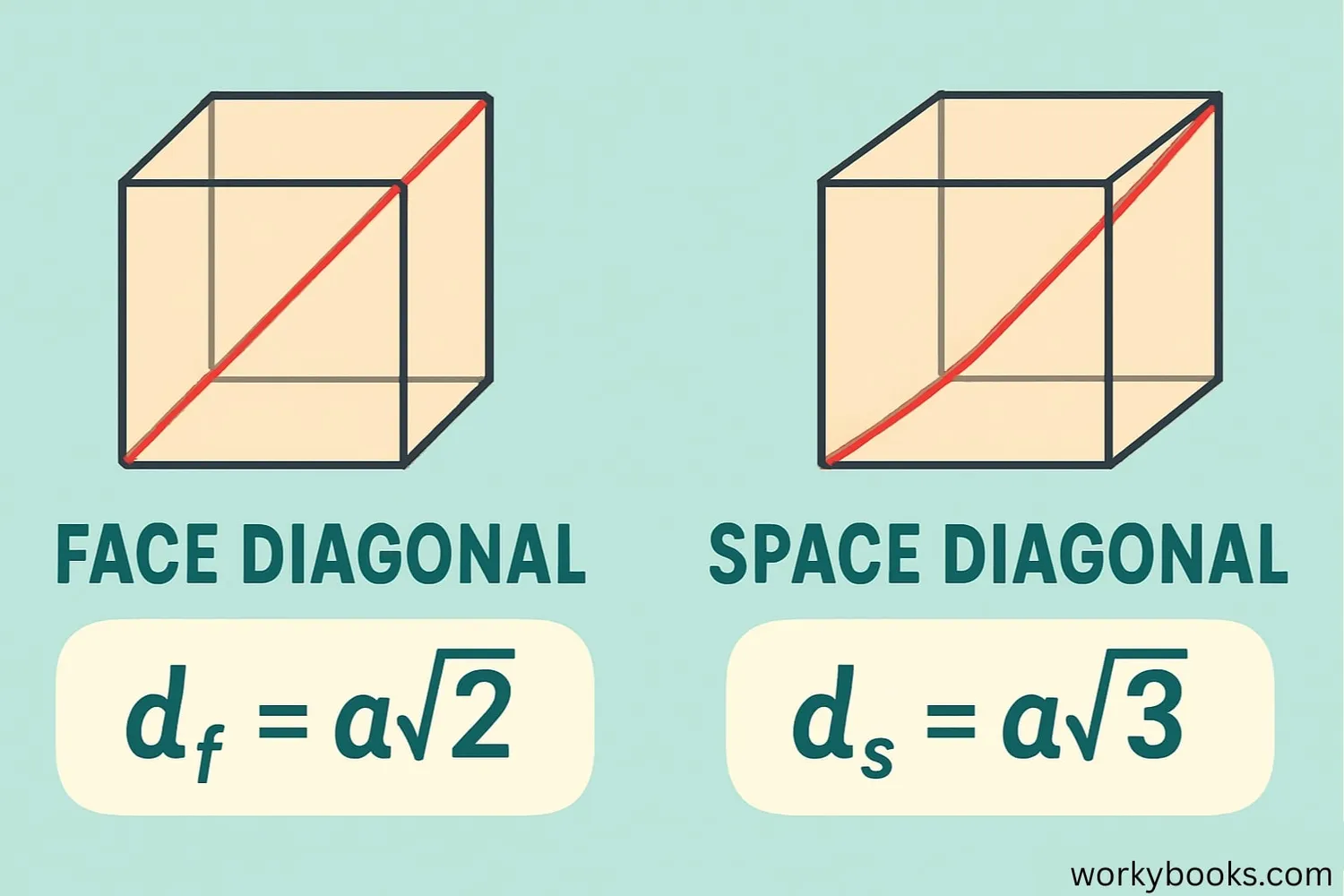
The formulas for calculating diagonals depend on the length of the cube's edge (s).
Face Diagonal Formula
The face diagonal is √2 times the side length
Space Diagonal Formula
The space diagonal is √3 times the side length
Math Tip
√2 is approximately 1.414 and √3 is approximately 1.732. You can use these values to estimate diagonals.
How to Calculate Diagonals
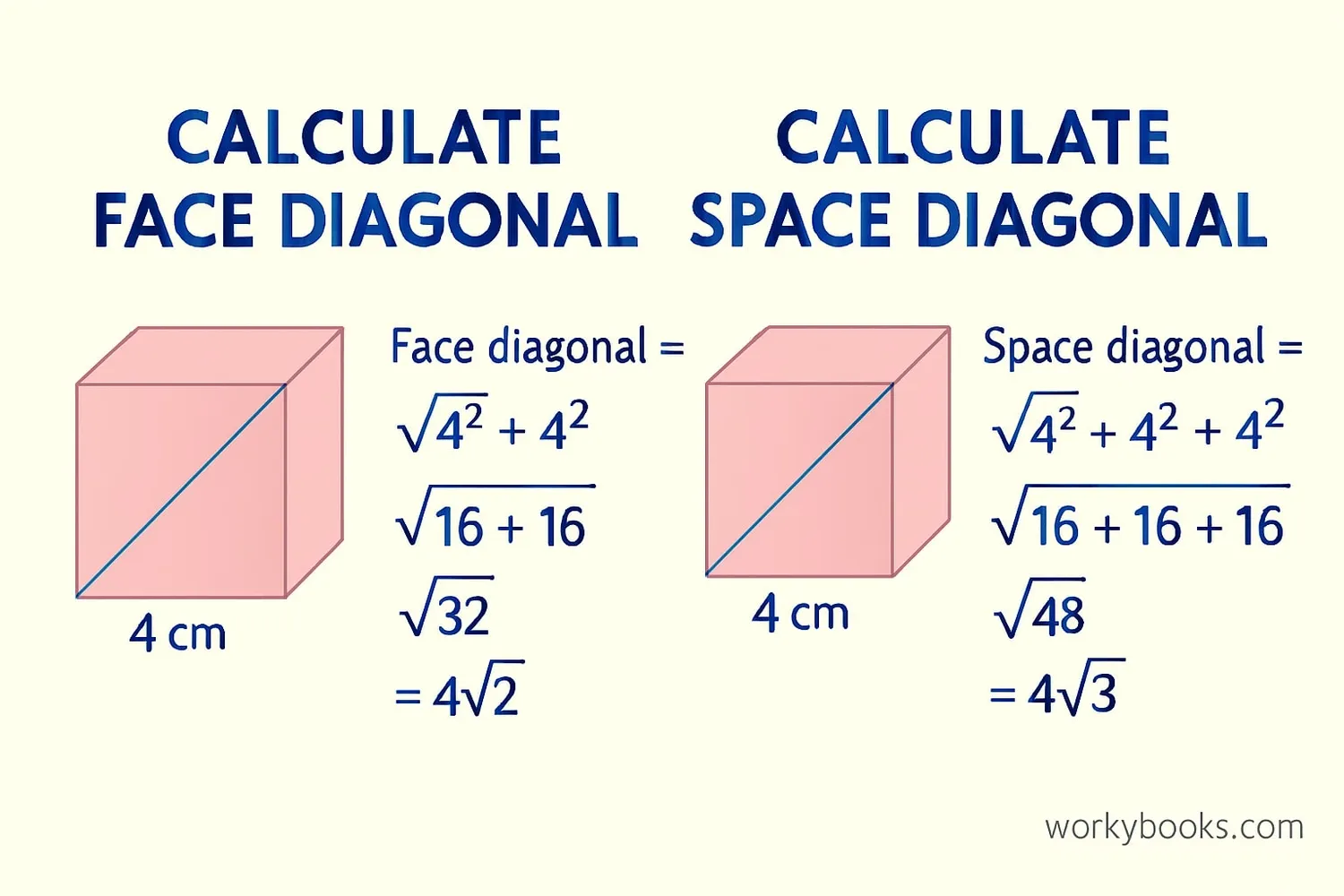
Let's practice calculating diagonals for a cube with side length s = 4 cm:
Step 1: Identify the side length
s = 4 cm
Step 2: Calculate the face diagonal
dface = s × √2 = 4 × 1.414 ≈ 5.656 cm
Step 3: Calculate the space diagonal
dspace = s × √3 = 4 × 1.732 ≈ 6.928 cm
Step 4: Interpret the results
The longest line you can draw on a face is about 5.66 cm. The longest line through the whole cube is about 6.93 cm.
Calculation Tip
Space diagonal is always longer than face diagonal because it crosses more space inside the cube.
Real-World Examples
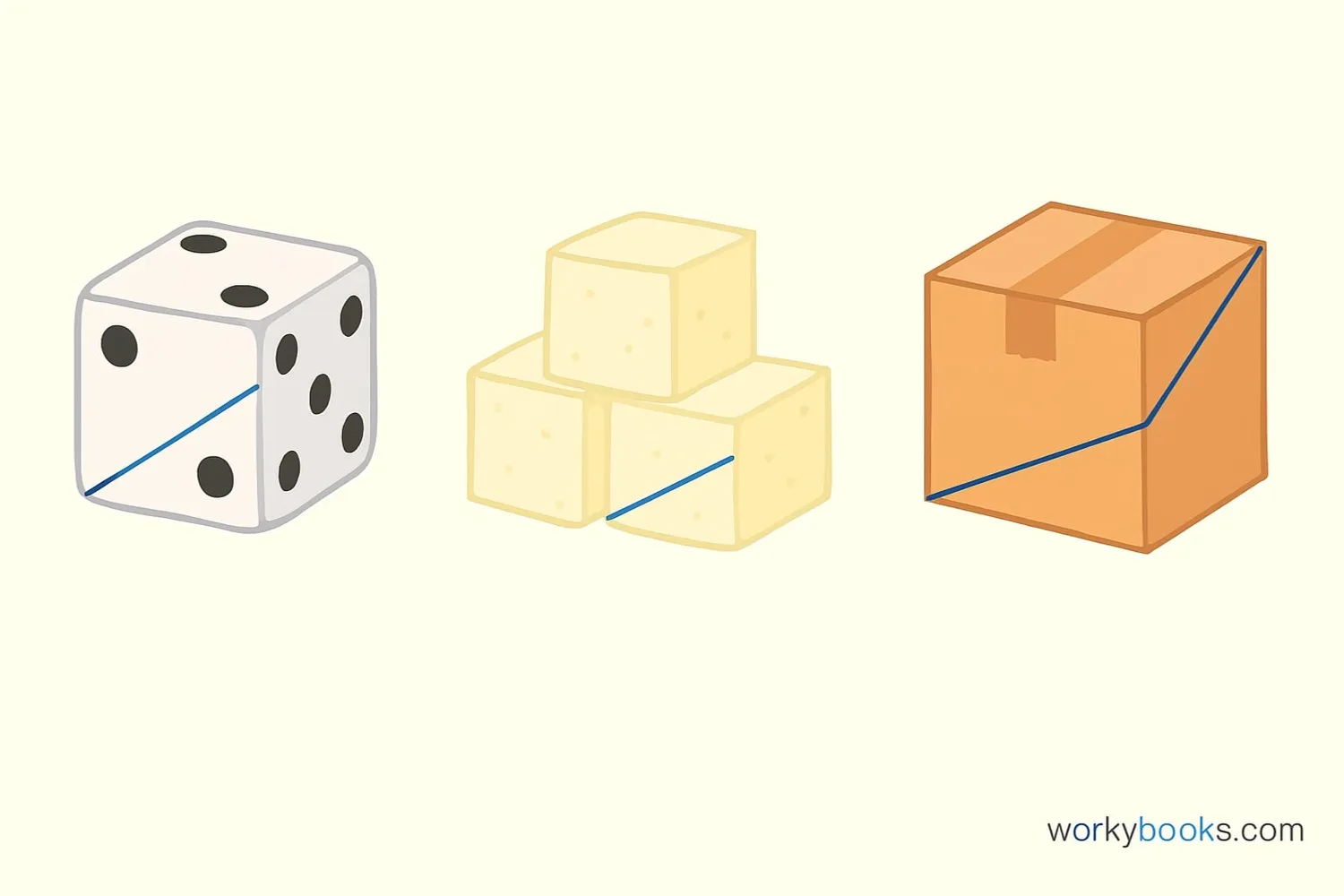
Let's see how diagonal calculations work with real objects:
Example 1: A Rubik's Cube
Side length: 5.7 cm
Face diagonal = 5.7 × √2 ≈ 5.7 × 1.414 ≈ 8.06 cm
Space diagonal = 5.7 × √3 ≈ 5.7 × 1.732 ≈ 9.87 cm
Example 2: A Sugar Cube
Side length: 1.5 cm
Face diagonal = 1.5 × √2 ≈ 1.5 × 1.414 ≈ 2.12 cm
Space diagonal = 1.5 × √3 ≈ 1.5 × 1.732 ≈ 2.60 cm
Example 3: A Large Storage Box
Side length: 40 cm
Face diagonal = 40 × √2 ≈ 40 × 1.414 ≈ 56.56 cm
Space diagonal = 40 × √3 ≈ 40 × 1.732 ≈ 69.28 cm
Real-World Tip
Knowing diagonal lengths helps when packing boxes or determining if objects will fit through spaces.
Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about cube diagonals:
Geometry Trivia
Discover interesting facts about cubes and diagonals:
Ancient Cubes
The oldest known dice (cubes) date back over 5,000 years to ancient Mesopotamia. These early cubes were made from materials like bone, wood, and pottery.
Crystal Cubes
In nature, pyrite (fool's gold) often forms perfect cube-shaped crystals. These natural cubes form because of the arrangement of atoms in their molecular structure.
Molecular Cubes
Salt crystals form cube shapes because sodium and chloride ions arrange themselves in a cubic lattice structure at the molecular level.
Cube Roots
The space diagonal formula helps explain why cube roots are called "cube" roots - because if you have a cube with volume V, the side length is ∛V (the cube root of V).





