Diagonal of a Rectangle - Definition, Examples, Quiz, FAQ, Trivia
Learn about rectangle diagonals with simple explanations, formulas, and practice activities
What is the Diagonal of a Rectangle?
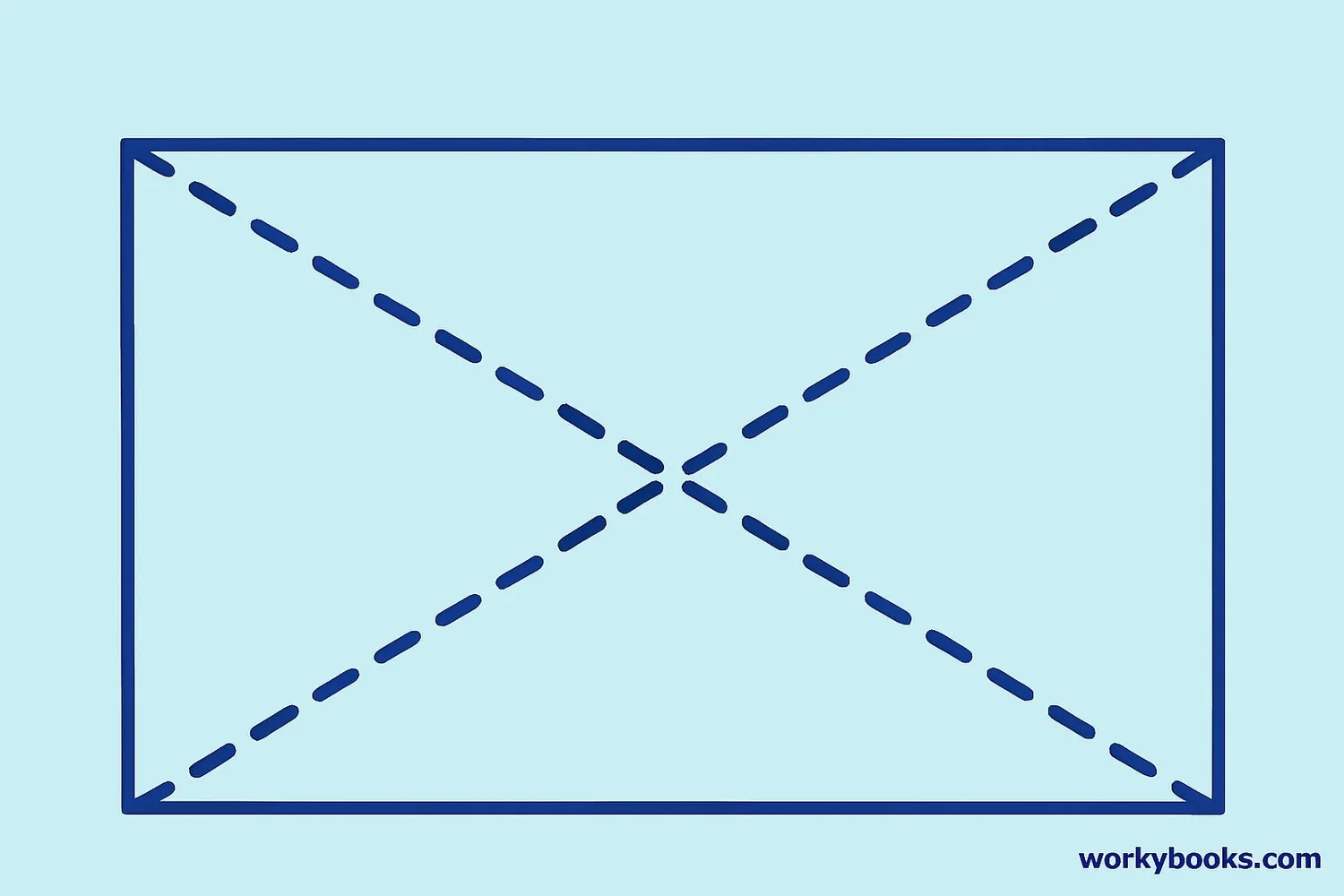
A diagonal is a straight line connecting two opposite corners of a rectangle. Every rectangle has two diagonals that are equal in length. These diagonals cross each other at the center of the rectangle.
Diagonals are important in geometry because they help us understand the properties of shapes and solve problems involving rectangles. They also connect the rectangle's opposite vertices (corners).
Imagine a rectangle like a door. The diagonal would be the line from the top-left corner to the bottom-right corner, or from the top-right to the bottom-left corner. Both diagonals are always the same length in a rectangle!
Key Concept
Every rectangle has two diagonals that are always equal in length and bisect each other at the center.
Properties of Rectangle Diagonals
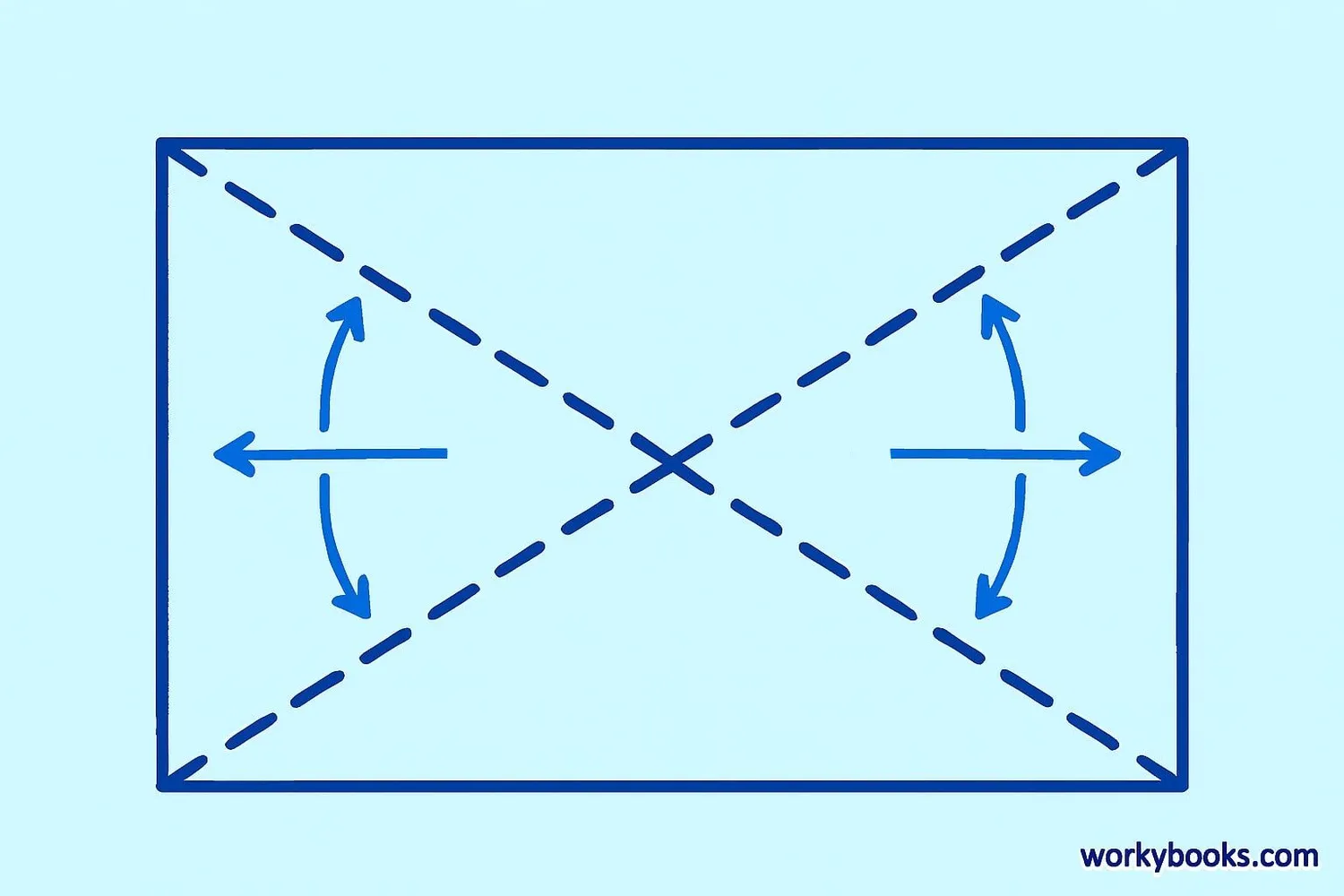
Rectangles have special properties that make their diagonals interesting:
1. Equal Length: Both diagonals in a rectangle are always equal. If you measure one diagonal, the other will be exactly the same length.
2. Bisect Each Other: The diagonals cross exactly at their midpoint. This means each diagonal is divided into two equal parts at the center.
3. Form Two Congruent Triangles: Each diagonal divides the rectangle into two right-angled triangles that are identical in size and shape.
4. Not Perpendicular: Unlike squares, the diagonals of a rectangle are not perpendicular (they don't form right angles where they cross), unless the rectangle is a square.
Remember
The diagonals of a rectangle are equal and bisect each other, but they are not perpendicular unless it's a square.
Diagonal Formulas
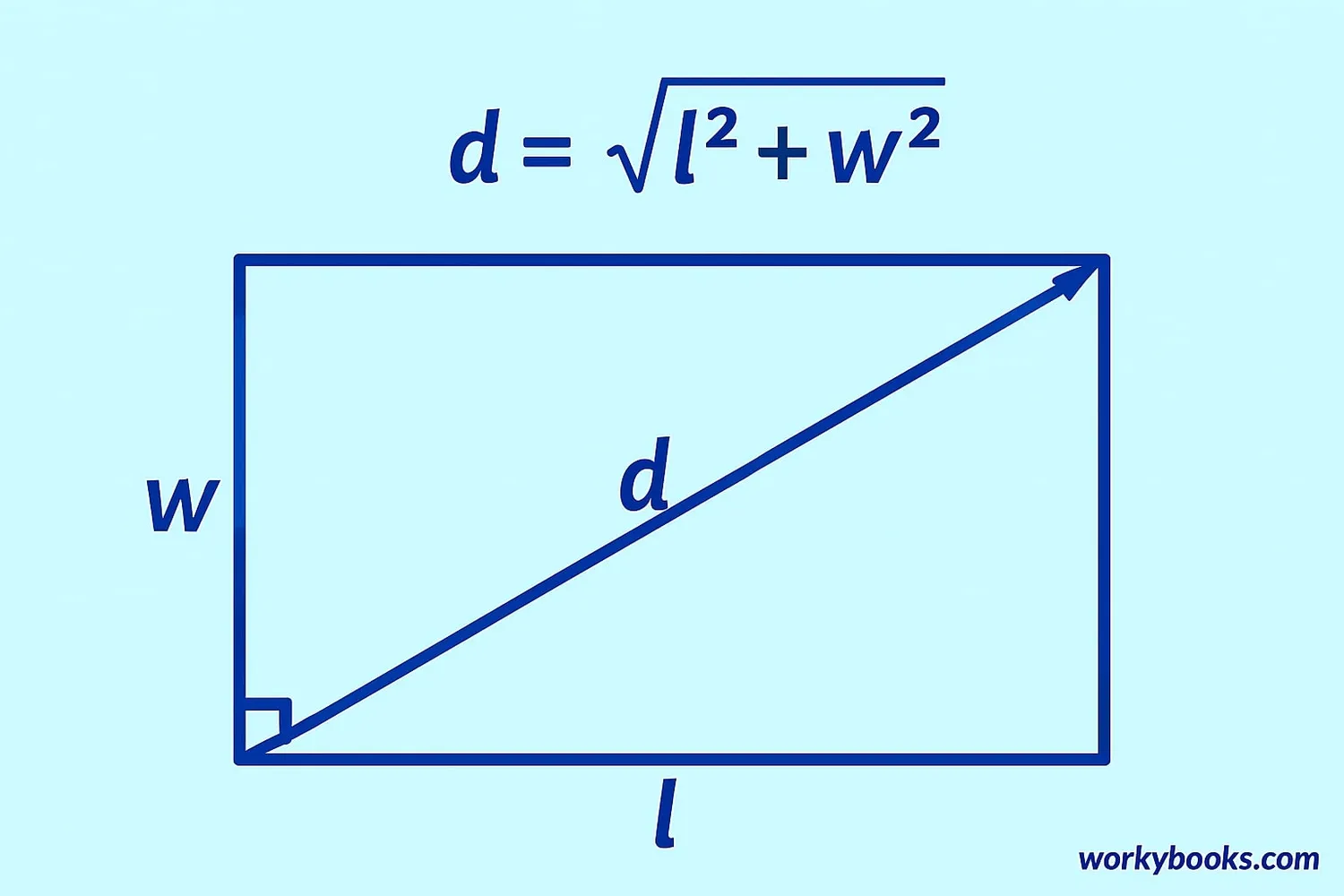
We can calculate the length of a diagonal using the Pythagorean Theorem. If we know the length (l) and width (w) of a rectangle, we can find the diagonal (d) with this formula:
Diagonal Formula
Where:
d = diagonal length
l = length of the rectangle
w = width of the rectangle
This formula comes from the Pythagorean Theorem, which says that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Since the diagonal divides the rectangle into two right-angled triangles, we can use this theorem to find its length.
Related Formulas
Area of rectangle = length × width
Perimeter of rectangle = 2 × (length + width)
Examples and Practice
Let's practice finding diagonals with some examples:
Example 1: A rectangle has length 3 cm and width 4 cm. What is the length of its diagonal?
Solution: d = √(3² + 4²) = √(9 + 16) = √25 = 5 cm
Example 2: A soccer field is 100 meters long and 60 meters wide. How long is the diagonal?
Solution: d = √(100² + 60²) = √(10000 + 3600) = √13600 ≈ 116.62 meters
Example 3: The diagonal of a rectangle is 13 inches, and its width is 5 inches. What is its length?
Solution: Using the formula: 13 = √(l² + 5²) → 169 = l² + 25 → l² = 144 → l = 12 inches
Practice Table
| Length | Width | Diagonal |
|---|---|---|
| 6 cm | 8 cm | √(6² + 8²) = 10 cm |
| 9 in | 12 in | √(9² + 12²) = 15 in |
| 5 m | 12 m | √(5² + 12²) = 13 m |
| 7 ft | 24 ft | √(7² + 24²) = 25 ft |
Pattern Notice
These examples form Pythagorean triples! The sides and diagonal are all whole numbers that satisfy the Pythagorean theorem.
Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about rectangle diagonals:
Geometry Trivia
Discover interesting facts about rectangles and diagonals:
Ancient Origins
The word "rectangle" comes from the Latin "rectangulus", meaning "right-angled". Rectangles have been studied since ancient Egyptian and Babylonian times for land measurement.
Golden Rectangle
A special rectangle called the "Golden Rectangle" has sides in the ratio 1:1.618. Its diagonal and sides create interesting mathematical relationships found in nature and art.
3D Diagonals
In 3D space, a rectangular prism has four space diagonals (connecting opposite vertices through the interior). The formula for their length is √(l² + w² + h²).
Largest Rectangle
The largest rectangular flag ever flown was in Romania in 2013, measuring 349.4 m × 226.9 m (1,146 ft × 744 ft). Its diagonal would be over 400 meters long!





