Factoring Polynomials - Definition, Examples, Quiz, FAQ, Trivia
Learn to break down polynomials into simpler parts with easy explanations and practice activities
What is Factoring Polynomials?
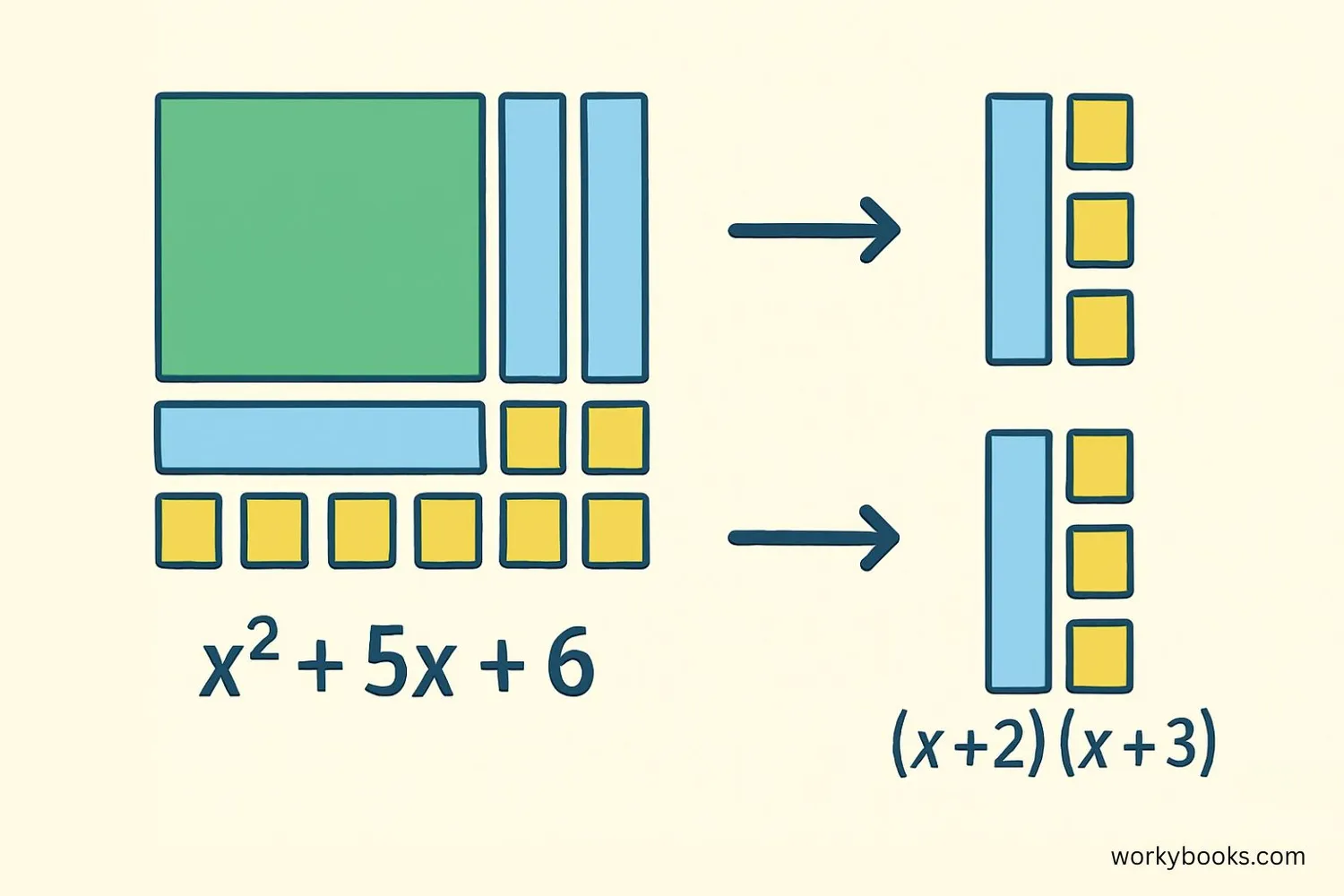
Factoring polynomials is like breaking down a large number into its multiplication components. For example, the number 12 can be broken down into 3 × 4 or 2 × 6. Similarly, polynomials can be broken down into simpler polynomial factors.
A polynomial is an expression with variables, coefficients, and exponents. For example, x² + 5x + 6 is a polynomial. Factoring helps us simplify these expressions and solve equations more easily.
When we factor a polynomial, we're looking for simpler expressions that multiply together to give us the original polynomial. This is especially useful for finding the roots or solutions to polynomial equations.
Key Concept
Factoring is the reverse process of multiplying polynomials. If (x+2)(x+3) = x²+5x+6, then factoring x²+5x+6 gives us (x+2)(x+3).
How to Factor Polynomials
There are several methods for factoring polynomials. Let's look at the most common ones:
1. Greatest Common Factor (GCF)
The first step in factoring is always to look for a common factor in all terms.
2 Factor out the GCF
3 Write the remaining polynomial in parentheses
Example: Factor 4x³ + 8x²
The GCF is 4x²
Factored form: 4x²(x + 2)
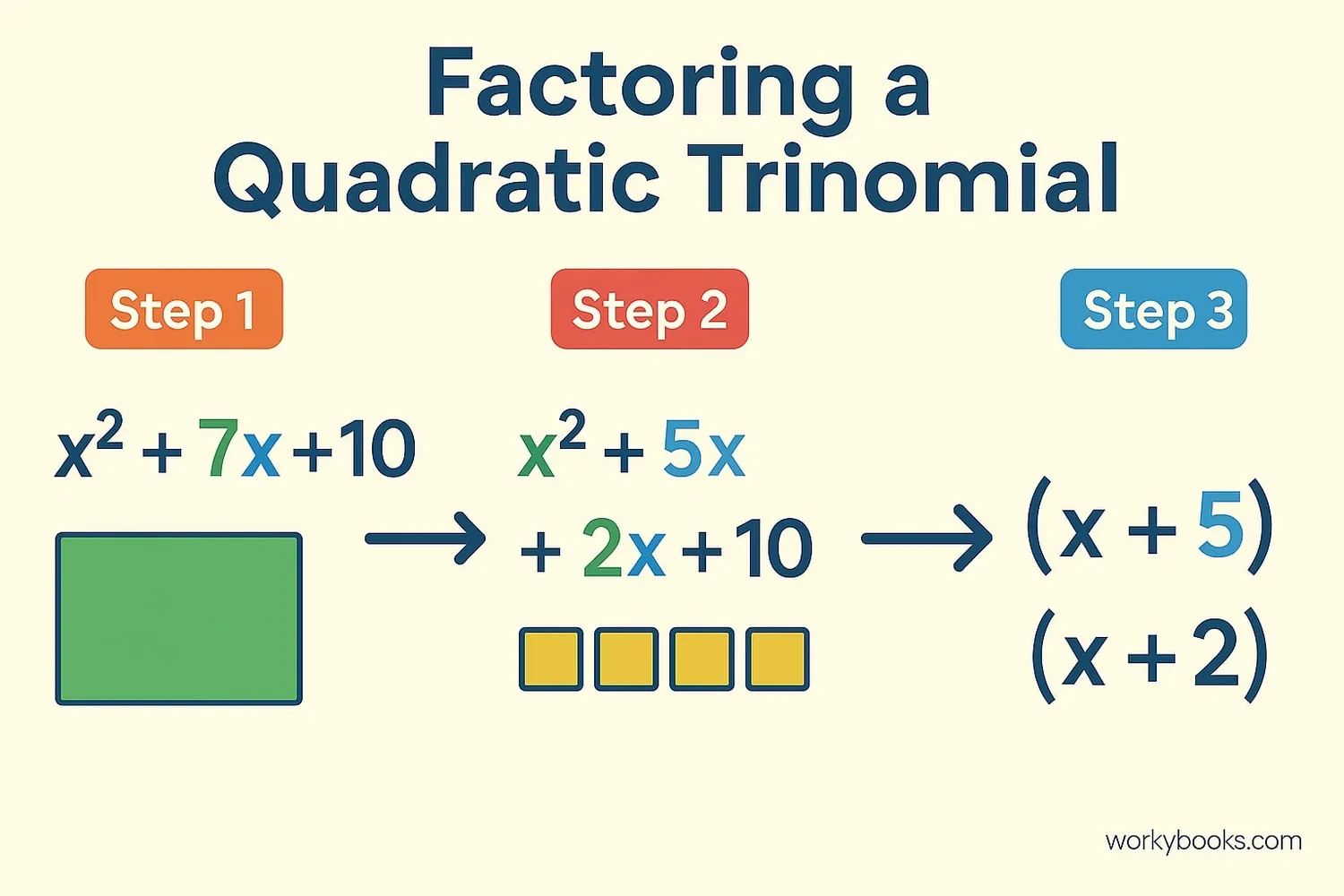
2. Factoring Quadratic Trinomials
For expressions like ax² + bx + c, we look for two numbers that multiply to give 'ac' and add to give 'b'.
2 Find two numbers that multiply to 'ac' and add to 'b'
3 Rewrite the middle term using these numbers
4 Factor by grouping
Remember
Always check your factoring by multiplying the factors back together. You should get the original polynomial!
Factoring Examples

Let's look at some examples of factoring polynomials:
Example 1: Factoring with GCF
Factor: 6x⁴ - 9x³ + 3x²
Step 1: Find the GCF of all terms → 3x²
Step 2: Divide each term by the GCF → (6x⁴/3x²) - (9x³/3x²) + (3x²/3x²)
Step 3: Write as product → 3x²(2x² - 3x + 1)
Example 2: Factoring Quadratic Trinomials
Factor: x² + 7x + 12
Step 1: Find two numbers that multiply to 12 and add to 7 → 3 and 4
Step 2: Write as product → (x + 3)(x + 4)
Check: (x + 3)(x + 4) = x² + 4x + 3x + 12 = x² + 7x + 12 ✓
Example 3: Factoring Difference of Squares
Factor: x² - 25
This is a difference of squares: a² - b² = (a + b)(a - b)
So: x² - 25 = x² - 5² = (x + 5)(x - 5)
Practice Tip
The more you practice different types of factoring problems, the easier it becomes to recognize which method to use.
Factoring Practice Quiz
Test your factoring skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about factoring polynomials:
Math Trivia
Discover interesting facts about polynomials and algebra:
Ancient Origins
The word "algebra" comes from the Arabic word "al-jabr" which means "reunion of broken parts." This term was used in the title of a book by the Persian mathematician Al-Khwarizmi around 820 AD.
Polynomial Degrees
The degree of a polynomial is the highest exponent of its variable. Polynomials are used to model many real-world situations, from the path of a thrown ball to population growth patterns.
Applications in Science
Factoring polynomials is essential in physics for solving equations of motion, in engineering for designing structures, and in computer science for creating algorithms and cryptography systems.
The Fundamental Theorem
The Fundamental Theorem of Algebra states that every polynomial equation of degree n has exactly n roots (solutions), though some may be complex numbers. This was first proven by Carl Friedrich Gauss in 1799.





