Factors of 72 - Definition, Examples, Quiz, FAQ, Trivia
Learn how to find all factors of 72 with easy explanations, visual examples, and practice activities
What are Factors?

Factors are numbers we multiply together to get another number. For example, the factors of 72 are numbers that multiply in pairs to give 72.
Think of factors like best friends that work together to create a number. If you have 72 cookies and want to share them equally, factors tell you how many friends could get the same amount with no cookies left over!
Some key facts about factors:
- Every number has at least two factors: 1 and itself
- Factors are always whole numbers (no fractions)
- 72 is a composite number because it has more than two factors
Key Concept
A factor of a number divides it exactly with no remainder. For 72, if 72 ÷ number gives a whole number, then that number is a factor.
Finding Factors of 72

Let's find all factors of 72 using division:
- Start with 1: 72 ÷ 1 = 72, so 1 and 72 are factors
- Try 2: 72 ÷ 2 = 36, so 2 and 36 are factors
- Try 3: 72 ÷ 3 = 24, so 3 and 24 are factors
- Try 4: 72 ÷ 4 = 18, so 4 and 18 are factors
- Try 6: 72 ÷ 6 = 12, so 6 and 12 are factors
- Try 8: 72 ÷ 8 = 9, so 8 and 9 are factors
- Continue until you reach the middle
Remember
Factors come in pairs! When you find one factor, you automatically find its partner.
Prime Factorization of 72
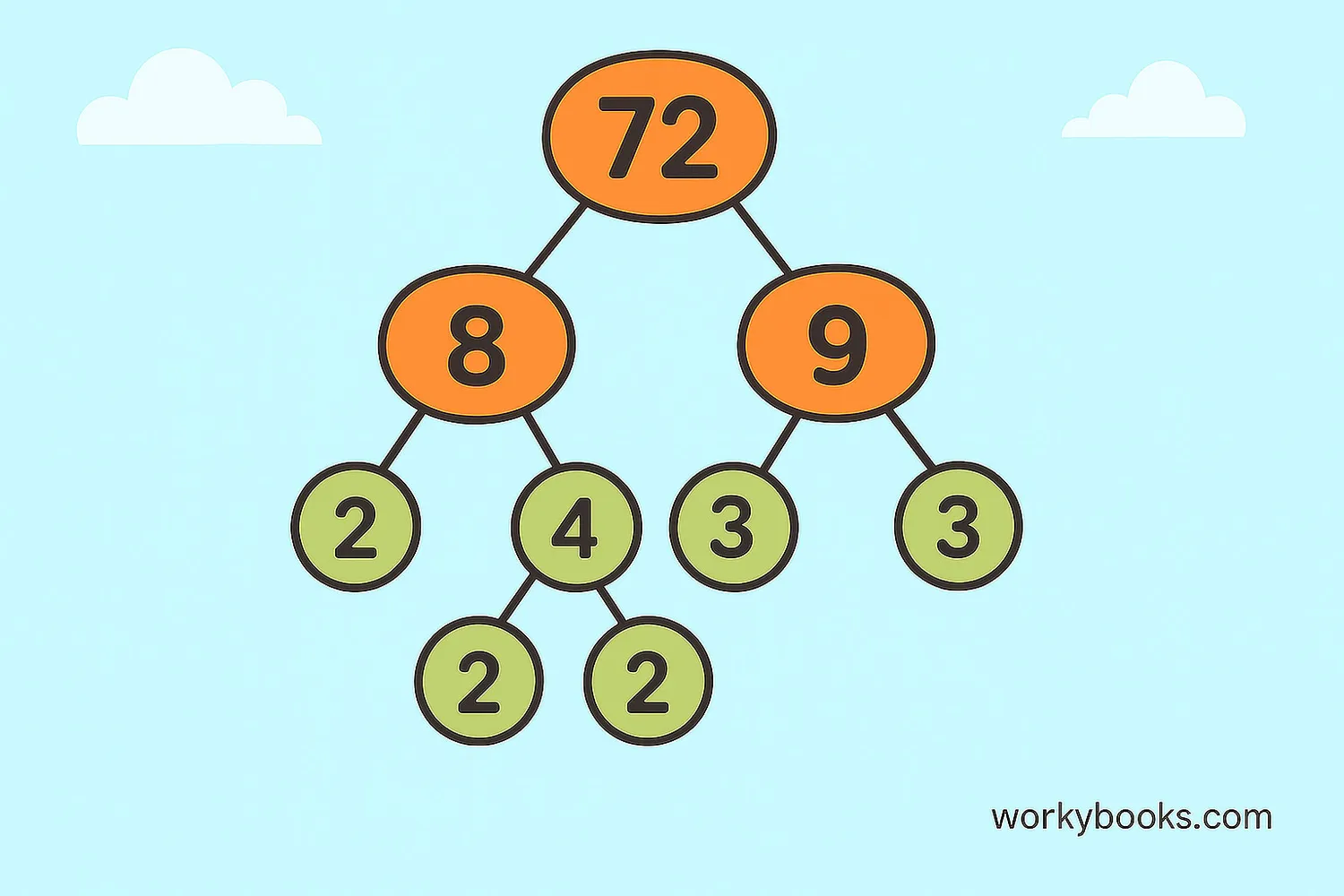
Prime factorization means breaking down a number into its smallest prime factors. Prime numbers are numbers greater than 1 that have only two factors: 1 and themselves.
We can use a factor tree to find the prime factors of 72:
This shows that 72 = 2 × 2 × 2 × 3 × 3. We can write this using exponents: 72 = 2³ × 3².
The prime factors of 72 are 2 and 3. The fundamental theorem of arithmetic tells us that every number has a unique prime factorization!
Prime Factorization
Factor Pairs of 72
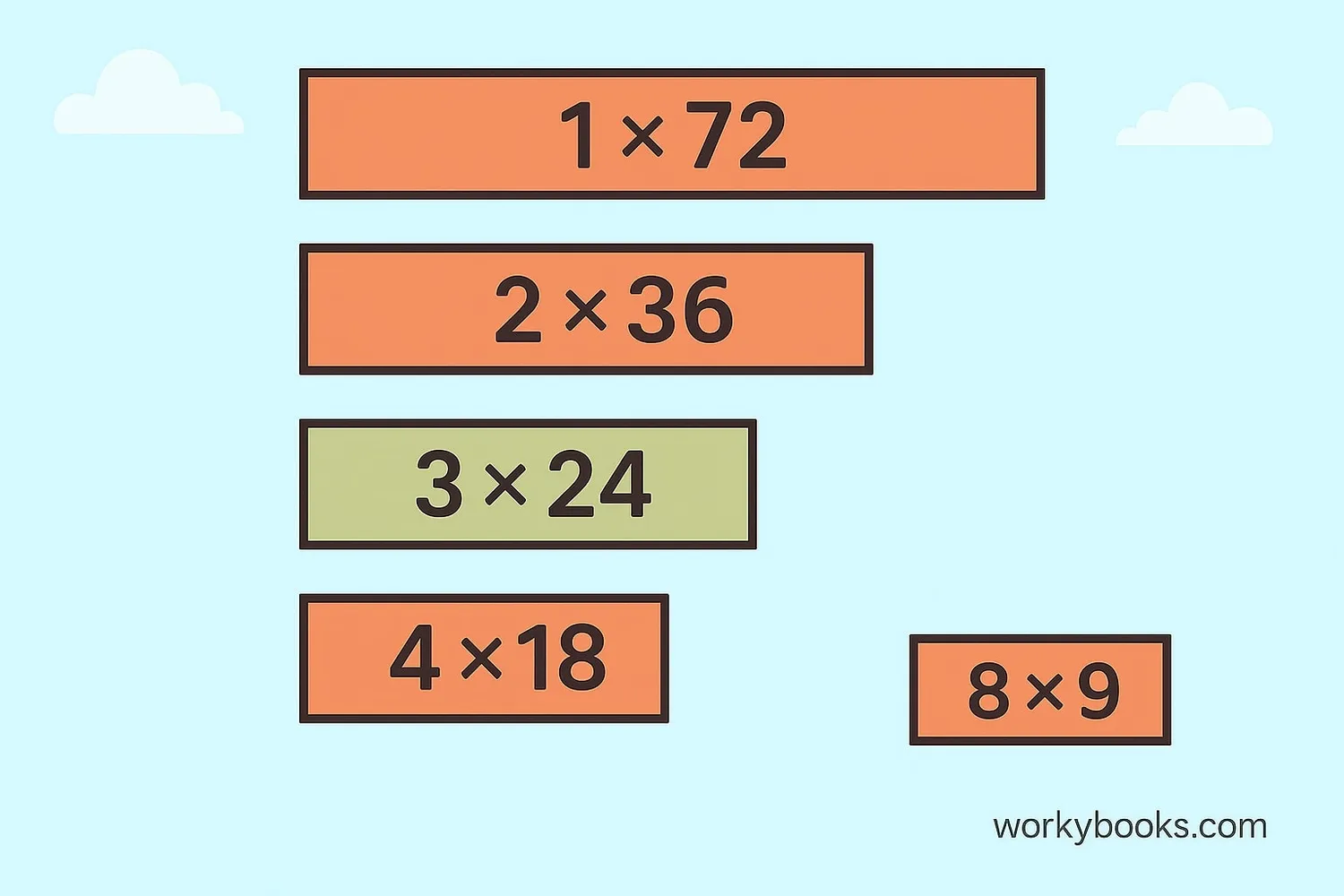
Factor pairs are two numbers that multiply together to give the original number. For 72, we have both positive and negative factor pairs.
Positive factor pairs of 72:
Pair 1
Pair 2
Pair 3
Pair 4
Pair 5
Pair 6
Negative factor pairs work the same way but with negative numbers:
(-1 × -72), (-2 × -36), (-3 × -24), etc.
Notice that the pairs are the same as the positive pairs, just with negative signs!
Remember
When multiplying two negative numbers, the result is positive. That's why negative factor pairs also multiply to 72.
Real-World Examples

Let's see how factors of 72 work in real life:
Example 1: Ms. Johnson has 72 students. She wants to divide them into equal groups for a project. How many students could be in each group?
Solution: Using factors, she could make groups of 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, or 72 students.
Example 2: A baker has 72 cookies to arrange on trays. Each tray must hold the same number of cookies. What are possible arrangements?
Solution: She could use 8 trays with 9 cookies each (8×9=72), or 6 trays with 12 cookies each (6×12=72), or other factor pair arrangements.
Example 3: A rectangular garden has an area of 72 square feet. What could its dimensions be?
Solution: The length and width would be factor pairs: 1ft×72ft, 2ft×36ft, 3ft×24ft, 4ft×18ft, 6ft×12ft, or 8ft×9ft.
Math Tip
Factors help us solve problems about equal sharing, arranging objects, and finding dimensions of rectangles.
Factors of 72 Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about factors of 72:
Number Trivia
Discover interesting facts about numbers and factors:
Ancient Number Systems
The concept of factors dates back to ancient Greek mathematicians. Euclid's "Elements" written around 300 BC contains fundamental theorems about factors and prime numbers.
Highly Composite Numbers
72 is a highly composite number because it has more factors than any smaller number. The numbers before 72 with many factors are 60 (12 factors) and 48 (10 factors).
Factors in Nature
Factors appear in nature! Bees build honeycombs with hexagonal cells because this shape allows them to store the most honey using the least wax, and 6 is a factor of 72.
The Number 72
72 appears in many places: there are 72 degrees between compass points in some navigation systems, and in astronomy, the sun moves 1 degree every 72 years relative to the stars.





