Hypotenuse in Right Triangles - Definition, Examples, Quiz, FAQ, Trivia
Learn about the longest side of a right triangle with easy explanations and practice activities
What is a Hypotenuse?
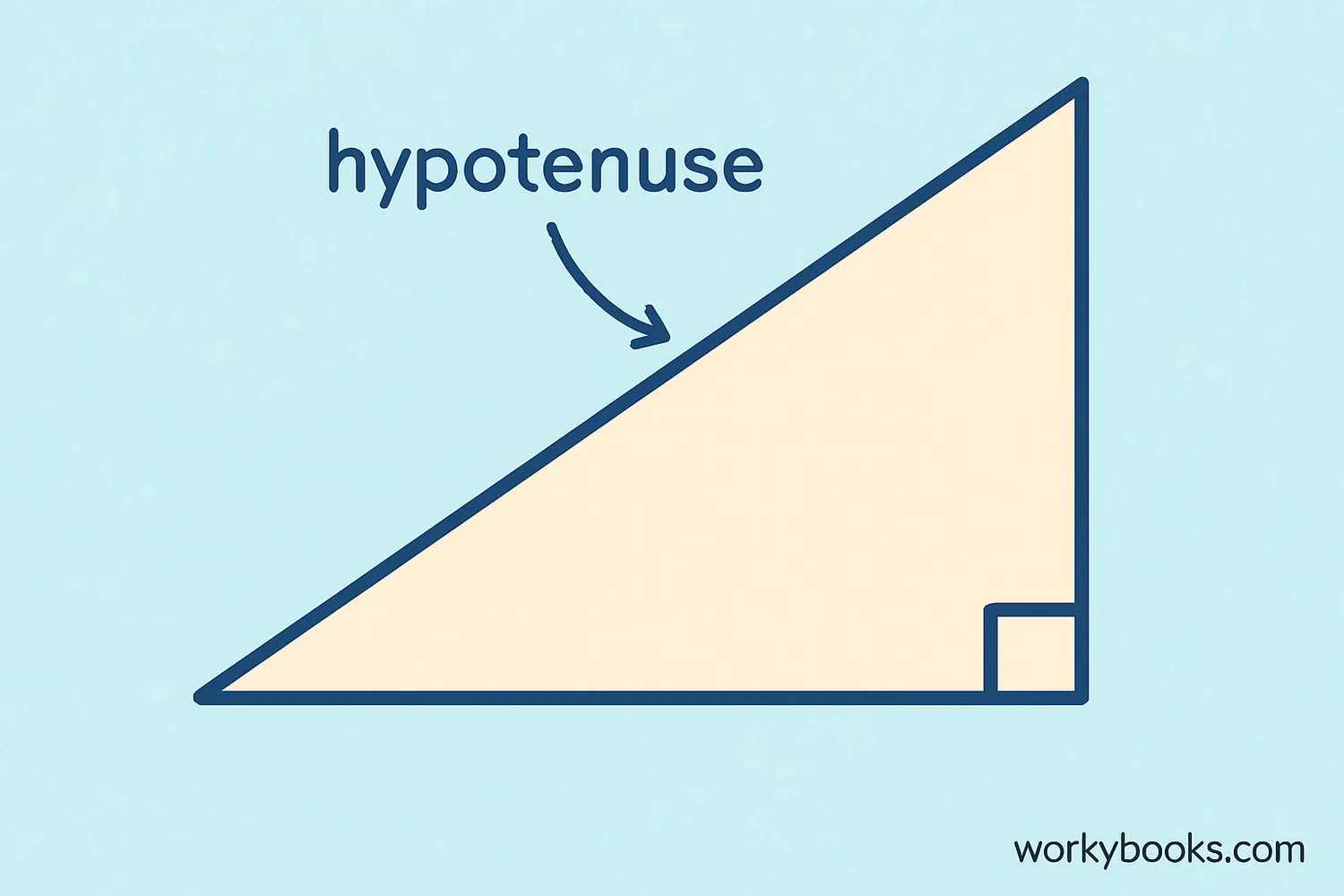
The hypotenuse is the longest side of a right triangle. It's always located opposite the right angle (the 90-degree angle). In any right triangle, the hypotenuse has special properties that make it important in geometry.
Why is the hypotenuse special? It's not just the longest side - it also has a special relationship with the other two sides, called the Pythagorean theorem. This relationship helps us calculate the length of the hypotenuse when we know the lengths of the other two sides.
The word "hypotenuse" comes from the Greek word "hypoteinousa," which means "stretching under" or "subtending." This makes sense because the hypotenuse "stretches under" the right angle in a right triangle.
Key Concept
The hypotenuse is always the side opposite the right angle in a right triangle and is always the longest side.
The Pythagorean Theorem
The Pythagorean theorem is a fundamental rule in geometry that describes the relationship between the three sides of a right triangle. It states that:
Pythagorean Theorem
Where a and b are the lengths of the two legs, and c is the length of the hypotenuse.
The Pythagorean theorem is named after the ancient Greek mathematician Pythagoras, although evidence suggests the relationship was known to Babylonian mathematicians even earlier.
Remember
The Pythagorean theorem only works for right triangles. It doesn't apply to other types of triangles.
How to Find the Hypotenuse
Finding the length of the hypotenuse is straightforward when you know the lengths of the other two sides. Here's the step-by-step process:
Step 1: Identify the lengths of the two legs (the sides that form the right angle). Let's call them a and b.
Step 2: Square both lengths (multiply each by itself).
Step 3: Add the two squares together.
Step 4: Take the square root of the sum.
This gives you the length of the hypotenuse!
Let's try an example: If one leg is 3 units long and the other is 4 units long:
3² = 9, 4² = 16
9 + 16 = 25
√25 = 5
So the hypotenuse is 5 units long.
Calculation Tip
Remember to always take the square root at the end. Many students forget this final step!
Real-World Examples
The hypotenuse concept appears in many real-world situations. Here are some examples:
Example 1: A ladder leaning against a wall forms a right triangle. If the base of the ladder is 3 meters from the wall and reaches 4 meters up the wall, how long is the ladder?
Solution: 3² + 4² = 9 + 16 = 25, √25 = 5. The ladder is 5 meters long.
Example 2: You're walking through a park. Instead of walking along two perpendicular paths that are 300 meters and 400 meters long, you can walk diagonally. How much shorter is the diagonal path?
Solution: The diagonal is the hypotenuse: √(300² + 400²) = √(90,000 + 160,000) = √250,000 = 500 meters. The two paths total 700 meters, so the diagonal saves 200 meters.
Example 3: A television screen is measured diagonally. If a TV is 24 inches wide and 18 inches tall, what is its diagonal measurement?
Solution: √(24² + 18²) = √(576 + 324) = √900 = 30 inches.
These examples show how the hypotenuse concept helps solve practical problems in construction, navigation, and everyday life.
Real-World Connection
The diagonal measurement of TV and computer screens is actually the hypotenuse of a right triangle formed by the width and height!
Hypotenuse Practice Quiz
Test your understanding of the hypotenuse with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the hypotenuse:
Geometry Trivia
Discover interesting facts about triangles and the Pythagorean theorem:
Ancient Knowledge
The Pythagorean theorem was known to Babylonian mathematicians over 1000 years before Pythagoras was born! A Babylonian tablet from around 1800 BCE shows the relationship between the sides of a right triangle.
Pythagorean Triples
Pythagorean triples are sets of three positive integers that satisfy the Pythagorean theorem, like 3-4-5, 5-12-13, and 7-24-25. These triples were used by ancient surveyors and builders to create perfect right angles.
Space Measurements
NASA scientists use the Pythagorean theorem to calculate distances in space. For example, they might use it to determine how far a spacecraft is from a planet or to calculate trajectories between celestial bodies.
The Longest Hypotenuse
The largest right triangle ever mathematically described would have a hypotenuse longer than the observable universe! While this is theoretical, it shows how the Pythagorean theorem works at any scale.





