Isosceles Right Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn about special right triangles with two equal sides and one right angle
What is an Isosceles Right Triangle?

An isosceles right triangle is a special type of triangle that has two important features:
1. It has one right angle (90 degrees)
2. It has two equal sides (legs)
Because it has a right angle and two equal sides, it's called an "isosceles right triangle." You might also hear it called a 45-45-90 triangle because its angles are always 45°, 45°, and 90°.
These triangles are special because they have predictable relationships between their sides, which makes calculations easier!
Key Concept
In an isosceles right triangle, the two acute angles are always equal (each 45°), and the sides opposite these angles are also equal.
Properties of Isosceles Right Triangles
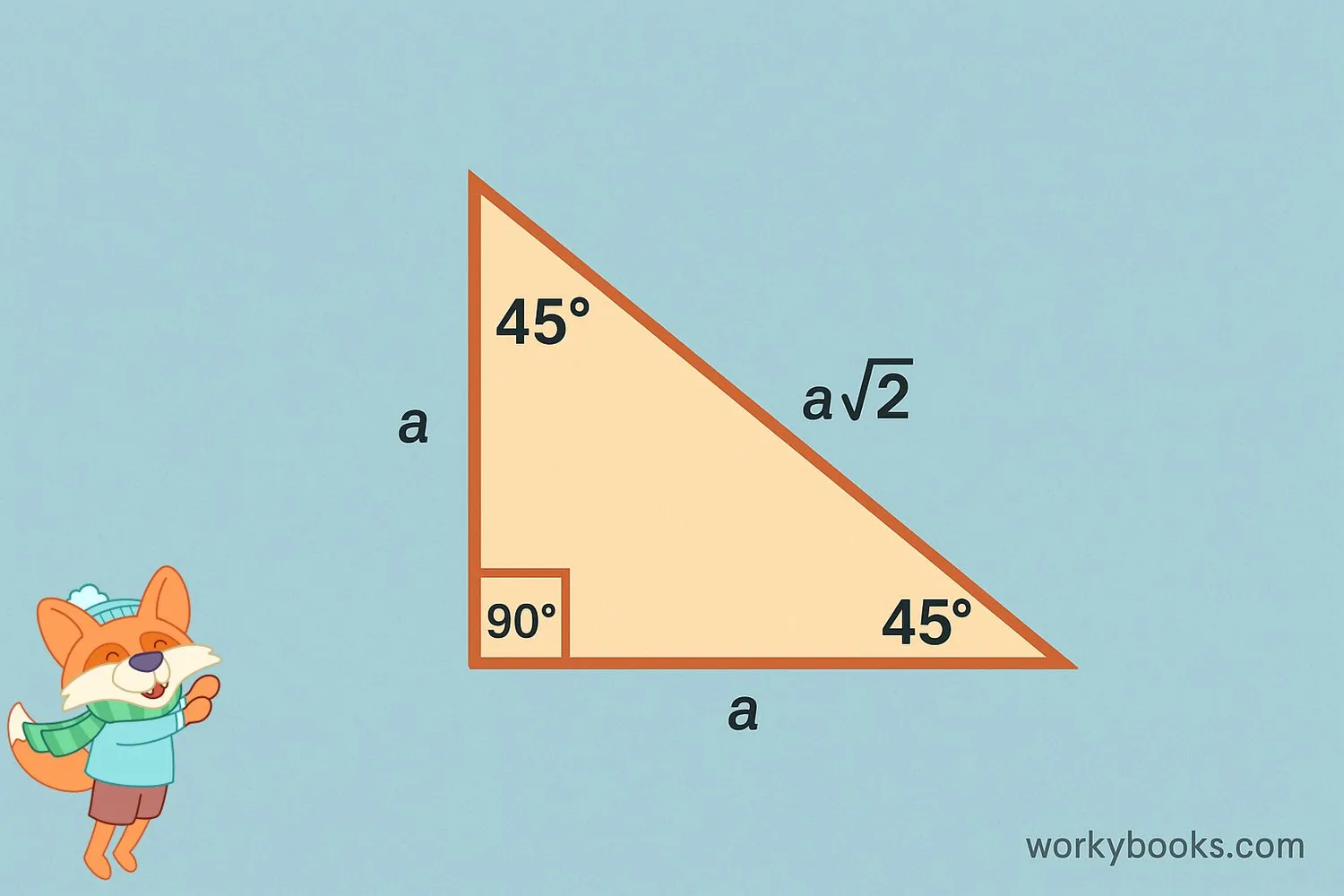
Isosceles right triangles have special properties that make them different from other triangles:
- One angle is exactly 90° (a right angle)
- The two legs (the sides that form the right angle) are equal in length
- The two acute angles are each 45°
- The hypotenuse (the side opposite the right angle) is longer than either leg
- The hypotenuse equals the leg length multiplied by √2 (approximately 1.414)
- It has reflection symmetry across the line that bisects the right angle
Remember
If you know the length of one leg in an isosceles right triangle, you can find all other measurements using the special properties!
Formulas for Isosceles Right Triangles
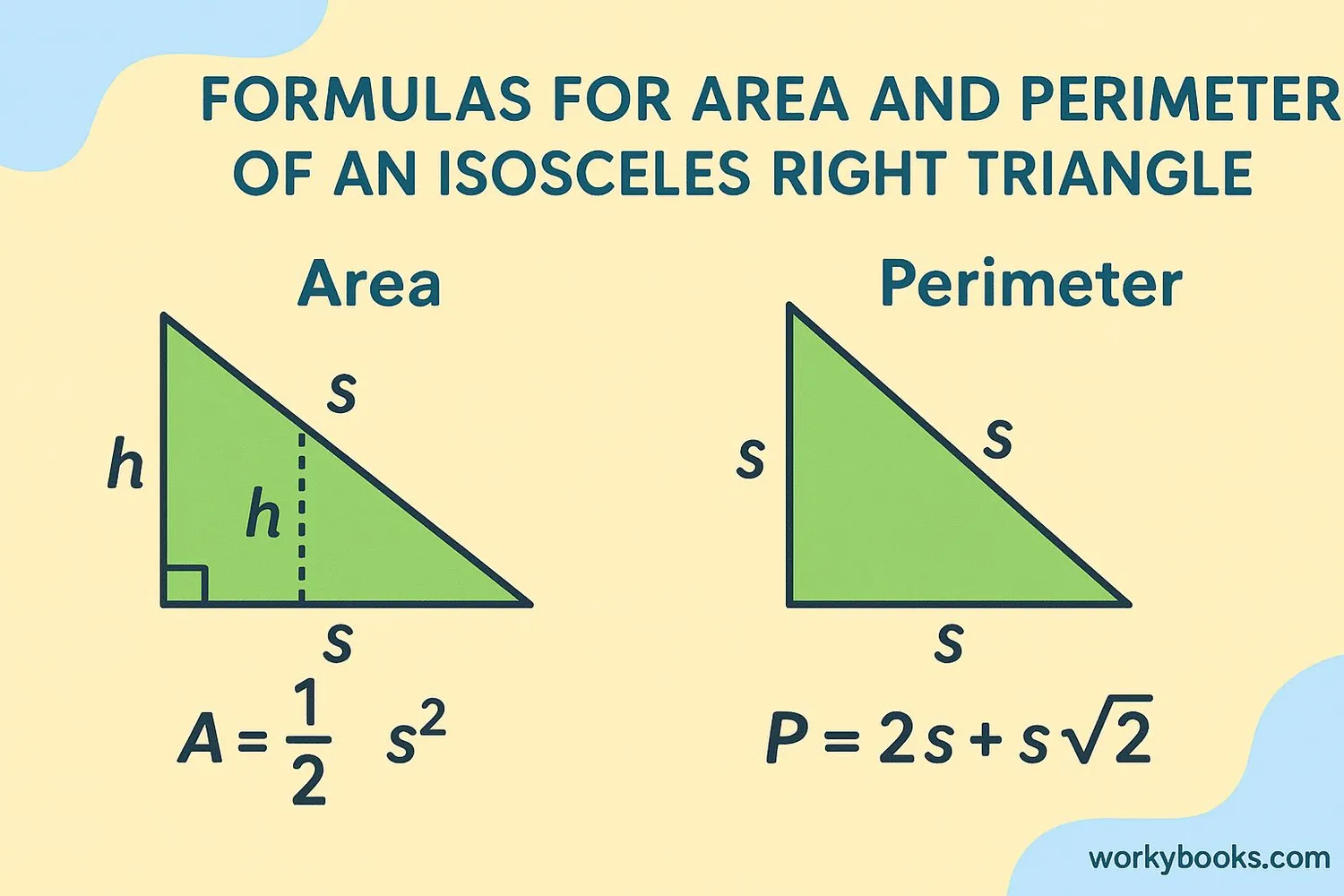
Because isosceles right triangles have special properties, we have special formulas to calculate their measurements:
Hypotenuse Formula
Where 'a' is the length of each equal side, and 'c' is the hypotenuse
Area Formula
Where 'a' is the length of each equal side
Perimeter Formula
Where 'a' is the length of each equal side
Remember that √2 is approximately 1.414. So if each leg is 5 cm long:
Hypotenuse = 5 × 1.414 ≈ 7.07 cm
Area = ½ × 5² = ½ × 25 = 12.5 cm²
Perimeter = 5 + 5 + 7.07 = 17.07 cm
Real-World Examples

Isosceles right triangles appear in many real-world situations. Let's look at some examples:
Example 1: A set square (a tool used in drafting) often has the shape of an isosceles right triangle with two equal sides of 10 cm. What is the length of its hypotenuse?
Solution: Hypotenuse = 10 × √2 ≈ 10 × 1.414 = 14.14 cm
Example 2: A quilt pattern uses isosceles right triangles with legs measuring 6 inches each. What is the area of each triangle?
Solution: Area = ½ × 6² = ½ × 36 = 18 square inches
Example 3: A diagonal cross brace in a gate forms two isosceles right triangles. If the gate is 4 feet wide and 4 feet tall, how long is the brace?
Solution: The brace is the hypotenuse of a triangle with legs of 4 feet each.
Hypotenuse = 4 × √2 ≈ 4 × 1.414 = 5.656 feet
Example 4: A sandwich is cut diagonally, creating two isosceles right triangles. If the sandwich was 8 cm on each side, what is the perimeter of one triangle?
Solution: Each triangle has two legs of 8 cm each, and a hypotenuse of 8 × √2 ≈ 11.31 cm
Perimeter = 8 + 8 + 11.31 = 27.31 cm
Real-World Connection
Look around you—can you spot any isosceles right triangles? They're often found in construction, art, and everyday objects!
Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about isosceles right triangles:
Triangle Trivia
Discover interesting facts about triangles and geometry:
Ancient Discovery
The properties of isosceles right triangles were known to ancient Egyptians, who used them in building the pyramids. They used knotted ropes to create perfect right angles for construction.
Irrational Numbers
The hypotenuse of an isosceles right triangle with legs of length 1 is √2, which was the first irrational number discovered by the ancient Greeks. This discovery was initially kept secret as it challenged their belief that all numbers were rational.
Architectural Stability
Isosceles right triangles are often used in architecture and engineering because they provide excellent stability. The Eiffel Tower's design incorporates many triangular elements that provide strength while using minimal material.
Art and Design
Isosceles right triangles appear frequently in art and design. The famous artist Piet Mondrian used geometric shapes including right triangles in his abstract compositions, creating balanced and harmonious works.





