Negative Slope - Definition, Examples, Quiz, FAQ, Trivia
Learn about downward-sloping lines in math with visual examples and practice activities
What is Negative Slope?
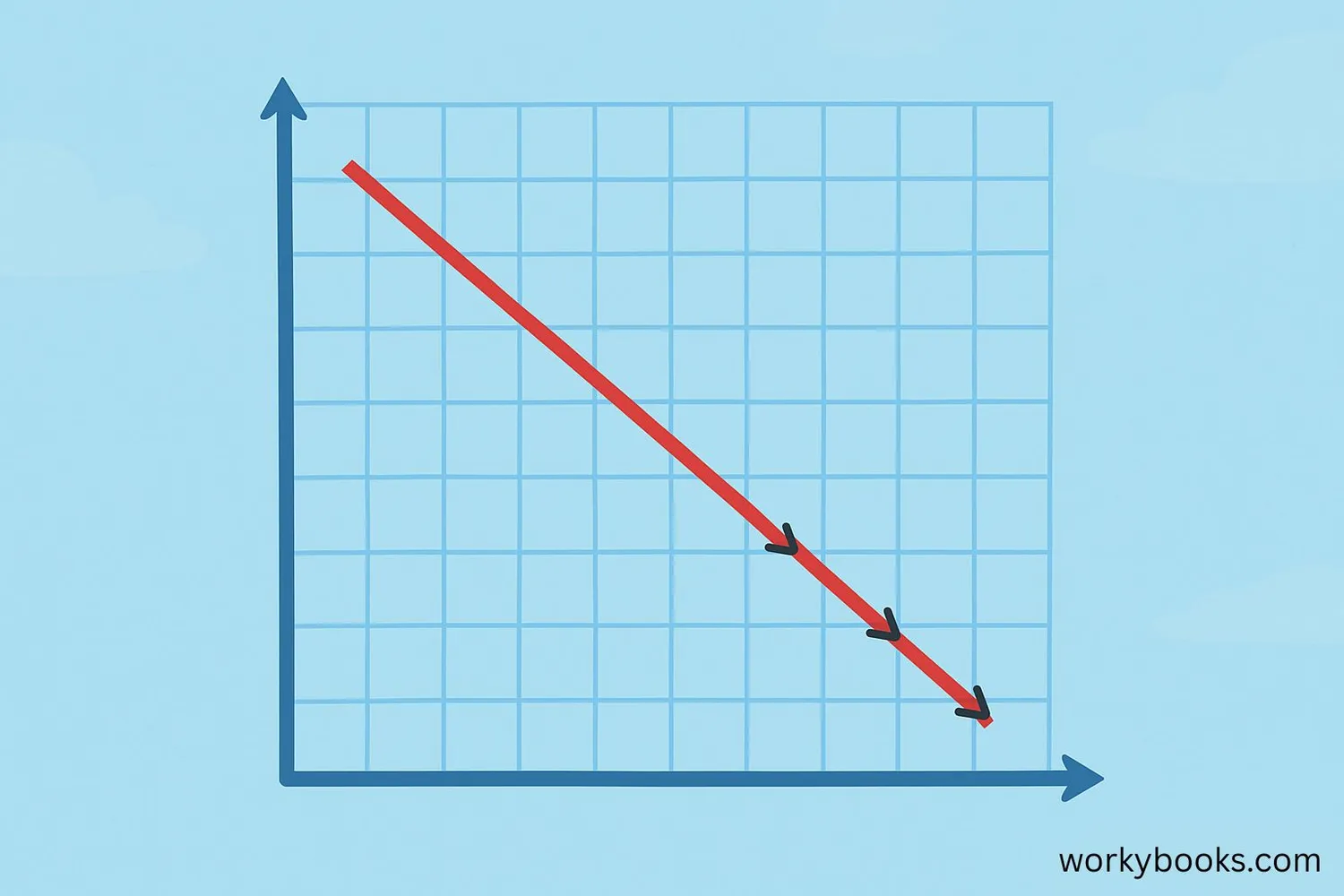
Slope tells us how steep a line is and in which direction it goes. A negative slope means that as you move from left to right along a line, the line goes downhill.
Think of a slide at the playground - when you slide down, that's like a negative slope! In math, we use the letter "m" to represent slope. When you see a negative sign before the slope value (like m = -2), you know the line is going downhill.
Key things to remember about negative slope:
- It decreases as you move from left to right
- The line goes downward from left to right
- It's represented by a negative number
Key Concept
A negative slope means the line decreases as you move from left to right on the graph. It's like going downhill.
Calculating Negative Slope
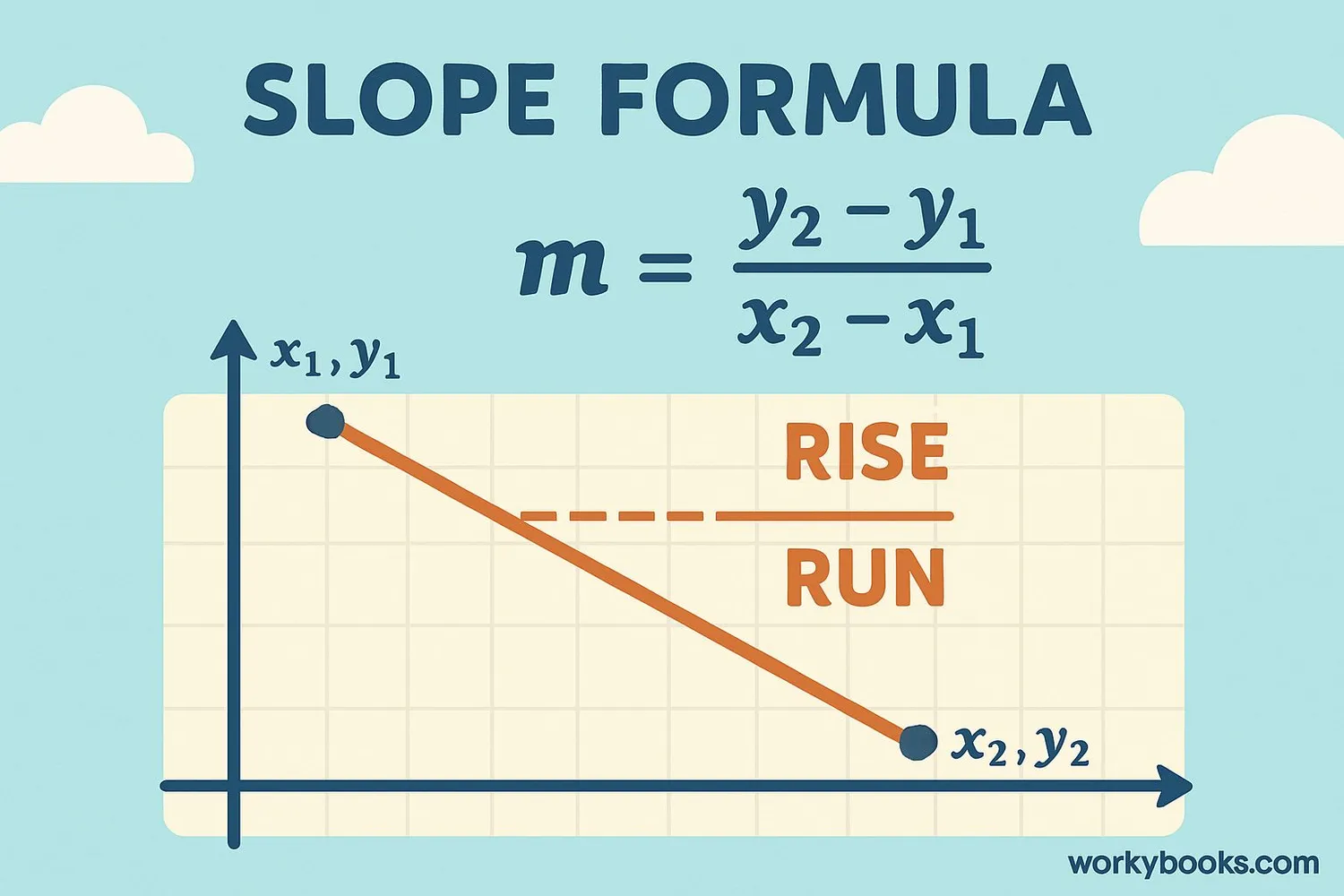
To calculate slope, we use the formula:
Slope Formula
Slope = Rise ÷ Run
Example: Calculate the slope between points (1, 5) and (3, 1)
Step 1: Identify coordinates → Point A (1, 5), Point B (3, 1)
Step 2: Calculate rise (change in y) → 1 - 5 = -4
Step 3: Calculate run (change in x) → 3 - 1 = 2
Step 4: Slope = rise/run → -4 ÷ 2 = -2
So the slope is -2, which is negative. This means for every 2 units you move right, you move down 4 units.
Remember
Negative slope means the line is decreasing. The numerator (rise) in the slope formula will be negative when you calculate from left to right.
Graphing Negative Slope
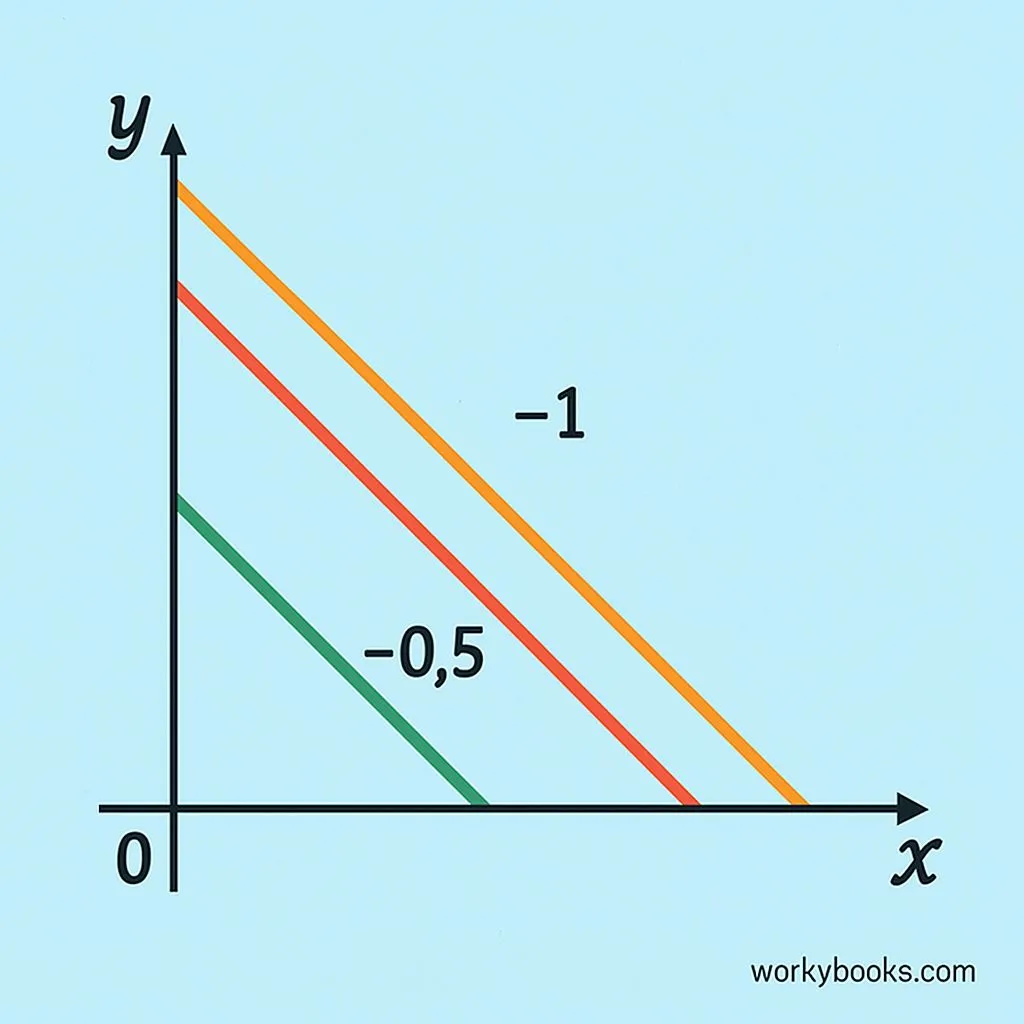
When graphing a line with negative slope:
- Start at the y-intercept (where the line crosses the y-axis)
- Use the slope to find another point
- Since slope is negative, move down for rise and right for run
- Connect the points to draw the line
- A slope of -1 means a 45° downward angle
- A slope of -2 is steeper (goes down faster)
- A slope of -0.5 is less steep (goes down slowly)
Negative vs Positive Slope
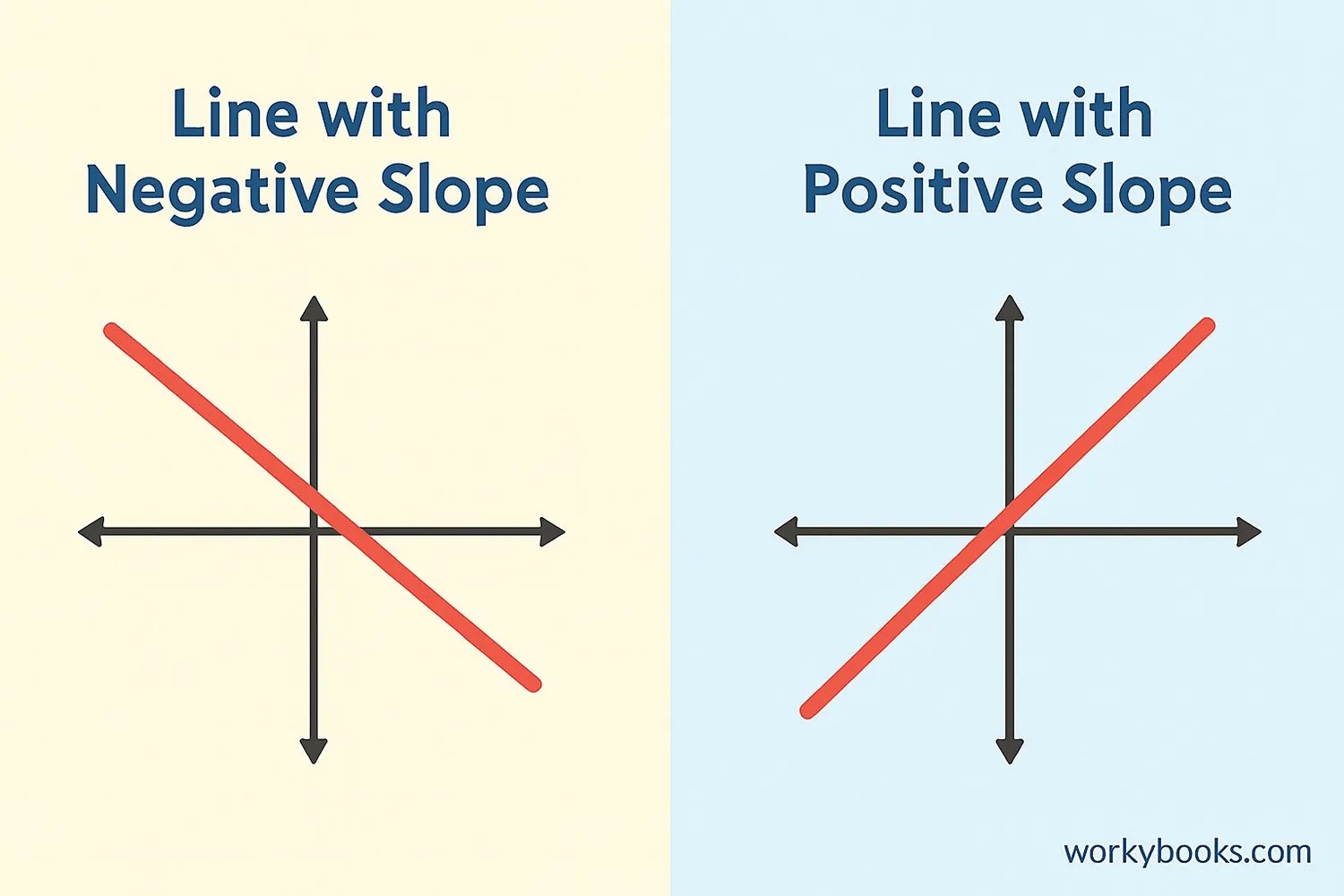
Understanding the difference between negative and positive slope helps in recognizing line directions:
| Feature | Negative Slope | Positive Slope |
|---|---|---|
| Direction | Downhill (decreasing) | Uphill (increasing) |
| Slope Value | Negative number | Positive number |
| Movement | Down as you move right | Up as you move right |
| Graph Example | Top-left to bottom-right | Bottom-left to top-right |
| Real-World Example | Slide going down | Stairs going up |
Quick Tip
Remember: Negative slope = downhill, Positive slope = uphill!
Real-World Examples
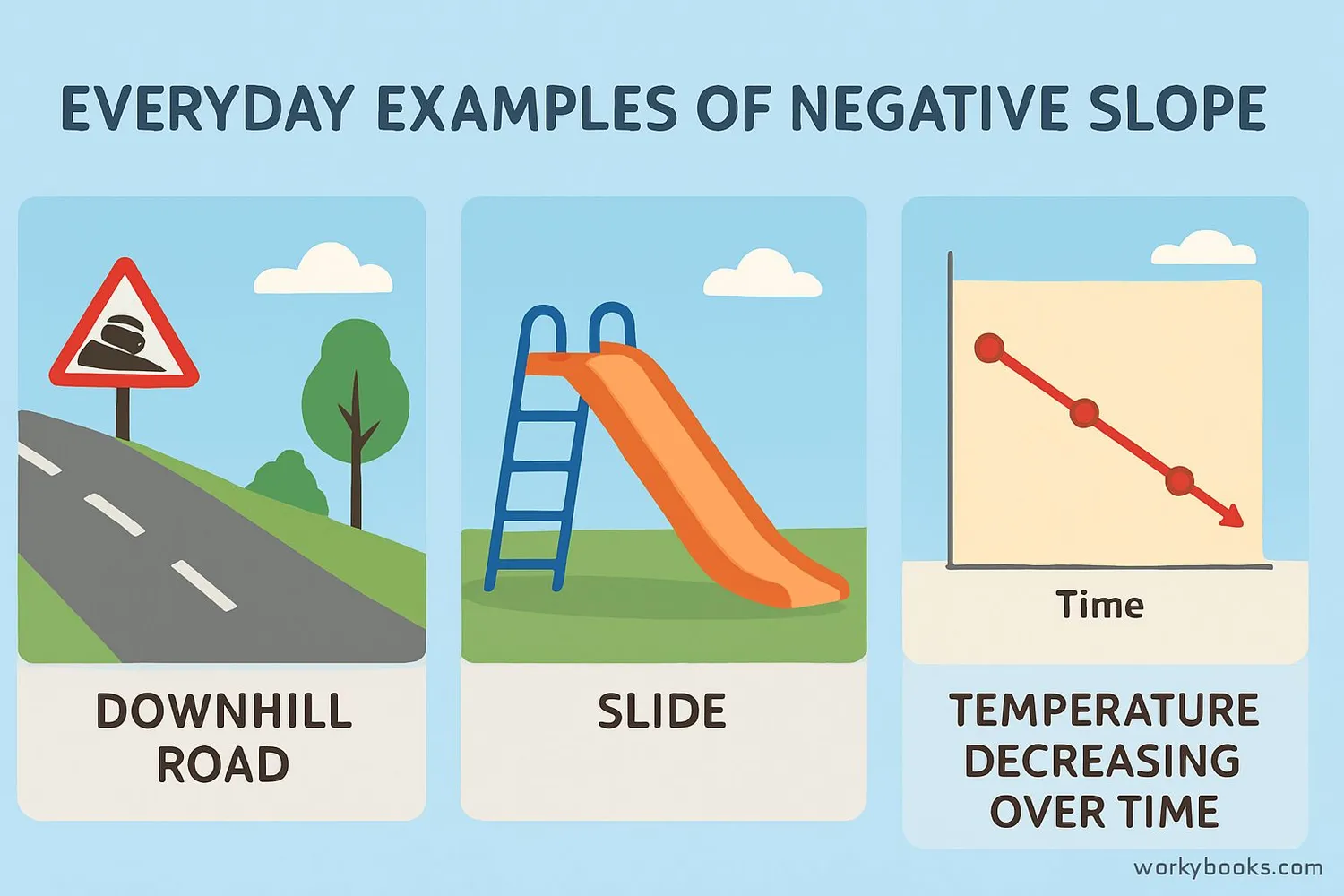
Negative slope appears everywhere in our daily lives:
Example 1: Downhill Road
As you drive down a hill, your elevation decreases as you move forward. This is a negative slope.
Example 2: Temperature Drop
On a cool evening, the temperature might decrease over time. If we graph temperature vs. time, we'd see a negative slope.
Example 3: Money in Your Wallet
If you spend $5 each day, the money in your wallet decreases over time. The graph of money vs. days would have a negative slope.
Example 4: Slide at Playground
As you move along a slide from top to bottom, your height decreases. This is a perfect example of negative slope!
Think About It
Can you find three more examples of negative slope in your daily life?
Slope Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about negative slope:
Math Trivia
Discover interesting facts about slopes and math:
Ancient Slope Calculations
The concept of slope dates back to ancient Egypt, where builders used slope calculations to construct pyramids. They measured the "seked" - the horizontal distance for a vertical drop of one cubit.
Slope in Science
In physics, slope represents rate of change. Velocity is the slope of a distance-time graph, and acceleration is the slope of a velocity-time graph. Negative slope can indicate deceleration.
Slope in Space Exploration
NASA engineers calculate slopes to design spacecraft landing trajectories. The Mars rovers had to land on surfaces with slopes less than 15 degrees to avoid tipping over.
Steepest Road
Baldwin Street in New Zealand holds the record for the world's steepest residential street with a slope of 35% (about 19.3°). That's a slope of -0.35 - steep enough that it's paved with concrete for better traction!





