Plane in Math - Definition, Examples, Quiz, FAQ, Trivia
Discover the flat world of geometric planes and how they help us understand space!
What is a Plane in Math?

In math, a plane is a flat, two-dimensional surface that goes on forever in all directions. Imagine an endless, perfectly flat sheet of paper with no thickness - that's what mathematicians mean by a plane!
Planes are important in geometry because they help us understand shapes, angles, and how objects relate to each other in space. We use planes to describe the flat surfaces we see in the world around us.
Math Fact!
Any three points that are not in a straight line will always lie on exactly one plane. This is why three-legged stools don't wobble!
Characteristics of a Plane
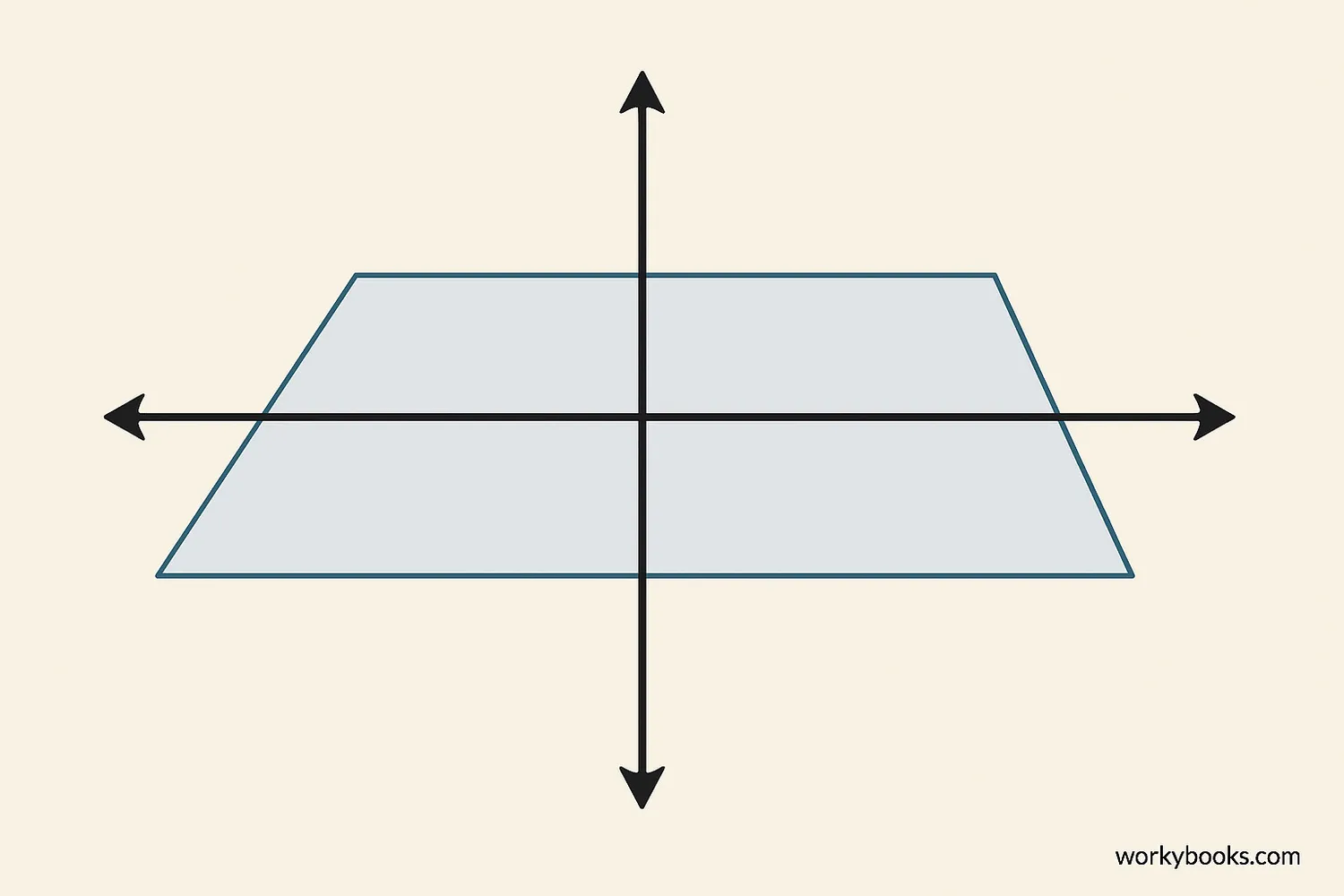
Planes have special characteristics that make them different from other geometric figures:
Flat Surface
A plane is completely flat with no curves or bends
Two-Dimensional
It has length and width but no thickness
Infinite Extension
It extends forever in all directions
No Boundaries
A plane has no edges or boundaries
In diagrams, we often show planes as quadrilaterals (like rectangles or parallelograms), but it's important to remember that these are just representations of the infinite plane.
Plane vs Line
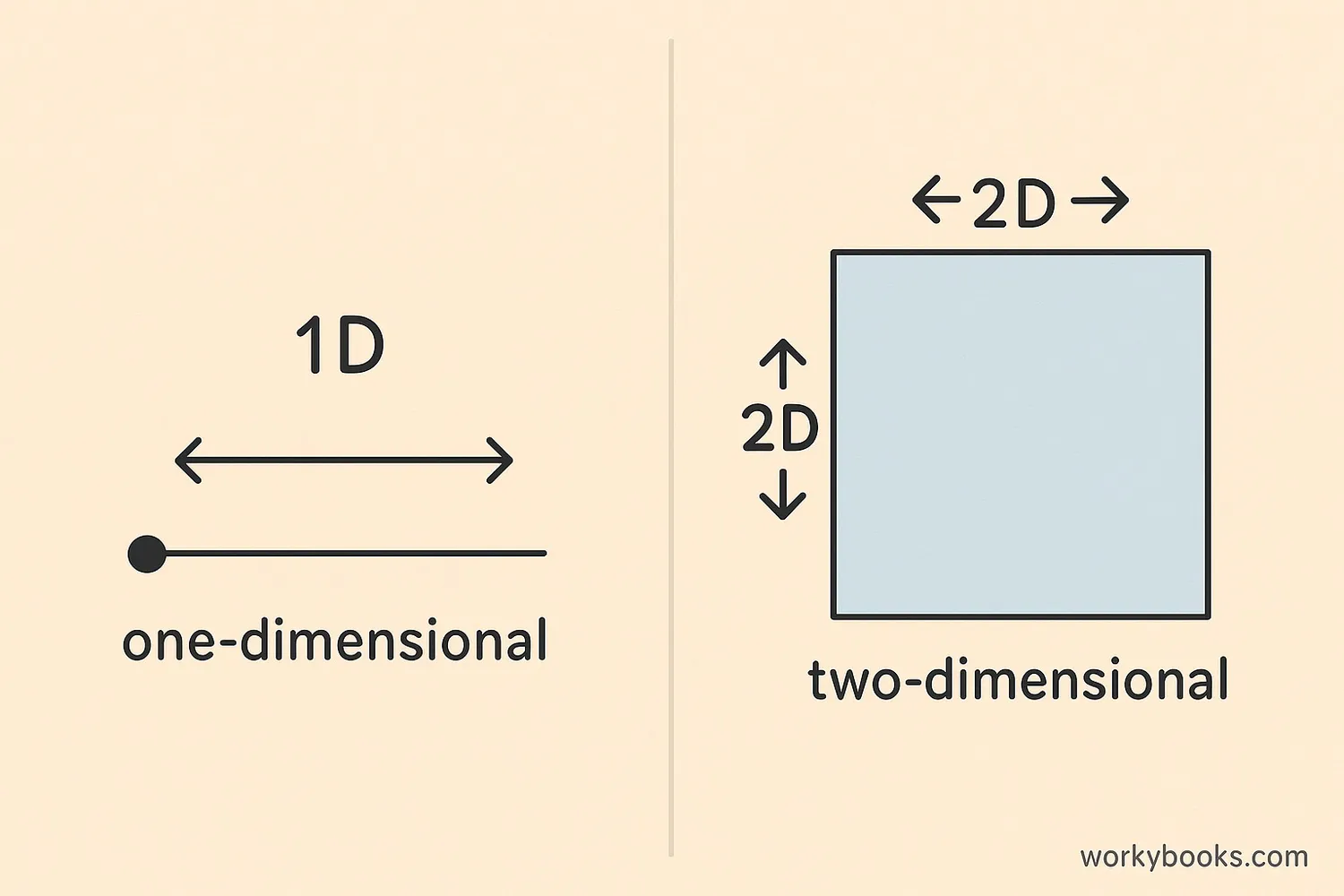
It's important to understand how planes are different from lines in geometry:
| Feature | Line | Plane |
|---|---|---|
| Dimensions | One (length only) | Two (length and width) |
| Extension | Infinite in two directions | Infinite in all directions |
| Thickness | None | None |
| Contains | Points | Points and lines |
| Real-world example | Straight edge of a ruler | Surface of a calm lake |
Remember: A line has only length, while a plane has both length and width. Many lines can lie on the same plane, and when two planes meet, they intersect in a line.
Real World Examples of Planes

While true mathematical planes are infinite, we see parts of planes all around us in everyday life:
Whiteboard
The surface of a whiteboard is part of a plane
Window Pane
A flat window represents part of a plane
Sheet of Paper
A flat piece of paper is part of a plane
Floor Tile
The surface of a floor tile is part of a plane
It's important to remember that these real-world objects are not perfect planes because they have edges and boundaries. But they help us understand what a mathematical plane would be like.
Math Tip!
When you're working with geometry problems, imagine planes as huge, flat surfaces that go on forever. This will help you understand how points and lines can lie on the same plane.
Geometry Quiz
Test your knowledge about planes in geometry with this quiz! Answer all 5 questions to see how much you've learned.
Frequently Asked Questions
Here are answers to some common questions about planes in geometry:
Math Trivia
Discover some amazing facts about planes and geometry!
Ancient Geometry
The concept of a plane was first described by the ancient Greek mathematician Euclid over 2,300 years ago in his book "Elements," which is still considered one of the most influential math books ever written.
Coordinate Planes
The coordinate plane we use in algebra was invented by French mathematician René Descartes. The story says he got the idea while watching a fly crawl on his ceiling!
Beyond Three Dimensions
While we live in a three-dimensional world, mathematicians work with planes in higher dimensions too! Four-dimensional space has hyperplanes that are harder to visualize but follow similar rules.
Video Game Planes
Video game designers use mathematical planes to create 3D environments. When you play a game with a flat surface, like a floor or a wall, it's created using plane geometry!





