Positive Slope - Definition, Examples, Quiz, FAQ, Trivia
Learn about slope in math with simple explanations, real-world examples, and interactive practice
What is Slope?
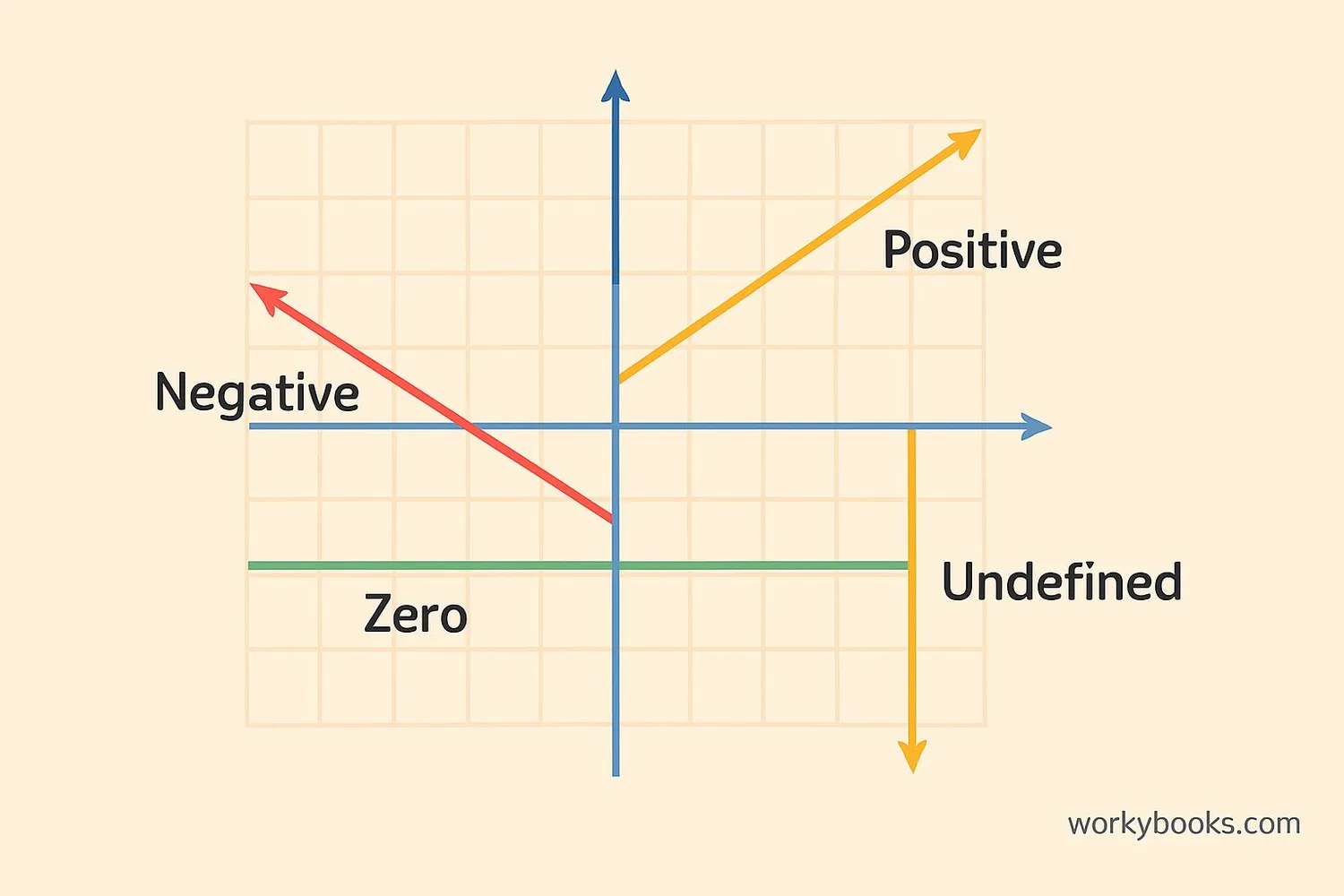
Slope is a measure of how steep a line is. It tells us how much a line rises or falls as we move along it. Slope is an important concept in math that helps us understand and describe lines on graphs.
We calculate slope using the formula:
Slope Formula
Rise is the vertical change (up or down), and run is the horizontal change (left or right).
Positive slope: The line goes upward from left to right
Negative slope: The line goes downward from left to right
Zero slope: The line is completely flat (horizontal)
Undefined slope: The line is completely vertical
Key Concept
Slope measures steepness and direction of a line. Positive slope means the line goes upward as we move to the right.
Understanding Positive Slope
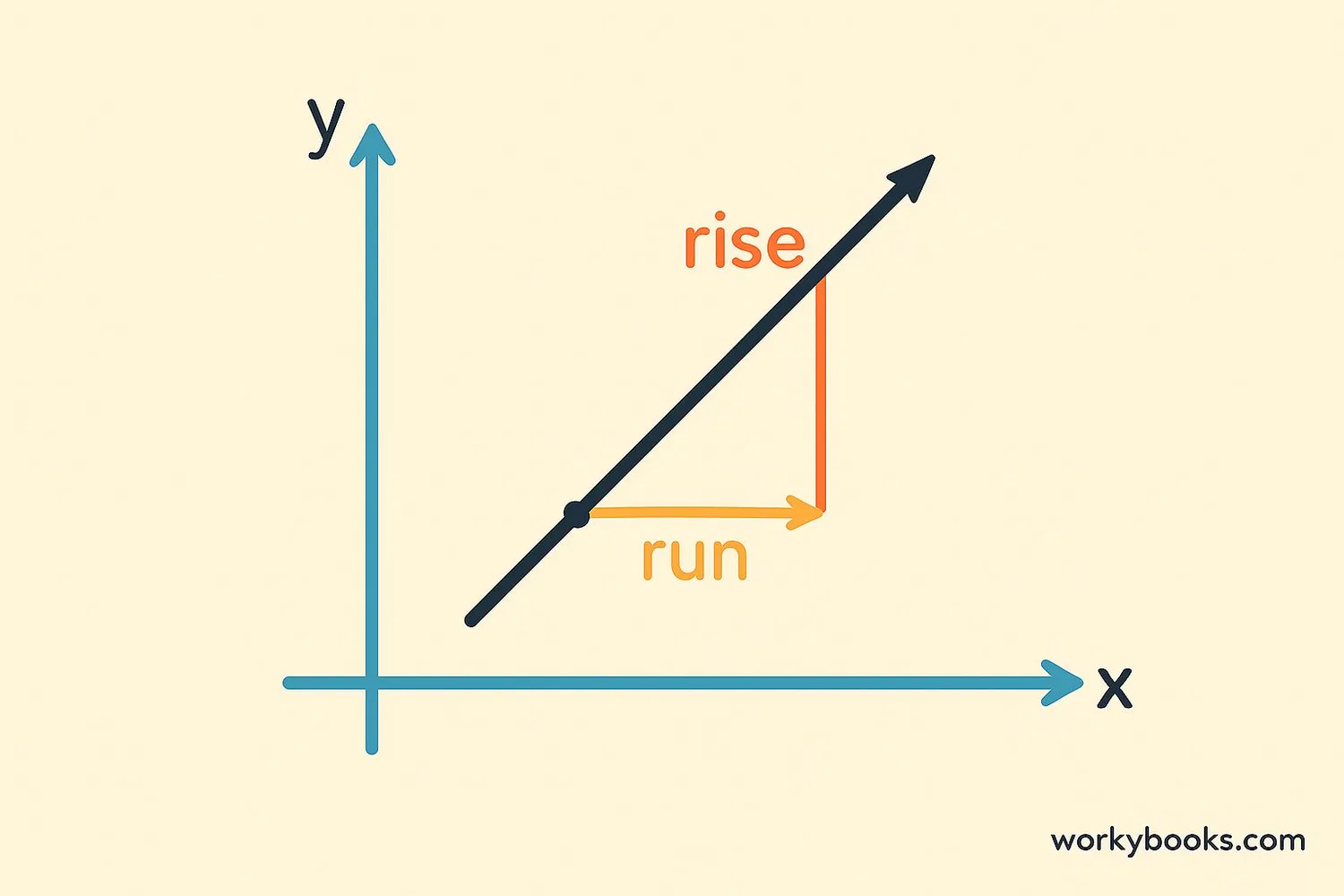
A positive slope means that as we move from left to right along the line, the line goes upward. Think of walking up a hill - that's like a positive slope!
Here's what positive slope looks like:
- When x-values increase, y-values also increase
- The line rises as we move to the right
- The slope value is greater than zero
Examples of positive slope in everyday life:
1. A ramp going upward: As you walk forward (x-direction), you go higher (y-direction)
2. Saving money: The more weeks you save (x), the more money you have (y)
3. Growing plants: The more days pass (x), the taller the plant grows (y)
Remember
Positive slope = ↗️ (upward direction from left to right). If a line goes up as you move to the right, it has positive slope!
Calculating Positive Slope
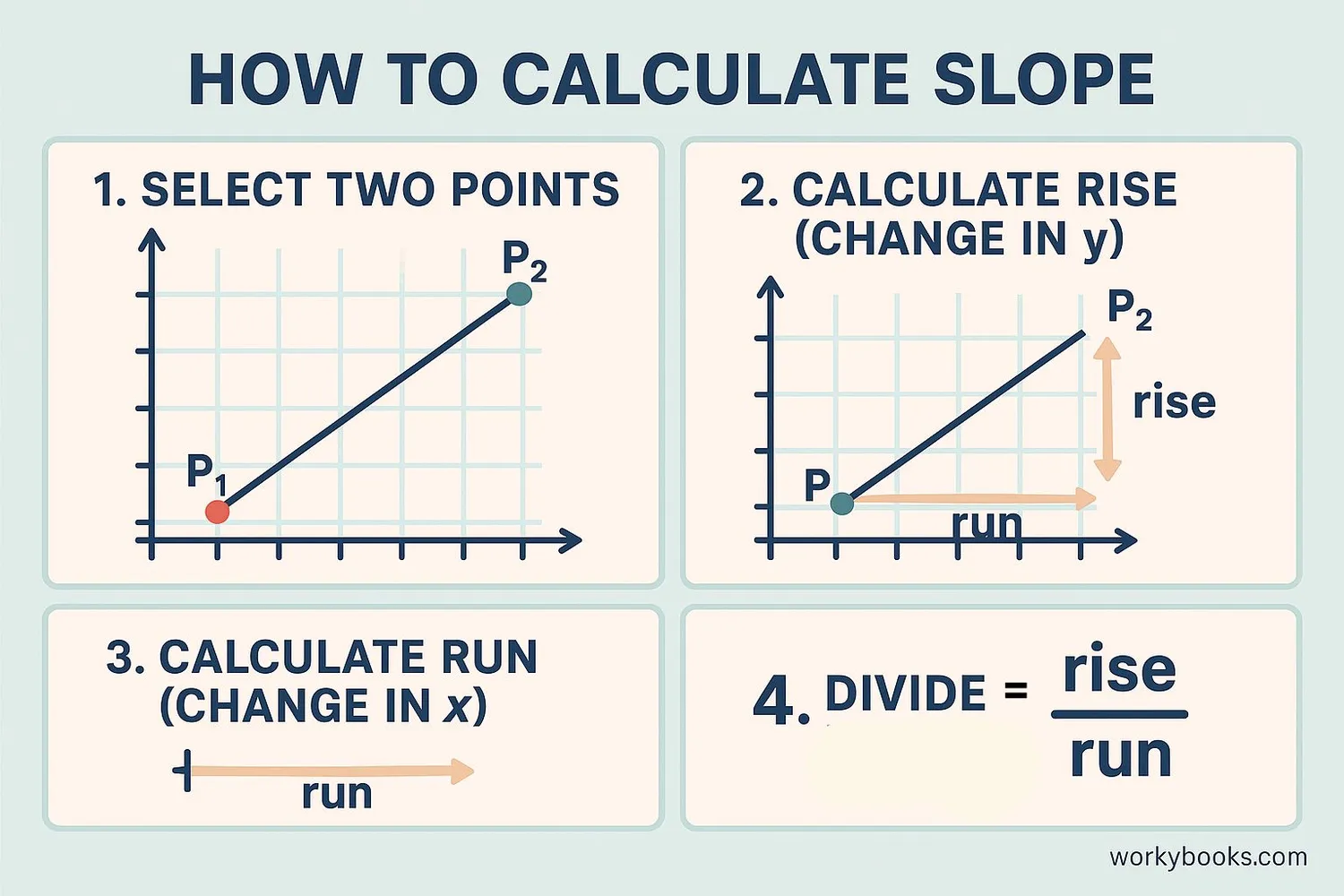
Calculating slope is easy when you remember the formula:
Slope Calculation Formula
Where (x₁, y₁) and (x₂, y₂) are two points on the line.
Example: Find the slope of a line that passes through points (2, 3) and (5, 9)
Step 1: Identify the points → (x₁, y₁) = (2, 3) and (x₂, y₂) = (5, 9)
Step 2: Calculate rise (y₂ - y₁) → 9 - 3 = 6
Step 3: Calculate run (x₂ - x₁) → 5 - 2 = 3
Step 4: Divide rise by run → 6 ÷ 3 = 2
The slope is 2, which is positive! This means the line goes upward as we move to the right.
Try this with different points. Remember: if your answer is positive, the slope is positive!
Slope Tip
When calculating slope, if both rise and run are positive, the slope is positive. If both are negative, the slope is still positive!
Real-World Examples of Positive Slope

Positive slope appears everywhere in our daily lives! Here are some common examples:
1. Staircase or Ramp
As you move forward (run), you also move upward (rise). This creates a positive slope. The steeper the stairs, the larger the slope value.
2. Saving Money
Imagine a graph showing your savings. The x-axis shows weeks, and the y-axis shows money saved. If you save $10 each week, the line will have a positive slope of 10 (rise/run = 10/1).
3. Growing Plants
If you measure a plant's height each day, the graph of height vs. time will have a positive slope. The slope value tells you how fast the plant is growing!
4. Hiking Uphill
When hiking up a mountain, your elevation increases as you walk forward. This creates a positive slope. The steeper the mountain, the greater the slope.
Real-World Tip
Look for situations where two things increase together. If one increases as the other increases, they likely have a positive slope relationship!
Positive Slope Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about positive slope:
Math Slope Trivia
Discover interesting facts about slope:
Ancient Origins
The concept of slope dates back to ancient Egypt, where builders used slope calculations to construct pyramids with precise angles and dimensions.
Steepest Roads
The world's steepest residential street is Baldwin Street in New Zealand with a slope of about 35% (meaning it rises 35 meters for every 100 meters horizontally).
Space Exploration
NASA engineers calculate precise slopes for rocket launch trajectories. A positive slope angle is crucial during liftoff to overcome Earth's gravity efficiently.
Roller Coasters
Roller coaster designers use slope calculations to create thrilling drops. The steepest roller coaster in the world has a 121° drop, which is a negative slope of approximately -5.67.





