Ratios - Definition, Examples, Quiz, FAQ, Trivia
Learn to compare quantities with simple explanations, visual examples, and practice activities
What is a Ratio?

A ratio is a way to compare two or more quantities. It shows how much of one thing there is compared to another thing. Ratios help us understand relationships between different amounts.
For example, if you have 3 apples and 2 oranges, the ratio of apples to oranges is 3 to 2. This means for every 3 apples, there are 2 oranges. Ratios are everywhere in our daily lives - in recipes, maps, and even when sharing things with friends!
Ratios can compare:
- Parts to parts (apples to oranges)
- Parts to whole (apples to total fruits)
- Quantities of the same unit (cm to cm)
- Quantities of different units (miles to hours)
Key Concept
A ratio compares two quantities by division. It tells us how many times one number contains another.
Writing Ratios

Ratios can be written in three different ways. They all mean the same thing!
The ratio formula is:
Ratio Formula
Where 'a' and 'b' are the quantities being compared
Remember
Ratios should always be written in simplest form unless specified otherwise.
Simplifying Ratios
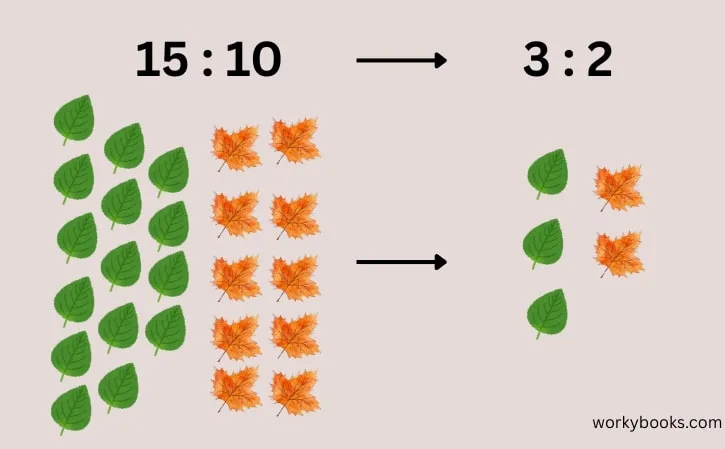
Simplifying a ratio means making the numbers smaller while keeping the same relationship. It's like reducing fractions in math. To simplify a ratio:
- Find the greatest common factor (GCF) of both numbers
- Divide both numbers by the GCF
- Write the simplified ratio
Step 1: The GCF of 18 and 24 is 6
Step 2: 18 ÷ 6 = 3, 24 ÷ 6 = 4
Step 3: The simplified ratio is 3:4
Simplification Tip
If you can't find the GCF, keep dividing both numbers by common factors until you can't divide anymore.
Equivalent Ratios

Equivalent ratios are different ratios that represent the same relationship between quantities. They're like different names for the same thing!
You can create equivalent ratios by multiplying or dividing both parts of the ratio by the same number (just like equivalent fractions).
Example: Find two ratios equivalent to 2:3
Multiply both numbers by 2: 2×2 : 3×2 = 4:6
Multiply both numbers by 3: 2×3 : 3×3 = 6:9
So 4:6 and 6:9 are equivalent to 2:3
You can test if two ratios are equivalent by cross-multiplying:
Is 3:4 equivalent to 9:12?
3 × 12 = 36 and 4 × 9 = 36
Since both products are equal, the ratios are equivalent!
Equivalent Tip
All ratios that simplify to the same basic ratio are equivalent.
Part to Part and Part to Whole Ratios
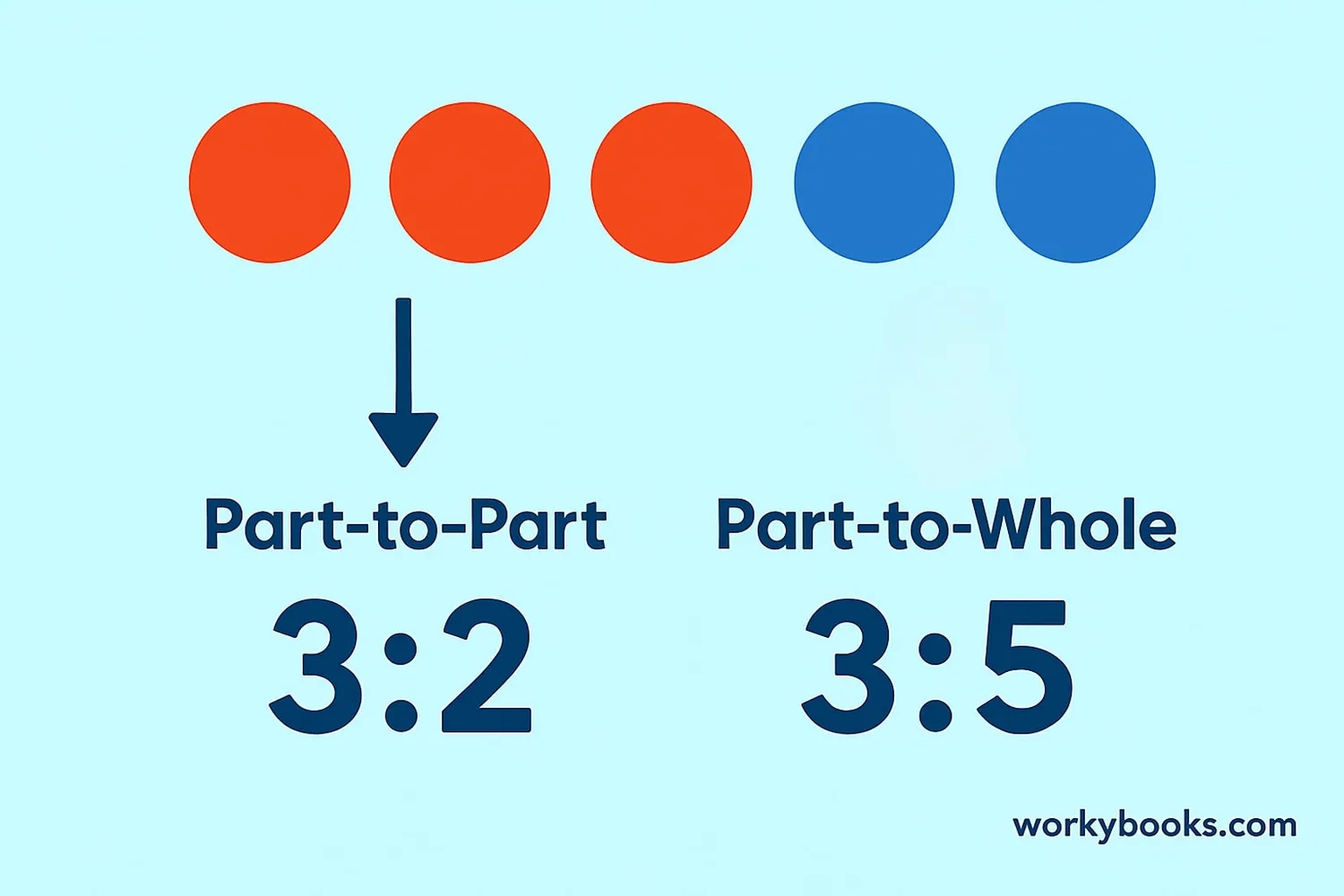
There are two main types of ratios:
Part-to-Part Ratios: Compare one part to another part
Example: In a fruit bowl with 3 apples and 2 oranges, the part-to-part ratio of apples to oranges is 3:2
Part-to-Whole Ratios: Compare one part to the whole group
Example: In the same fruit bowl, the part-to-whole ratio of apples to total fruits is 3:5 (since 3 apples + 2 oranges = 5 fruits)
Understanding the difference helps you solve different kinds of problems:
| Ratio Type | What It Compares | Example |
|---|---|---|
| Part-to-Part | Component to component | Teachers to students |
| Part-to-Whole | Component to total | Teachers to school population |
Ratio Tip
When asked for a ratio, pay attention to whether it should be part-to-part or part-to-whole.
Ratio and Proportion

Proportion is an equation that shows two ratios are equivalent. When two ratios are proportional, they have the same relationship between quantities.
Example: 2:3 = 4:6 is a proportion because both ratios represent the same relationship
There are two special types of proportion:
Direct Proportion: When one quantity increases, the other increases at the same rate
Example: The more hours you work, the more money you earn (if paid hourly)
Inverse Proportion: When one quantity increases, the other decreases
Example: The more workers you have, the less time it takes to complete a job
The Golden Ratio is a special proportion found in nature and art. It's approximately 1.618:1 and appears in seashells, flowers, and famous artworks.
Proportion Tip
You can solve proportion problems by cross-multiplying: a/b = c/d becomes a×d = b×c
Ratio Practice Quiz
Test your ratio knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about ratios:
Ratio Trivia
Discover interesting facts about ratios:
Ancient Ratios
The ancient Egyptians used ratios to build the pyramids. The ratio of a pyramid's height to its base length was carefully calculated.
Nature's Ratios
The Fibonacci sequence (1, 1, 2, 3, 5, 8, 13...) creates ratios that appear in sunflowers, pinecones, and hurricanes!
Golden Ratio in Art
Many famous artworks, like the Mona Lisa, use the Golden Ratio (1.618:1) for composition because it's naturally pleasing to the eye.
Ratio in Music
Musical notes form ratios! A perfect fifth has a frequency ratio of 3:2, and a perfect fourth has a ratio of 4:3.





