Reduction Formulas - Definition, Examples, Quiz, FAQ, Trivia
Learn how to simplify complex integrals with step-by-step explanations and practice activities
What is a Reduction Formula?
A reduction formula is a mathematical tool that helps us solve complex integrals by breaking them down into simpler forms. Think of it like solving a big puzzle by starting with smaller pieces!
Reduction formulas express an integral with a higher power in terms of integrals with lower powers. For example, instead of solving ∫sin⁵(x)dx directly, we can use a reduction formula to express it in terms of ∫sin³(x)dx, which is easier to solve.
These formulas are especially helpful for integrals involving:
- Trigonometric functions (sin, cos, tan)
- Exponential functions
- Logarithmic functions
- Polynomials with high exponents
Key Concept
Reduction formulas help us solve difficult integrals by reducing their complexity step-by-step.
How Reduction Formulas Work
Reduction formulas work by expressing a complex integral in terms of a simpler version of itself. Here's the basic approach:
- Identify the integral that matches a reduction formula pattern
- Apply the formula to express it in terms of a similar integral with a lower exponent
- Repeat the process until you reach a base case that can be easily solved
- Work backward to build the complete solution
General Reduction Formula Pattern
Where In is the integral with power n, and In-1 is the same integral with power n-1.
- Integration by parts
- Trigonometric identities
- Algebraic manipulation
Remember
Each application of a reduction formula reduces the exponent by 1 or 2, bringing us closer to a solvable integral.
Types of Reduction Formulas
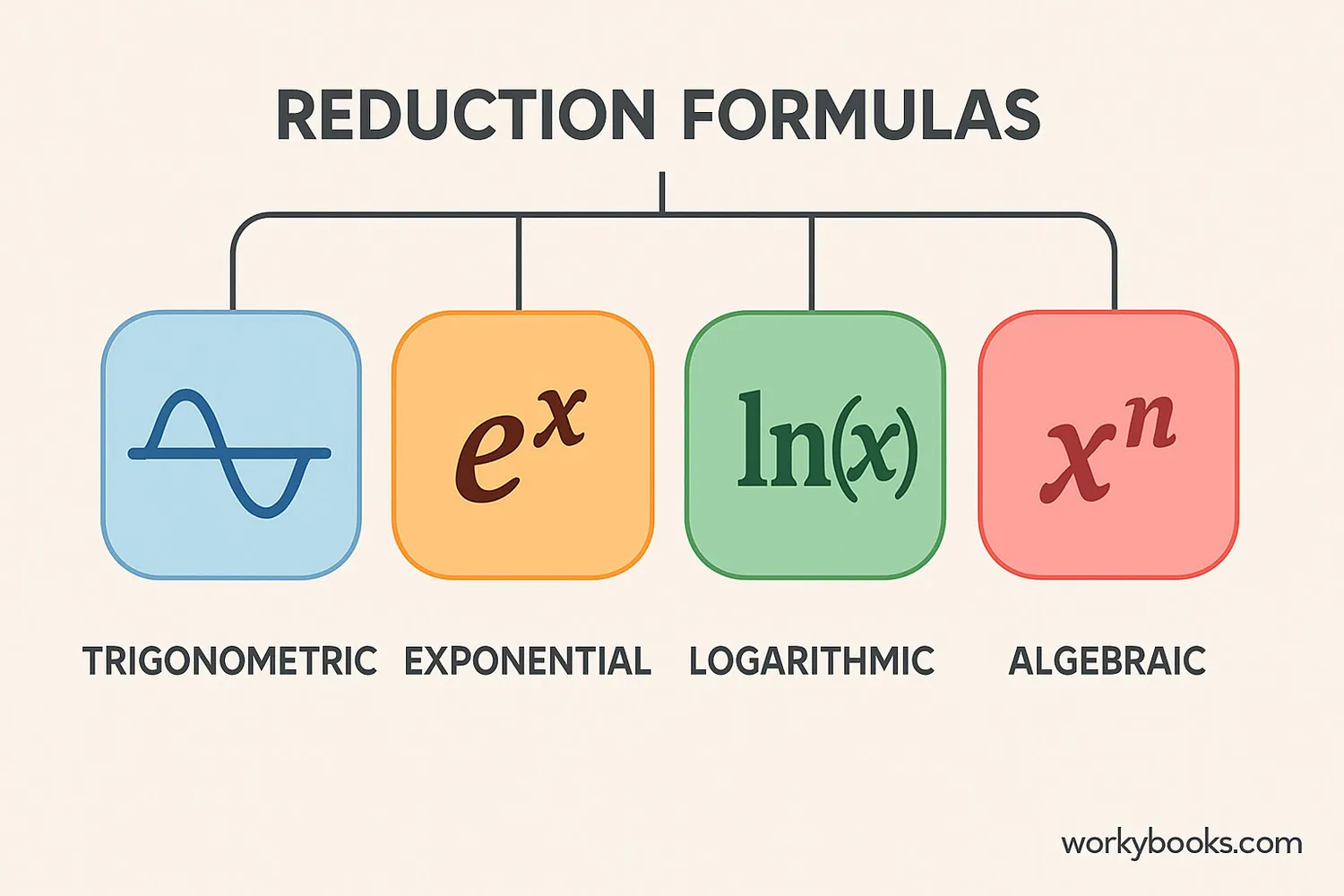
There are several types of reduction formulas for different kinds of integrals. Here are the most common:
Common Reduction Formulas
| Function Type | Reduction Formula |
|---|---|
| Trigonometric (sinnx) | ∫sinnx dx = -1/nsinn-1x cosx + n-1/n∫sinn-2x dx |
| Trigonometric (cosnx) | ∫cosnx dx = 1/ncosn-1x sinx + n-1/n∫cosn-2x dx |
| Exponential (xnemx) | ∫xnemxdx = 1/mxnemx - n/m∫xn-1emxdx |
| Logarithmic (lnnx) | ∫lnnx dx = x lnnx - n∫lnn-1x dx |
| Algebraic (xn(a+bx)m) | ∫xn(a+bx)mdx = ... (varies based on n and m) |
Formula Tip
Notice how each formula reduces the exponent (n) by 1 or 2 with each application.
Real-World Examples
Let's look at some examples of reduction formulas in action:
Example 1: Trigonometric Reduction
Find ∫sin4x dx using reduction formula
Solution:
Step 1: Apply reduction formula for sinnx with n=4
∫sin4x dx = -¼ sin³x cosx + ¾ ∫sin²x dx
Step 2: Apply formula again to ∫sin²x dx
∫sin²x dx = -½ sinx cosx + ½ ∫dx
Step 3: Combine and simplify
Example 2: Exponential Reduction
Find ∫x³exdx
Solution:
Step 1: Apply reduction formula with n=3, m=1
∫x³exdx = x³ex - 3∫x²exdx
Step 2: Apply formula to ∫x²exdx
∫x²exdx = x²ex - 2∫xexdx
Step 3: Continue until you reach ∫exdx
Learning Tip
Start with small exponents (n=2 or 3) to understand the pattern before tackling higher exponents.
Reduction Formula Quiz
Test your understanding of reduction formulas with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about reduction formulas:
Math Trivia
Discover interesting facts about integration and reduction formulas:
Ancient Integration
The concept of integration dates back to ancient Greece. Archimedes used a method similar to integration to calculate areas and volumes around 225 BC, almost 2000 years before calculus was formally developed!
Calculus Creators
Both Isaac Newton and Gottfried Leibniz independently developed calculus in the 17th century. Their rivalry over who invented it first was one of the most famous disputes in mathematics history.
Calculus in Space
NASA engineers use calculus and reduction formulas extensively in space exploration. They help calculate rocket trajectories, orbital mechanics, and spacecraft re-entry angles with precision.
Longest Equation
The longest mathematical equation ever written was for a physics integration problem. When printed, it stretched over 15,000 pages! Reduction formulas help avoid such monstrous calculations.





